机器学习支持向量机(SVM)
svm与logstic异同
? ? ? ?svm支持向量机,因其英文名为support?vector?machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
? ? ? ? svm是一种分类算法,分类算法的起源来自于logstic算法。svm也从logstic延续一些概念如线性分类器和决策边界。然而,svm和logstic在处理非线性问题时,处理方式不同。logstic使用逻辑函数来对数据进行分类,而svm使用核函数来将数据映射到高维空间,以便找到一个超平面来分隔不同类别数据。所以svm在处理非线性数据时有更好的泛化能力和鲁棒性。
最大分类间隔
? ? ??
? ? ? ???超平面方程:
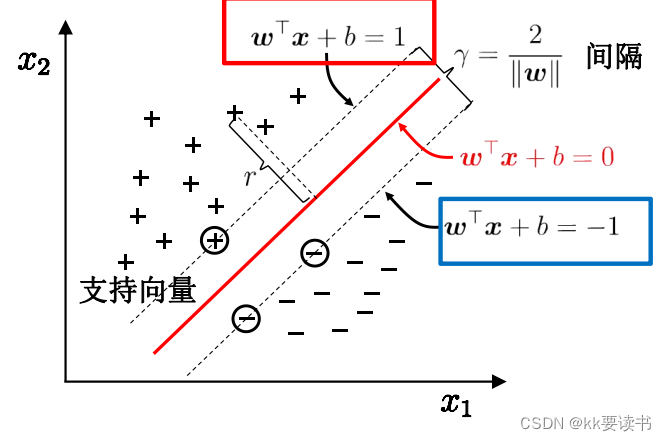




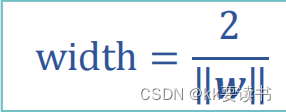
在SVM中,寻找参数w和b的过程可以通过求解以下优化问题来实现:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?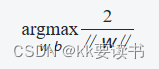
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
其中,xi?表示第i个样本点的特征向量,yi?为其所属的类别(+1或-1),∥w∥表示向量w的模长,b表示偏置项,i=1,2,...,n表示样本的总数。
上述优化问题的目标是最大化分类间隔,即最小化分割超平面到各个类别的最近样本点的距离之和的一半。同时,约束条件要求所有样本点都位于其对应类别的分割超平面的正确侧,即确保分类的正确性。
通过拉格朗日乘子法,可以将上述约束条件转化为以下等价的无约束问题:
?? ? ? ? ? ? ? ? ?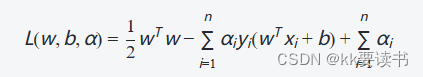
其中,αi?为拉格朗日乘子,用于将原问题转化为对偶问题,并且其取值必须满足αi??0,?i。
接着,可以通过求解argmax?L(w,b,α)来最终确定参数w和b的值,从而得到一个具有最大间隔的分割超平面。
对偶问题
? ? ?
? ? ? ?对于支持向量机(SVM),其对偶问题是将原始问题转化为一个只涉及拉格朗日乘子的优化问题。通过求解对偶问题,可以得到最优的拉格朗日乘子,并进一步计算出最优的参数。
? ? ? ?首先,给定训练样本集D={(x1?,y1?),(x2?,y2?),...,(xn?,yn?)},其中xi?表示输入样本,yi?表示对应的类别标签,且yi?∈{?1,+1}。
? ? ? ?原始问题的目标是找到一个超平面wTx+b=0,使得所有正样本位于超平面上方,负样本位于超平面下方,并且使得间隔最大化。该问题可以表述为以下优化问题:
? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??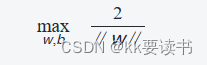
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??![]()
? ? ? ?对于原始问题,引入拉格朗日乘子αi?≥0,得到拉格朗日函数:
? ? ? ? ? ? ? ? ? ? ? ??
? ? ? 然后,使用拉格朗日函数对w和 b求偏导,并令导数为零,可以得到如下的对偶问题:
? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?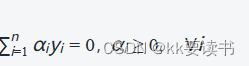
? ? ? 在求解对偶问题时,通过优化拉格朗日乘子αi?,可以求得最优的αi??。然后,通过计算参数w和b,可以得到最优的超平面:
?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??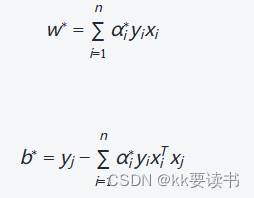
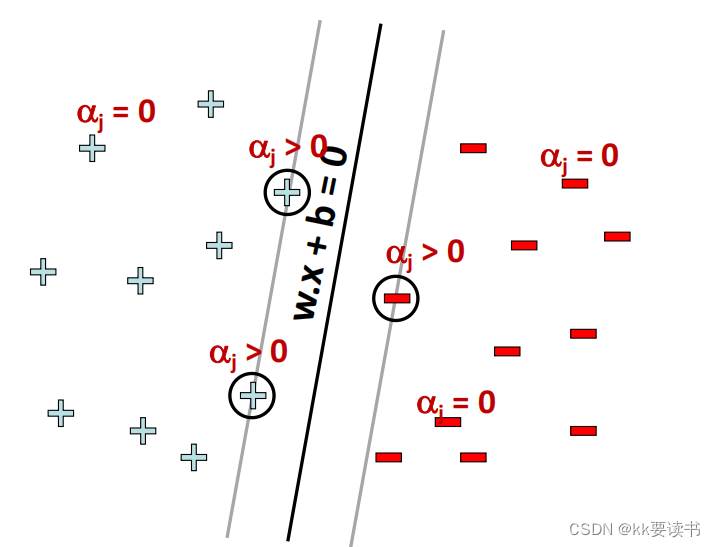
? ? ? ? ?其中,xj?为任意一个支持向量(对应于非零的拉格朗日乘子αj?,yj?为其对应的类别标签。通过求解对偶问题,可以得到最优的拉格朗日乘子,从而确定最大间隔的分割超平面。
?
?核函数
? ? ? ?在支持向量机(SVM)中,核函数是一种用于处理非线性可分问题的技术。它通过将输入样本从原始特征空间映射到一个高维特征空间,使得在高维空间中的样本线性可分或更容易分开。
? ? ? ?核函数的作用是计算两个样本点在高维特征空间中的内积,而无需显式地进行特征向量的计算。这样做的好处是避免了高维特征空间的计算复杂度,而只需在原始特征空间中进行计算。
? ? ? 常用的核函数包括:
-
线性核函数(Linear Kernel):
,它对应于原始特征空间,适用于线性可分的情况。
-
多项式核函数(Polynomial Kernel)
,其中c为常数,d为多项式的次数。它通过引入高阶项,可以处理一定程度上的非线性可分问题。
-
高斯核函数(Gaussian Kernel),也称为径向基函数(Radial Basis Function,RBF):? ? ? ? ? ? ? ? ? ??

? ? ? ? 其中σ为控制高斯核函数宽度的参数。它可以将样本映射到无穷维的特征空间,适用于复杂的非线性可分问题。
? ? ? ?5.Sigmoid核函数(Sigmoid Kernel):,其中α和c为常数。它通常用于神经网络等特定的任务。

软间隔与正则化
? ? ? ?软间隔(soft margin)允许在寻找最优超平面时,允许一些样本点出现在间隔边界上或甚至被错分类。这主要是为了在处理线性不可分问题时保持一定的鲁棒性。软间隔通过引入松弛变量(slack variable),将原始问题转化为一个带有约束的优化问题。
? ? ? ?对于给定的训练样本集D={(x1?,y1?),(x2?,y2?),...,(xn?,yn?)},其中xi?表示输入样本,yi?表示对应的类别标签,且yi∈{?1,+1}yi?∈{?1,+1}。软间隔的目标是找到一个超平面wTx+b=0,使得大部分样本点位于间隔边界以内,并且尽量少的样本点位于间隔边界之外。
优化问题可以表述为以下形式:
? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?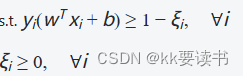
? ? ? ? 其中,ξi?是松弛变量,C是控制错误分类与间隔边界之间权衡的惩罚因子。通过调整参数C的值,可以平衡间隔边界的宽度和错误分类的容忍程度。
? ? ? ? 正则化(regularization)是为了避免模型过拟合而引入的一种技术。在支持向量机中,常用的正则化形式是L2正则化,也称为岭回归。
优化问题可以进一步修改为:
? ? ? ? ? ? ? ? ? ? ? ? ?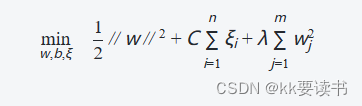
? ? ? ? ? ? ? ? ? ? ? ? ? ? ??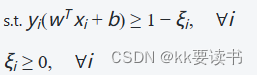
? ? ? ?其中,λ是L2正则化的惩罚系数,用于控制模型的复杂度。较大的λ值会使得模型更加趋向于简单的解决方案,从而减少过拟合的风险。
支持向量回归




代码实现
? ? ? ? 通过支持向量机(Support Vector Machine,SVM)算法对Titanic数据集进行分类预测,代码的目标是根据Titanic数据集中的乘客信息,预测乘客是否生还(1表示生还,-1表示未生还)。
-
loadDataset()函数加载数据集,将数据转换为合适的格式,并进行一些预处理,如删除无关特征、缺失值处理、数据类型转换等。 -
split_data()函数将数据集划分为数据矩阵和标签向量。 -
select_j_rand()函数随机选择另一个待优化的alpha值。 -
clip_alptha()函数修剪alpha值,确保其在指定范围内。 -
smo()函数实现序列最小最优化算法,通过计算误差和优化alpha来求解支持向量。 -
caluelate_w()函数根据求得的alpha值计算权重向量w。 -
prediction()函数进行预测,根据权重向量w和偏置b来判断样本的类别。 -
在
if __name__ == "__main__":下,先加载测试集和训练集,然后调用上述函数进行模型训练和预测。最后统计预测准确率。
1.导入包
import csv
import numpy as np
import matplotlib.pyplot as plt
import copy
from time import sleep
import random
import types2.数据处理
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
if filename != 'titanic.csv':
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][0])
del(data_set[i][2])
data_set[i][4] += data_set[i][5]
del(data_set[i][5])
del(data_set[i][5])
del(data_set[i][6])
del(data_set[i][-1])
category = data_set[0]
del (data_set[0])
# 转换数据格式
for data in data_set:
data[0] = int(data[0])
data[1] = int(data[1])
if data[3] != '':
data[3] = float(data[3])
else:
data[3] = None
data[4] = float(data[4])
data[5] = float(data[5])
# 补全缺失值 转换记录方式 分类
for data in data_set:
if data[3] is None:
data[3] = 28
# male : 1, female : 0
if data[2] == 'male':
data[2] = 1
else:
data[2] = 0
# 经过测试,如果不将数据进行以下处理,分布会过于密集,处理后,数据的分布变得稀疏了
# age <25 为0, 25<=age<31为1,age>=31为2
if data[3] < 25:
data[3] = 0
elif data[3] >= 21 and data[3] < 60: # 但是测试得60分界准确率最高???!!!
data[3] = 1
else:
data[3] = 2
# sibsp&parcg以2为界限,小于为0,大于为1
if data[4] < 2:
data[4] = 0
else:
data[4] = 1
# fare以64为界限
if data[-1] < 64:
data[-1] = 0
else:
data[-1] = 1
return data_set, category
def split_data(data):
data_set = copy.deepcopy(data)
data_mat = []
label_mat = []
for i in range(len(data_set)):
if data_set[i][0] == 0:
data_set[i][0] = -1
label_mat.append(data_set[i][0])
del(data_set[i][0])
data_mat.append(data_set[i])
print(data_mat)
print(label_mat)
return data_mat, label_mat3.SVM
def select_j_rand(i ,m):
# 选取alpha
j = i
while j == i:
j = int(random.uniform(0, m))
return j
def clip_alptha(aj, H, L):
# 修剪alpha
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smo(data_mat_In, class_label, C, toler, max_iter):
# 转化为numpy的mat存储
data_matrix = np.mat(data_mat_In)
label_mat = np.mat(class_label).transpose()
# data_matrix = data_mat_In
# label_mat = class_label
# 初始化b,统计data_matrix的纬度
b = 0
m, n = np.shape(data_matrix)
# 初始化alpha,设为0
alphas = np.mat(np.zeros((m, 1)))
# 初始化迭代次数
iter_num = 0
# 最多迭代max_iter次
while iter_num < max_iter:
alpha_pairs_changed = 0
for i in range(m):
# 计算误差Ei
fxi = float(np.multiply(alphas, label_mat).T*(data_matrix*data_matrix[i, :].T)) + b
Ei = fxi - float(label_mat[i])
# 优化alpha,松弛向量
if (label_mat[i]*Ei < -toler and alphas[i] < C) or (label_mat[i]*Ei > toler and alphas[i] > 0):
# 随机选取另一个与alpha_j成对优化的alpha_j
j = select_j_rand(i, m)
# 1.计算误差Ej
fxj = float(np.multiply(alphas, label_mat).T*(data_matrix*data_matrix[j, :].T)) + b
Ej = fxj - float(label_mat[j])
# 保存更新前的alpha,deepcopy
alpha_i_old = copy.deepcopy(alphas[i])
alpha_j_old = copy.deepcopy(alphas[j])
# 2.计算上下界L和H
if label_mat[i] != label_mat[j]:
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
print("L == H")
continue
# 3.计算eta
eta = 2.0 * data_matrix[i, :]*data_matrix[j, :].T - data_matrix[i, :]*data_matrix[i, :].T - data_matrix[j, :]*data_matrix[j, :].T
if eta >= 0:
print("eta >= 0")
continue
# 4.更新alpha_j
alphas[j] -= label_mat[j]*(Ei - Ej)/eta
# 5.修剪alpha_j
alphas[j] = clip_alptha(alphas[j], H, L)
if abs(alphas[j] - alphas[i]) < 0.001:
print("alpha_j变化太小")
continue
# 6.更新alpha_i
alphas[i] += label_mat[j]*label_mat[i]*(alpha_j_old - alphas[j])
# 7.更新b_1和b_2
b_1 = b - Ei - label_mat[i]*(alphas[i] - alpha_i_old)*data_matrix[i, :]*data_matrix[i, :].T - label_mat[j]*(alphas[j] - alpha_j_old)*data_matrix[i, :]*data_matrix[j, :].T
b_2 = b - Ej - label_mat[i]*(alphas[i] - alpha_i_old)*data_matrix[i, :]*data_matrix[j, :].T - label_mat[j]*(alphas[j] - alpha_j_old)*data_matrix[j, :] * data_matrix[j, :].T
# 8.根据b_1和b_2更新b
if 0 < alphas[i] and C > alphas[i]:
b = b_1
elif 0 < alphas[j] and C > alphas[j]:
b = b_2
else:
b = (b_1 + b_2)/2
# 统计优化次数
alpha_pairs_changed += 1
# 打印统计信息
print("第%d次迭代 样本:%d , alpha优化次数:%d" % (iter_num, i, alpha_pairs_changed))
# 更新迭代次数
if alpha_pairs_changed == 0:
iter_num += 1
else:
iter_num = 0
print("迭代次数:%d" % iter_num)
return b, alphas
def caluelate_w(data_mat, label_mat, alphas):
# 计算w
alphas = np.array(alphas)
data_mat = np.array(data_mat)
label_mat = np.array(label_mat)
# numpy.tile(A, reps):通过重复A给出的次数来构造数组。
# numpy中reshape函数的三种常见相关用法
# reshape(1, -1)转化成1行:
# reshape(2, -1)转换成两行:
# reshape(-1, 1)转换成1列:
# reshape(-1, 2)转化成两列
w = np.dot((np.tile(label_mat.reshape(1, -1).T, (1, 5))*data_mat).T, alphas)
return w.tolist()4.预测
def prediction(test, w, b):
test = np.mat(test)
result = []
for i in test:
if i*w+b > 0:
result.append(1)
else:
result.append(-1)
print(result)
return result5.主程序
if __name__ == "__main__":
test_set, category = loadDataset('titanic_test.csv')
data_set, category = loadDataset('titanic_train.csv')
test_mat, test_label = split_data(test_set)
data_mat, label_mat = split_data(data_set)
b, alphas = smo(data_mat, list(label_mat), 0.6, 0.001, 40)
print(b)
print(alphas)
w = caluelate_w(data_mat, label_mat, alphas)
print(w)
print(test_mat)
print(test_label)
result = prediction(test_mat, w, b)
count = 0
for i in range(len(result)):
if result[i] == test_label[i]:
count += 1
print(count)
print(count/len(result))总结
? ? ? ?支持向量机(Support Vector Machine,SVM)是一种强大的监督学习算法,常用于分类和回归问题,广泛应用于文本分类、图像识别、生物信息学、金融预测等许多领域。
-
优点:
- 在高维空间中有较好的分类性能,适用于复杂的非线性问题。
- 可有效处理小样本情况,具有较好的泛化能力。
- 使用支持向量的形式来表示分类决策函数,因此模型比较简洁。
-
缺点:
- 对大规模训练样本的计算复杂度较高。
- 对参数的选择敏感,需要进行调参。
- 对噪声数据比较敏感,可能导致过拟合。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第19课 SQL入门之使用存储过程
- bootstrap5实现家具品牌商城网站Furniq(电商通用)
- 举个栗子!Tableau 技巧(262):制作渐变色梯度面积图
- Springboot 两种方式配置启动热部署(图文界面)
- C++从零开始的打怪升级之路(day19)
- 【VTKExamples::Visualization】第二期 TestAssignCellColorsFromLUT
- mysql生成数据库字典文档
- 验证码---svg-captcha
- 宠物空气净化器品牌推荐哪个牌子好?五款猫用空气净化器高质量推荐品牌
- I.MX6ULL Linux开发板环境搭建