基于图神经网络的动态物化视图管理

本期 Paper Reading 主要介绍了发布于 2023 年 ICDE 的论文《Dynamic Materialized View Management using Graph Neural Network》，该文研究了动态物化视图管理问题，提出了一个基于 GNN 的模型。在真实的数据集上的实验结果表明，取得了更高的质量。

一、背景

物化视图（Materialized Views，下文简称 MVs）在数据库管理系统中起着至关重要的作用，它通过减少工作负载中共享子查询的冗余计算来提高查询效率。传统方法侧重于静态 MV 管理，它假设不会添加或驱逐 MV。然而，在实际场景中，查询工作负载通常是动态变化的，因此，由于查询分布可能发生变化，以前维护的 MVs 不能很好地适应未来的工作负载。因此，在工作负载动态变化的情况下，研究动态 MV 管理问题是非常重要的。

二、动态 MV 管理的介绍

用于动态工作负载的 MV 的工作机制

动态 MV 管理的两个步骤：

（1）查询重写

给定一个新查询 q，查询重写旨在用当前维护的 MVs 中的一些 MVs 重写 q。为此，这篇论文要估算使用视图 v 回答 q 的好处，即使用 v 后回答 q 的执行时间减少，并选择最能带来好处的 MVs 重写，从而最大限度地提高查询性能。

（2）MV 集合维护

这篇论文考虑一个常见的场景，查询在很长一段时间内连续出现，即动态工作负载。由于查询分布可能发生变化，使用这些固定的 MVs 来优化后续查询的方法不是最优的。因此，这篇论文建议随着新的工作负载的到来，不断迭代地更新 MVs，以应对不断出现的可能的分布转移的查询，这样所有的查询都可以在一段时间内得到很好的优化。

三、动态 MV 管理的介绍

1. 局限

MVs 管理是一个重要的问题，已经研究了几十年。传统的方法利用 DBMS 中的优化器来有效地估计?MVs 的好处，并在此基础上迭代地选择合适的?MVs 来实现。因此，即使在给定新的查询工作负载的情况下从头构建 MV，它们也可以实现高效率，但是由于纯粹使用优化器进行收益估计是不准确的，因此产生了低质量?MV。

为了解决这个问题，基于学习的方法被提出来准确地估计收益。然而，为了处理动态场景，他们必须从头构建?MVs。尽管可以导出高质量的?MVs，但它们昂贵得令人望而却步，因为深度神经架构导致了缓慢的收益/成本估计。因此，在工作负载频繁变化的情况下，它们不能满足高效率的要求。

2. 挑战

要实现在动态场景中最小化查询工作负载的总执行时间的最终目标，有两个基本挑战。首先，在大量查询的情况下，如何准确地估计每个?MV?对每个查询的效益是一个挑战，这对于生成高质量的?MV?具有重要意义。

其次，为了使新的查询能够及时利用生成的?MV，动态场景中的?MV?集维护应该非常高效。但是随着查询数量的增加，如何在保持高精度的前提下有效地进行效益估计是一个很有挑战性的问题。

四、解决方案详述

为了解决这些挑战，这篇论文提出了一个新的框架 GnnMV，利用图神经网络(GNN)来评估效益，以高效和有效的动态?MVs 管理。首先，将动态查询负载维护为查询图，提取并编码查询的关键特征，建立 GNN 模型。其次，为图中的邻居节点设计了一个特征聚集函数，以达到较高的精度。第三，这篇论文提出在由于不断的查询而使图变得越来越大的情况下，提取一个小的子图来进行有效的效益估计。

1. 整体框架介绍

GnnMV 架构

GnnMV 由三个模块组成，即离线 GNN 模型训练、用于查询重写的在线 GNN 推断以及用于?MV?集合维护的 GNN 推断。

最初，这篇论文将历史工作负载作为输入，基于此构建查询图，并在图上训练 GNN 模型，模型的输出是视图对工作负载中查询的益处估计。

接下来，当查询连续在线到达时，训练好的模型用于查询重写和?MV?集维护。给定每个新到达的查询，查询重写模块利用 GNN 模型来估计益处，并且从当前维护的?MV?中选择?MV?来重写查询。

对于新的工作负载，这篇论文生成新的?MV，其中 GNN 模型也被用来估计收益，然后构建二分图用于?MV?选择。

2. GnnMV 的训练

给定收集的用于离线训练的工作负载 WT，通过合并工作负载中查询的查询树来构建查询图。接下来，对图中每个节点的特征（例如，操作符类型、元数据、谓词）进行提取和编码，生成一个特征图。并设计了一个聚合函数来聚合每个节点邻居的特征并生成节点嵌入。

然后，使用查询 q 和视图 v 的嵌入，用一个神经网络计算收益 B’(q，v)。但是物化所有可能的视图太昂贵了，这篇论文对视图进行采样并物化它们（即集合 VT)，用它们优化 WT 中的查询，并计算真正的效益 B(q，v)。然后用 B(q，v)和 B’(q，v)计算损失来训练模型。

（1）特征编码

要建立 GNN 模型，首先要提取图中每个节点的特征并对其进行编码。更具体地说， MVs 管理有三种重要的特性：Operator type、Metadata、Predicate。节点的每个特征向量由这三个特性级联表示。接下来，用一个例子来说明。

如上图所示，设某个节点与 seq-scan 操作符相关联，该操作符扫描谓词为 a.age>30 的 author 表。这篇论文将运算符类型 seq-scan 编码为独热向量 fo(v)，其中 seq-scan 的对应位置具有值 1。谓词 a.age>30 可以表示为表达式树，其中根节点>具有两个子节点 a.age 和 30。这篇论文通过树-LSTM 模型将该表达式树编码为嵌入向量 fp(v)。元数据包含作者、年龄列、扫描成本、行和宽度。这篇论文将其编码到向量 fm(v)中，该向量包含一个独热向量，其中列 a.age 的对应位置具有值 1 和其他统计信息。

（2）效益估计

GNN 模型的最终目标是准确地估计使用物化视图 v 来回答图中的查询 q 的好处(即 B(q，v))。为此，首先要创建训练数据。其次，给定特征编码，这篇论文还需要对查询节点和 MV 节点进行适当的表示（或嵌入），以便模型能够很好地捕捉它们之间的关系，从而准确地估计每个 B(q，v)。

• 训练数据

对 MV 节点的集合进行采样，并将它们物化，因为物化所有可能的视图太昂贵了。对?MV?节点进行统一采样， 这是因为这篇论文要求训练样本是平衡的，以产生具有较强泛化能力的模型。

• 特征传播

视图对查询的好处不仅依赖于其自身的特征，还与其在查询图中的邻居有关。例如，join 操作的成本与其子谓词的选择性高度相关。由于缓冲区的存在，查询的性能与前一个查询有很大的相关性。因此，邻域信息对节点的表示有一定的帮助。

考虑到上述问题，这篇论文采用 GNN 通过图的结构来捕捉不同查询计划之间以及计划节点之间的相关性。这篇论文建议在迭代中传播图上的特征。在每次迭代中，对于每个节点，这篇论文并行聚合其邻居的特征。

GnnMV 中的模型

例如，给定如上图所示的特征图，在第一次传播时，v1 接收 v2、v3、v5、v6 的特征。同时，q1、v7 的特征也被传播到 v6，而 q2、v4 的特征被传播到 v5。然后在第二次传播中，将 v2、v3、v5、v6 再次传播到 v1，但此时 v1 可以捕获 q1 的信息，因为在第一次迭代中，q1 的特征已经传播到 v6。这样，每个节点通过几次迭代就能很好地捕捉到邻居的信息。

• 聚合函数

传播后，需要一个聚合函数来计算每个节点的嵌入，同时考虑节点自身和邻居的特征。一个简单的方法是采用典型的 GCN 聚合器作为聚合函数。具体地说，对于第 k 次传播迭代时的每个节点 v，聚合器计算第 k-1 次迭代时 v 及其邻居的嵌入的元素均值。形式上，

但是，上述方法对每个邻居进行等价处理，没有考虑查询图中不同类型节点和边的不同特征。在查询树中，数据在执行过程中自下而上流动，因此在聚合函数中应该区分父节点和子节点的特性。此外，还应识别子节点的差异。具体地说，这篇论文观察到，如果节点 v 的一个子节点有索引，则 v 中的运算符的执行将比不使用索引更有效，尤其是对于 join 运算符。因此，带或不带索引的子节点将显著影响查询执行。通过分析不同类型节点对效益估计的影响，这篇论文发现为了更好地估计，应该特别对待父节点和索引节点。

针对上述问题，这篇论文设计了一个 MV 聚合器，用于在查询图上进行特征聚合，该聚合器处理父节点、索引节点和其他具有不同线性变换的节点，分别表示为(WF, BF)、(WI, BI)、(WO, BO)。如图 4 所示，依赖于 WF、WI、WO，邻居将在聚合中向节点传播不同的特性。形式上，这篇论文将传播的特性定义为：

MV 聚合函数为：

传播迭代次数为 K，每个节点最终嵌入为e (vi) = hiK

• 效益估计

给定每个节点的嵌入，这篇论文可以估计每个 MV 节点对每个查询节点的好处。通过连接查询 q 和视图v的嵌入，然后是 MLP 来捕获它们之间的关系，然后计算收益 B’(q，v)。假设 q 和 v 分别用 vi 和 vj 表示。形式上:

然后通过最小化损失函数来训练 GNN 模型，目标是优化参数 W 和 b。

3. GnnMV 的推断

（1）查询重写

一旦出现一个新的查询，这篇论文选择 MV 重写查询。首先，这篇论文检测可用的?MV(例如下图中的{v1, v2, v3})。然后，为了选择使回答查询的收益最大化的?MV，需要准确地估计收益。直观的想法是选择那些具有高收益的视图来重写，但是有些视图可能会有冲突，因此不能同时使用。因此，它是一个 NP-hard 问题，选择一个最优的子集与最大的利益，其中每两个视图不冲突。

查询重写和 MV 集维护推理

如上图所示，当 q4 来临时，将它追加到图上，并且 R(q4)={v1,v2,v3}。然后这篇论文的目标是计算 B(q4，v)，λv∈R(q4)。首先提取并编码 q4 的特征，然后这篇论文通过捕捉邻域的特征来计算 e(q4)。假设 k=3，q4 可以捕获离它3跳的节点的信息，即q4的红色节点和查询 q3 和 q2 的黄色节点 v1 和 v3。

在给定的条件下，这篇论文开始选择视图子集去回答查询，因为两个?MVs 可能会相互冲突。因此，它实际上可以表述为一个以节点权值为?MV?收益的加权最大独立集问题，是 NP 难的。这篇论文可以用近似算法来求解它。

（2）MV?集合维护

这篇论文需要周期性地维护?MVs，这样可以进一步适应后续的工作负载。通常，这篇论文根据现有?MVs 的性能触发?MVs 集的维护。这篇论文监视现有?MVs 对最近查询的累积好处，因为好处直接反映了工作负载性能。当累计收益低于阈值时，这篇论文触发 MVs 集维护。

• 效益评估

随着新到达的查询数量的增长，这篇论文派生一个新的工作负载 Wn，将其添加到当前查询图 Wc，并开始维护 MVs 集。为此，这篇论文需要估计?MV?的收益和成本(即候选?MV?的生成成本和现有?MVs 的更新成本)。

成本：通过将执行视图和写入结果的时间相加来估计生成成本，生成成本可以通过从生成视图的已执行查询计划树的子树中提取的信息来计算。这篇论文将更新成本视为?MV?重新计算成本，它大约等于重新创建视图的成本。

收益：为了估计?MV?候选的收益，需要获得节点嵌入。一种简单的方法是对新查询的特征进行编码，在整个图(WC?WN)上传播特征，并推断嵌入。然而，随着大量工作负载的到来，图变得越来越大，整个图的推断非常耗时。而且，没有必要这样做，因为新节点对远离它们的节点在图上的嵌入影响很小。

因此，这篇论文提出在一个提取的子图上计算嵌入，该子图覆盖了必要的特征传播。首先，这个子图肯定包含 WN，因为 WN 中包含的节点的嵌入是未知的。其次，子图还应该包含一些靠近 WN 的节点，因为它们会受到很大的影响，因此它们的嵌入应该更新。

• MV?生成

当新的工作负载到达后，新的当前工作负载变成 Wc=Wc∪Wn。为了在空间预算 τ 内生成优化 WC 的 V*n∈V，这篇论文建立了一个二分图，其中一边的节点来自 WC，另一边的节点来自V。每个边表示 V∈V 到 Q∈WC 的收益，并用 B(q,v)标记。为了考虑视图物化成本，对于创建新视图，这篇论文从创建视图的收益中减去视图物化成本。

有些视图是相互冲突的，在重写查询时，这篇论文使用一个矩阵 T|v|×|v|×w 来表示视图之间的关系，其中 tijk=1(0)表示 vi 和 vj 在 qk 上冲突（不是冲突）。这篇论文使用 xik=1(0)来指示是否选择 vi 重写 qk。这篇论文将 V 的空间表示为|V|，为了获得最大的总收益，这篇论文建模为如下整数规划问题：

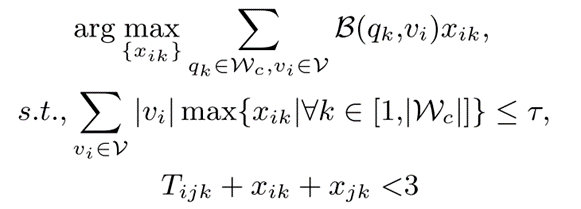
由于这是一个 NP 难问题，这篇论文使用贪婪算法，近似比为 2 来选择 V*。

五、总结

这篇论文提出了一个新的框架 GnnMV，利用图神经网络(GNN)来评估效益，以高效和有效的动态 MVs 管理。

• 首先，将动态查询负载维护为查询图，提取并编码查询的关键特征，建立 GNN 模型；

• 其次，为图中的邻居节点设计了一个特征聚集函数，以达到较高的精度；

• 最后，这篇论文提出在由于不断的查询而使图变得越来越大的情况下，提取一个小的子图来进行有效的效益估计。