（2023，小波变换，度量引导的优化）小波包功率谱 KL 散度：图像合成的新度量

Wavelet Packet Power Spectrum Kullback-Leibler Divergence: A New Metric for Image Synthesis

公众号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

1. 简介

2. 相关工作

2.1. 生成式机器学习

2.2. 生成图像的质量度量

2.3. 生成网络的频率评分

3. 小波功率度量

3.1. 小波功率散度

4. 小波功率散度损失

5. 实验

---

0. 摘要

目前的生成式神经网络度量标准偏向低频率、特定生成器、ImageNet 数据集中的对象，并且更注重纹理而非形状。许多当前的质量度量标准并不直接衡量频率信息。为此，我们提出了一种新的基于频带的质量度量标准，小波包功率谱 KL 散度（D_W）作为图像合成生成方法的质量度量标准，它结合了空间和频率信息。即使我们比较的分布远离 ImageNet 或由不同的生成器架构产生，我们的度量标准也能够很好地工作。我们通过在各种数据集上对广泛选择的生成网络进行抽样来验证我们度量标准的质量。用户研究确保我们的度量标准与人类感知一致。此外，我们展示了频带指导如何改善当前生成网络的频率域保真度。

1. 简介

FID是一个非常有用的度量标准，用于比较相同架构的不同运行，在这种情况下，FID 的降低与人类感知很好地一致[18]。

然而，当用于比较不同架构时，FID 存在重大缺陷，其中一些问题是可以解决的。FID 高度依赖于数据样本的数量 [3]，而用于计算 FID 的高斯假设并不总是成立 [23]。它对调整大小的算法敏感，实现并不总是一致的 [30]，这影响了报告的 FID 分数的可重复性 [30]。例如，图 1 说明了 FID 对由四舍五入引起的图像之间微小差异的敏感性。尽管这三幅图像在感知上相同，但 FID 显示了图像之间惊人的差异。换句话说，FID 可能指示了不存在的差异。当 GAN 与扩散模型进行比较时，这也很重要，因为扩散模型以不同方式钳制 （clamp）输入，这也会影响 FID 分数。

此外，FID分数依赖于 ImageNet 类别，并产生偶然的失真 [18]。如果评估集类似于 ImageNet 类别，或者生成器中使用 ImageNet 权重将输出分布推向 ImageNet，FID 分数会提高。尽管未初始化的随机嵌入不会产生 ImageNet 偏见[27]，但它们并不能解决问题。图 2 说明了一个例子，InceptionV3为 图 2 左边的图像产生了蝴蝶结标签，为右边的图像产生了萨克斯管标签。尽管两幅图像在感知上相似，但错误分类导致左右图像之间的 FID 非常大。中间图像显示了策略性的噪声，经过优化以生成类似于爱因斯坦戴蝴蝶结的优化图。尽管这两幅图像不相似，但两个激活图之间的距离很近，因此 FID 很低。换句话说，相似的图像可能具有较高的 FID，而不相似的图像可能具有较低的 FID。

为了解决 FID 的两个主要缺点，即对小数值差异的高度敏感性和由于使用预训练网络而导致的数据集偏见，我们提出了一种基于小波包变换的替代度量标准。与频率域或空间域中的度量标准不同，小波具有一个优势，即它们结合了空间和频率信息。频率信息很重要，因为生成神经网络具有与真实图像不同的频率偏差 [5]。然而，仅考虑频率信息是不足以评估合成图像的质量的，还需要考虑其他空间信息。因此，小波是比较图像合成的生成方法的度量标准的理想表示。

2. 相关工作

2.1. 生成式机器学习

2.2. 生成图像的质量度量

图像距离度量是评估生成图像质量的一种可能选择。结构相似性指数测量（SSIM）是一种长期存在的图像距离度量 [46]。该得分考虑亮度、对比度和结构。先前的研究报告称 SSIM 偏好模糊图像[37]，这与人类感知不符。在生成机器学习的背景下，[38] 提出了 Inception Score（IS）作为图像质量的度量标准。通过评估 Inception 网络来计算度量标准，找到所有生成图像的标签。对于具有有意义对象的图像，标签熵应该较低，而图像熵应该较高。IS 独立于训练数据集的统计数据。FID通过计算真实图像和合成图像的高级特征的 Wasserstein 距离改进了 IS。今天，使用 FID 分数 [9]比较高级 Inception 网络特征得到了广泛采用。虽然 FID 很好地捕捉了一般趋势，但文献中也讨论了它的缺点。[3] 发现了生成器相关的架构偏见，这限制了它在小于 50,000 图像的较小数据集中比较样本的能力。此外，[30] 发现 FID 对调整大小和压缩非常敏感。[23] 发现 ImageNet 上 Inception 特征的分布是非高斯的。该论文报告了在没有高斯假设的情况下提高稳定性。在比较Tensorflow 和 Pytorch 的实现时，[30] 由于不同的调整大小实现导致了不一致的分数。最后，[16]报告 FID 更注重纹理而不是形状，而人类倾向于相反。总的来说，FID 分数很难复现，除非对其计算的所有细节进行仔细披露 [1]。上述讨论促使我们寻找其他质量度量。

2.3. 生成网络的频率评分

理解和应对当前生成网络倾向于偏向低频和大尺度内容的趋势是一个长期存在的研究问题 [5, 6, 11, 35, 48, 52]。用于理解频率偏差的工具要么是基于傅立叶变换，要么是基于小波变换。小波变换由[24] 和 [4] 首创，在信号处理中有着坚实的记录。快速小波变换（Fast Wavelet Transform，FWT）及其衍生物小波包变换（Wavelet Packet Transform，WPT）在深度学习架构中开始更频繁地出现。应用领域包括卷积神经网络（CNN）增强 [47]，风格迁移 [50]，图像去噪 [21, 39]，图像着色 [20]，人脸老化 [22]，视频增强 [45]，人脸超分辨率 [11] 和生成机器学习 [6,7,33,52]。[8] 使用傅立叶变换来衡量人体运动预测的质量。[52] 使用 Haar FWT 从生成的图像中去除伪影。[33] 侧重于 Haar 小波变换，以提高扩散模型的推理速度。现有工作中绝大多数是基于 Haar 的 [6, 20, 21, 33, 45, 47, 50, 52]。Haar 小波是最简单的选择。[7] 是一个显著的例外，它使用高阶小波。该论文研究了在具有高阶小波的扩散模型中集成 FWT。与小波一起工作的现有技术大多使用 FWT [6, 20, 21, 33, 47, 50]。WPT 在文献中出现的频率较低 [11, 22, 45]。先前使用 WPT 的也通常是基于 Haar 小波的 [11, 45]。

3. 小波功率度量

3.1. 小波功率散度

为了设计一个新的质量度量标准，用于比较图像合成的生成方法，我们需要在领域方面谨慎选择。使用训练网络的特征空间不是一个选项，因为它引入了不必要的评估偏见。基于像素的度量标准偏向低频信息，并偏好模糊的结果 [37]。傅立叶表示不受低频偏见的影响，但它们舍弃了空间信息。例如，倒置生成的对象看起来很奇怪，但使用傅立叶表示的度量不会对其进行惩罚。为了不仅考虑频率，还考虑空间信息，我们提出了一种基于小波包变换（Wavelet Packet Transform，WPT）的度量标准。WPT 递归地过滤输入图像。该变换产生一个频率带表示，结合了空间和频率信息。WPT 计算依赖于四个精心设计的滤波器 a、h、v 和 d，它们允许我们提取谱信息的同时也保留一些空间信息。我们使用五阶 symlet，因为它相对稳定并且具有平衡的滤波权重。虽然我们在补充材料中提供了有关 WPT 的更多细节，但在本节中，我们专注于所提出的基于小波包的质量度量的关键方面。

对于我们的度量标准，我们首先计算图像 I ∈ R^(H×W) 的归一化小波功率谱：

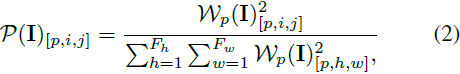
其中，W_p 表示 WPT。指标 i 和 j 表示小波包中的小波包系数，F_h 和 F_w 表示小波包的高度和宽度。p 是来自 P = 4^L 个小波包的小波包的索引，其中 L 表示分解深度。

方程（2）将小波包系数归一化为总和为一，这允许概率解释。在计算了两幅图像 A 和 B 的归一化小波功率谱之后，我们能够测量 KL 散度：?

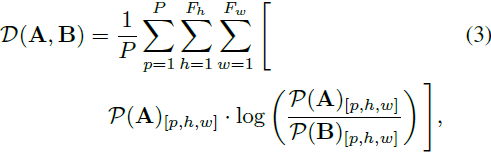
其中，P 表示小波包的总数。对于一组彩色图像，我们在（2）和（3）中添加一个额外的轴，以便batch 轴额外出现在归一化和 KL 散度计算中。我们对通道维度执行相同的操作，这使我们能够处理彩色图像的分布。更正式地说，在这种情况下，我们通过：

在此，b 表示 batch 索引，c 表示通道索引。类似地，?

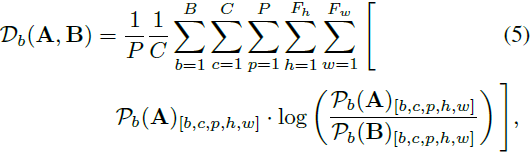
其中，C 表示彩色通道的总数，在我们的情况下为 3。由于 Kullback-Leibler 散度不是对称的，我们通过以下方式定义两幅图像之间的小波包功率谱 Kullback–Leibler 散度（D_W）：?

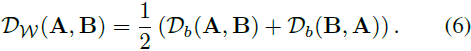
4. 小波功率散度损失

小波包不仅有助于定义度量，而且还可用于训练生成网络，因为它们捕捉空间和频率信息。因此，我们提出了一种小波包引导损失，用于衡量生成图像与目标图像在小波空间中的差异。该损失计算网络输出 ?Y 的小波包表示与期望输出 Y 之间的均方误差（MSE）：

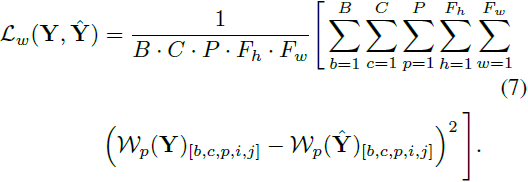
5. 实验

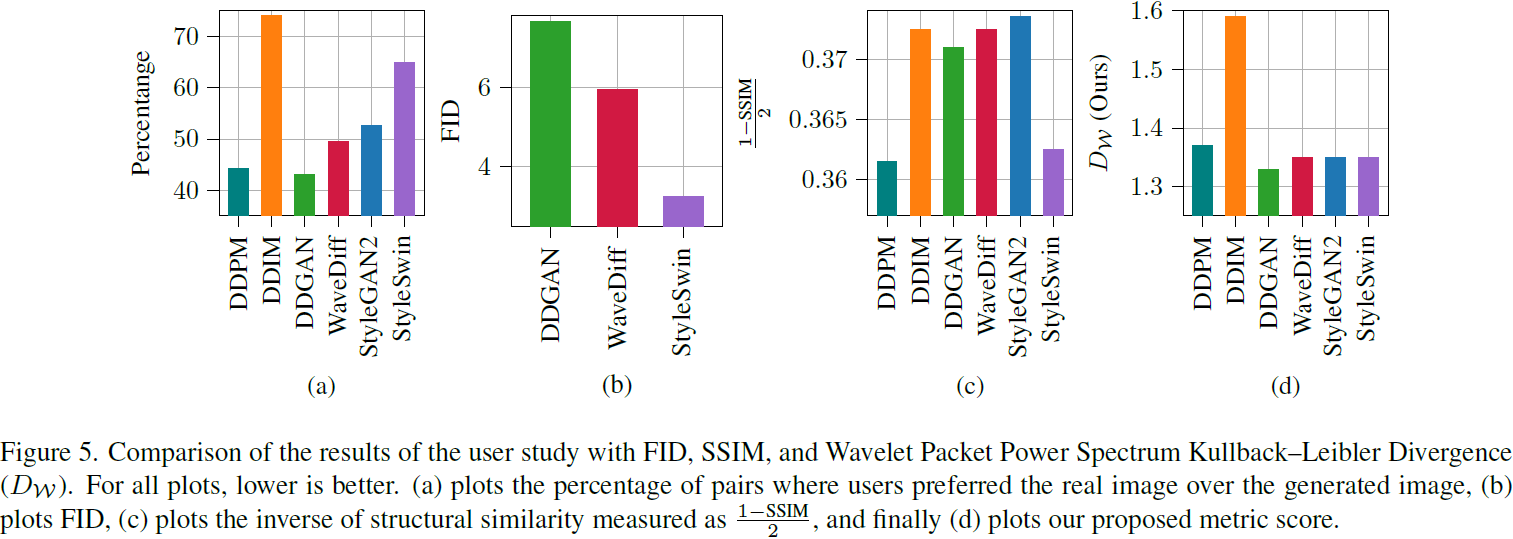
相比于 FID 和 SSIM 指标，使用本文的指标（d）与人类评估结果（a）更为接近。??

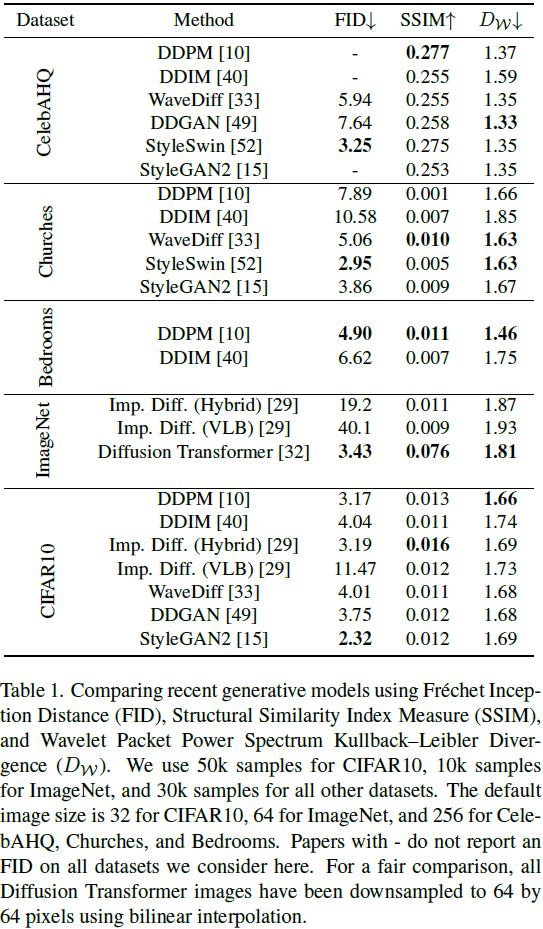
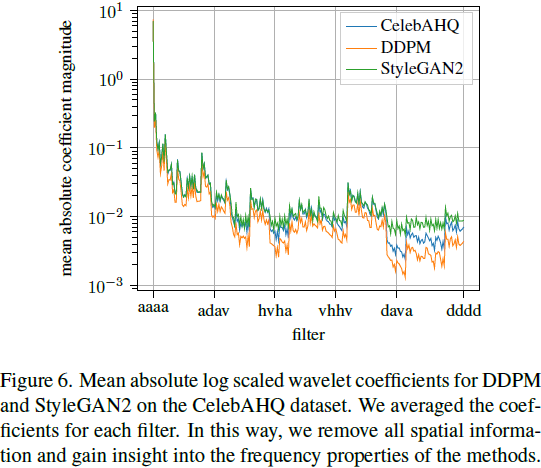
Figure 6 绘制了 CelebAHQ 数据集中的图像以及由 DDPM [10] 和 StyleGAN2 [16] 生成的图像的平均绝对对数尺度小波系数。我们看到 StyleGAN2 的系数更接近真实的 CelebAHQ 频谱，这解释了表 2 中在 CelebAHQ?上 StyleGAN2 的 D_F 分数较低。此外，我们注意到当我们向左移动到更高频率的小波包时，差异增加。?

Figure 7 显示了所有 256 个四级小波包的系数差异。小波包的排列方式是频率沿对角线增加。我们在第四象限看到最大的差异，那里是高频小波包。尽管面部可见，但周围的背景像素似乎更亮。图 7 表明 DDPM 难以正确建模高频背景图样。虽然图 6 已经暗示在较高频率上存在问题，但图 7显示高频错误通常出现在背景中。这也在图 4 中显示的少数示例中可见，其中背景较为平滑。?

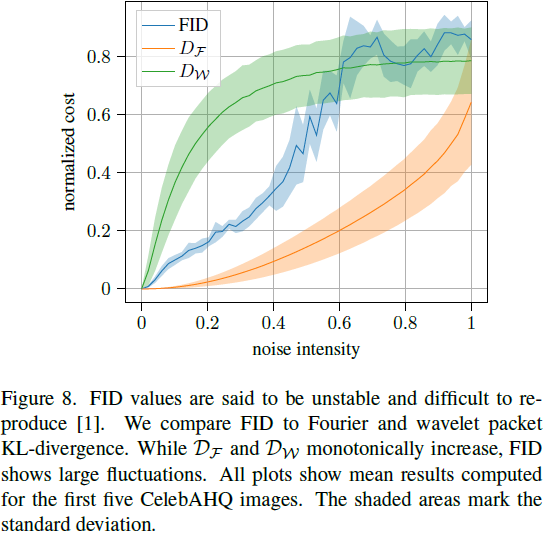
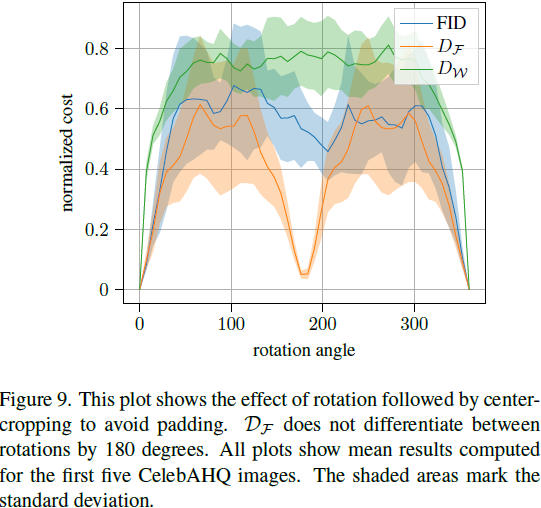
最后，我们研究了向图像添加高斯噪声或旋转图像对 FID、D_F 和 D_W 指标的影响。为此研究，我们使用了 CelebAHQ [13] 的前五幅图像。图 8 绘制了 FID、D_F 和 D_W 对高斯噪声扰动的响应。图表显示 FID 不稳定，在噪声增加时有大幅波动。这种行为是不可取的，使得难以复现结果。D_F 和 D_W 按照预期的方式单调增加。图 9 显示了图像旋转对 FID、D_W 和 D_F 的影响。我们观察到 D_W 对旋转图像产生稳定的误差。FID 表现类似，但显示出较大的波动。然而，基于傅立叶的度量 D_F 不捕捉 180 度旋转，这也证明小波是更好的度量表示。