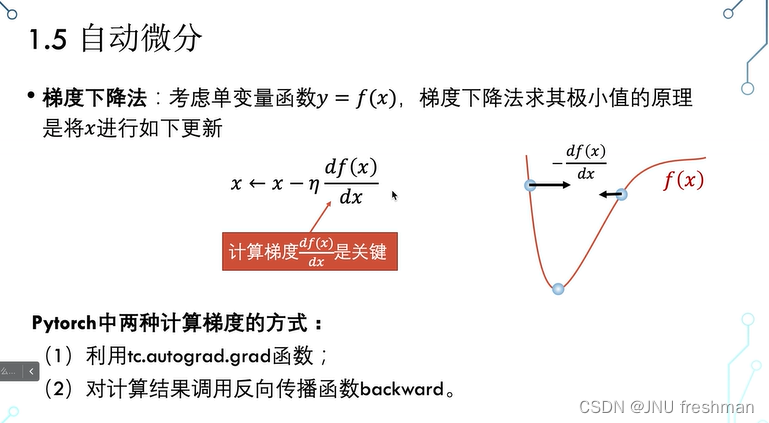
梯度的计算

import torch as tc

# 以函数f(x) = x^2  为例子，求梯度
x1 = tc.tensor(1,dtype=tc.float64,requires_grad=True)
g1 = tc.autograd.grad(x1**2,x1)[0]
print(f"The grad of x**2 at {x1} is {g1}")

(x1 ** 2).backward()
print(f"The grad of x**2 at {x1} is {x1.grad} ")

x2 = tc.arange(3,dtype=tc.float64,requires_grad= True)
g2 = tc.autograd.grad(x2**2,x2,grad_outputs=tc.ones_like(x2) )[0]
print(f"The grad of x**2 at {x2.data} is {g2}")

• 逐一分析代码

当然，让我们逐一分析每一部分代码：

1. 导入 PyTorch 模块

   import torch as tc
   

   这一行导入了PyTorch库，并将其别名设置为tc以方便在代码中使用。

2. 计算梯度例子1

   # 创建一个张量 x1，设置为1，数据类型为float64，并启用梯度追踪
   x1 = tc.tensor(1, dtype=tc.float64, requires_grad=True)
   
   # 使用autograd.grad计算 x1**2 对 x1 的梯度
   g1 = tc.autograd.grad(x1**2, x1)[0]
   print(f"The grad of x**2 at {x1} is {g1}")
   

   这一部分代码创建了一个标量张量x1，并启用了梯度追踪。然后使用autograd.grad计算了函数 x1**2 相对于 x1 的梯度，并将结果打印出来。

3. 计算梯度例子2

   # 使用张量的backward方法计算 x1**2 对 x1 的梯度，并打印结果
   (x1 ** 2).backward()
   print(f"The grad of x**2 at {x1} is {x1.grad}")
   

   这一部分使用了PyTorch中张量的backward方法来计算 x1**2 对 x1 的梯度，并将结果打印出来。这种方式也可以用于计算梯度。

4. 计算梯度例子3

   # 创建一个张量 x2，从0开始，到2结束（不包括2），数据类型为float64，并启用梯度追踪
   x2 = tc.arange(3, dtype=tc.float64, requires_grad=True)
   
   # 使用autograd.grad计算 x2**2 对 x2 的梯度，同时设置grad_outputs为一个与x2相同形状的张量，值都为1
   g2 = tc.autograd.grad(x2**2, x2, grad_outputs=tc.ones_like(x2))[0]
   print(f"The grad of x**2 at {x2.data} is {g2}")
   

   这一部分创建了一个张量x2，该张量包含值从0到2（不包括2）的浮点数，启用了梯度追踪。然后使用autograd.grad计算了函数 x2**2 相对于 x2 的梯度，并设置了grad_outputs参数，最后将结果打印出来。

通过这些注释，你应该能更清楚地理解每一部分代码的作用。