Matlab:isomorphism
发布时间:2024年01月13日
语法:
P = isomorphism(G1,G2) %计算图G1和G2之间的图同构等价关系(如果存在)。若不存在同构,则P为空数组
P = isomorphism(___,Name,Value) %使用一个或多个名称-值对组参数指定其他选项
[P,edgeperm] = isomorphism(___) %返回边置换edgeperm的向量计算同构置换:
示例:
%创建两个有向图G1和G2
G1 = digraph([1 1 1 2 3 4],[2 3 4 4 4 1]);
G2 = digraph([3 3 3 2 1 4],[1 4 2 3 2 2]);
%在画布上绘制两个子图,每个子图显示一个有向图
subplot(1,2,1)
plot(G1)
subplot(1,2,2)
plot(G2)
p = isomorphism(G1,G2)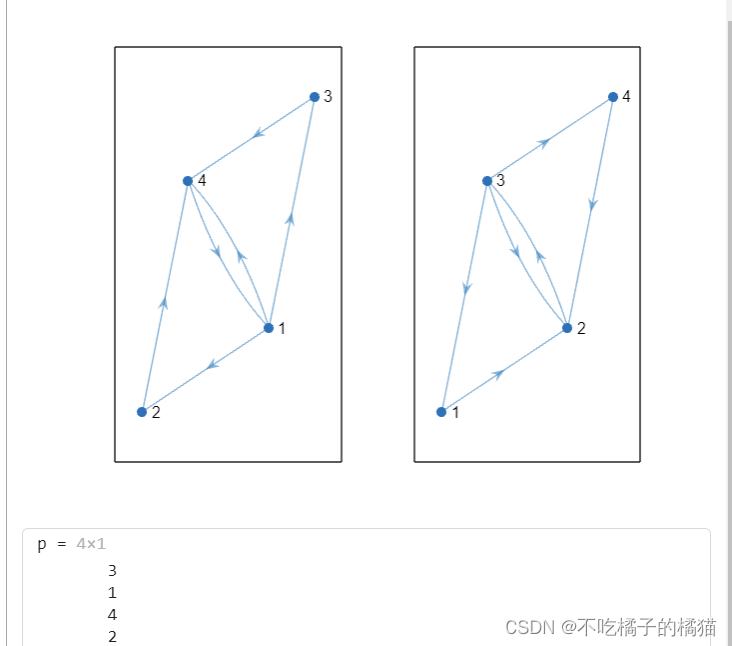
计算具有不同标签和布局的图之间的同构关系:
示例:
%创建并绘制两个图形G1和G2
G1 = graph([1 1 1 2 2 3 3 4 5 5 7 7],[2 4 5 3 6 4 7 8 6 8 6 8]);
plot(G1,'XData',[1 4 4 1 2 3 3 2],'YData',[4 4 1 1 3 3 2 2])
G2 = graph({'a' 'a' 'a' 'b' 'b' 'b' 'c' 'c' 'c' 'd' 'd' 'd'}, ...
{'g' 'h' 'i' 'g' 'h' 'j' 'g' 'i' 'j' 'h' 'i' 'j'});
plot(G2,'XData',[1 2 2 2 1 2 1 1],'YData',[4 4 3 2 3 1 2 1])
%计算两个图之间的同构关系(如果存在)
p = isomorphism(G1,G2)
计算同构关系并保留节点属性:
示例:
%创建一个由3个节点和3条边组成的无向图G1,其中d,e,f分别为三个节点的名称
%e,f,d分别表示三条边的起始节点和终止节点
G1 = graph({'d' 'e' 'f'},{'e' 'f' 'd'});
%设置节点颜色:blue表示节点d的颜色为蓝色,red表示节点e和f的颜色为红色
G1.Nodes.Color = {'blue' 'red' 'red'}';
%创建一个由3个节点和3条边组成的无向图G2,其中a,b,c分别为三个节点的名称
%b,c,a分别表示三条边的起始节点和终止节点
G2 = graph({'a' 'b' 'c'},{'b' 'c' 'a'});
%设置节点颜色:red表示节点a,b的颜色均为红色,blue表示节点c的颜色为蓝色
G2.Nodes.Color = {'red' 'red' 'blue'}';
%在画布上创建一个包含1行2列的子图,并选中第一个子图。该子图用于显示G1。
subplot(1,2,1)
%使用plot函数将无向图G1绘制在第一个子图上,并返回一个plot对象p1
p1 = plot(G1);
%使用 highlight 函数将节点e,f的颜色设置为红色
highlight(p1,{'e' 'f'},'NodeColor','r')
%在画布上创建一个包含1行2列的子图,并选中第二个子图。该子图用于显示G2
subplot(1,2,2)
%使用 plot 函数将无向图G2绘制在第二个子图上,并返回一个plot对象p2
p2 = plot(G2);
%使用 highlight 函数将节点a和b的颜色设置为红色
highlight(p2,{'a' 'b'},'NodeColor','r')
%使用isomorphism函数比较两个无向图G1和G2是否同构
p = isomorphism(G1,G2)
%使用 isomorphism 函数比较两个无向图G1和G2是否同构,并返回比较结果中包含的节点颜色信息
p = isomorphism(G1,G2,'NodeVariables','Color')
%输出一个包含G1节点名称和G2节点名称映射关系的数组
[G1.Nodes.Name, G2.Nodes.Name(p)]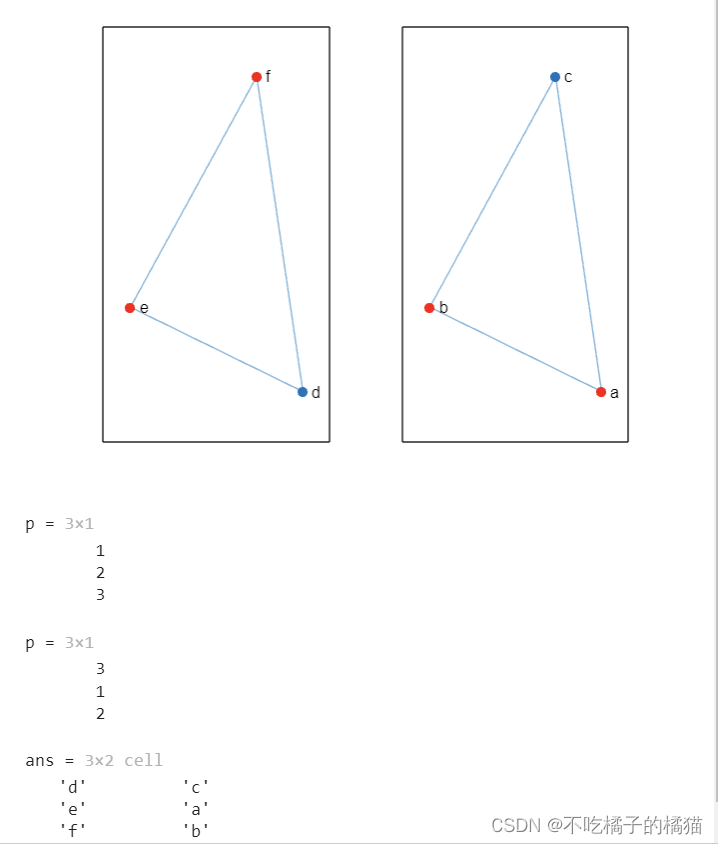
文章来源:https://blog.csdn.net/weixin_73011353/article/details/135566676
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!