2.3 数据链路层03

2.3 数据链路层03

2.3.7 以太网交换机

1、以太网交换机的基本功能

• 以太网交换机是基于以太网传输数据的交换机，以太网交换机通常都有多个接口，每个接口都可以直接与一台主机或另一个以太网交换机相连，一般都工作在全双工方式。

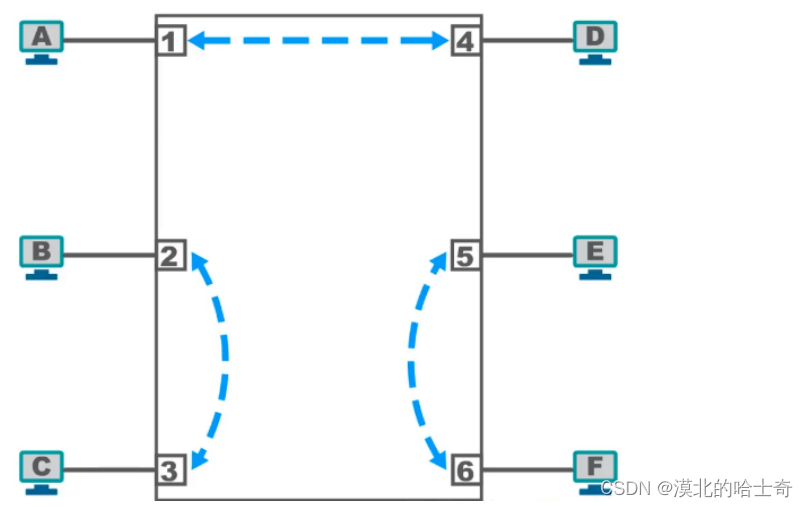
• 以太网交换机具有并行性，能同时连通多对接口，使多对主机能同时通信。
  

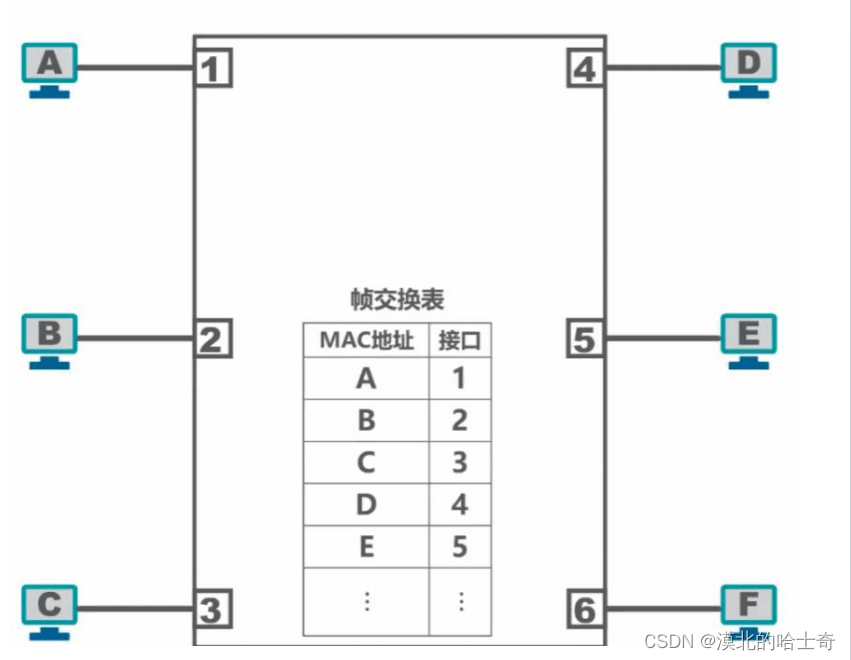
• 以太网交换机工作在数据链路层（也包括物理层），它收到帧后，在帧交换表中查找帧的目的MAC地址所对应的接口号，然后通过该接口转发帧。
  假设主机A想向主机B发送帧，交换机收到A发出的帧后，在帧交换表中查找BMAC地址对应的接口号，然后通过该接口转发帧。
  

• 帧的两种转发方式：

  • 存储转发：交换机在转发之前必须接收整个帧，并进行错误校检，如无错误再将这一帧发往目的地址。帧通过交换机的转发时延随帧长度的不同而变化。
  • 直接交换：采用基于硬件的交叉矩阵（交换机只要检查到帧头中所包含的目的地址就立即转发该帧，而无需等待帧全部的被接收，也不进行错误校验。由于以太网帧头的长度总是固定的，因此帧通过交换机的转发时延也保持不变。)

• 以太网交换机是一种即插即用设备，其内部的帧交换表是通过自学习算法自动的逐渐建立起来的。

2、以太网交换机自学习和转发帧的流程

刚上电时以太网交换机内部的帧交换表是空的，随着网络中各主机间的通信，通过自学习算法自动的逐渐建立起来帧交换表。

如下图所示相互连接的“以太网交换机1”和“以太网交换机2”各自连接了三台主机，构成了一个交换式以太网。为了简单起见各台主机的MAC地址我们用一个对应的大写字母表示，并且假设各台主机知道网络中其他各主机的MAC地址。

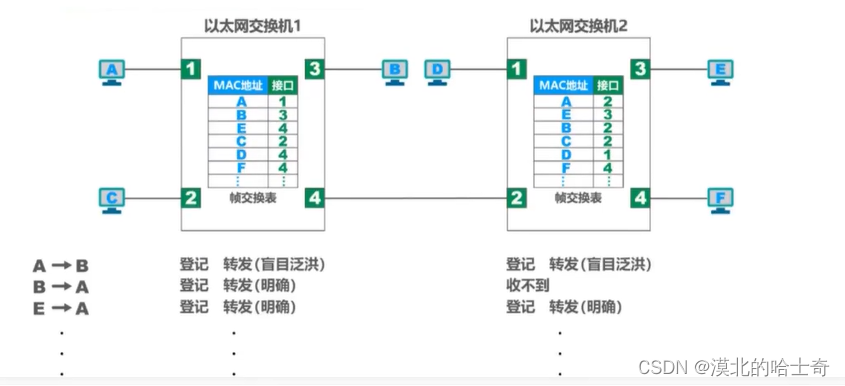
下面我们来了解以太网交换机是如何进行自学习和转发帧的：

• 主机A发送数据给主机B
  • 该帧从交换机1的接口1进入交换机，交换机1首先进行登记工作，将该帧中的源MAC地址A记录到自己的帧交换表中，并且将接口号1与MAC地址A相对应也记录到帧交换表中。以上的登记工作就称之为交换机的自学习。
  • 交换机1对该帧进行转发，该帧中的目的MAC地址是B，在帧交换表中查找MAC地址B，发现找不到就对该帧进行盲目地转发（也成为泛洪），也就说会将该帧在除接口1以外的其他所有接口进行转发。
  • 主机B在接收到该帧后，根据该帧的目的MAC地址B与自己的MAC地址比较，发现相等就说明该帧是发送给自己的，于是主机B接受该帧，主机C则会丢弃该帧。
  • 该帧从交换机1的接口4通过交换机2的接口2进入交换机2，交换机2首先进行登记工作，将该帧中的源MAC地址A记录到自己的帧交换表中，并且将接口号2与MAC地址A相对应也记录到帧交换表中。
  • 交换机2对该帧进行转发，该帧中的目的MAC地址是B，在帧交换表中查找MAC地址B，发现找不到就对该帧进行盲目地转发（也成为泛洪），也就说会将该帧在除接口2以外的其他所有接口进行转发。
  • 主机D、E、F丢弃该帧。
    

注意：在帧交换表中每条记录都有自己的有效时间，到期自动删除。这是因为MAC地址与交换机接口的对应关系并不是永久性的 (对应的接口可能会更换计算机)

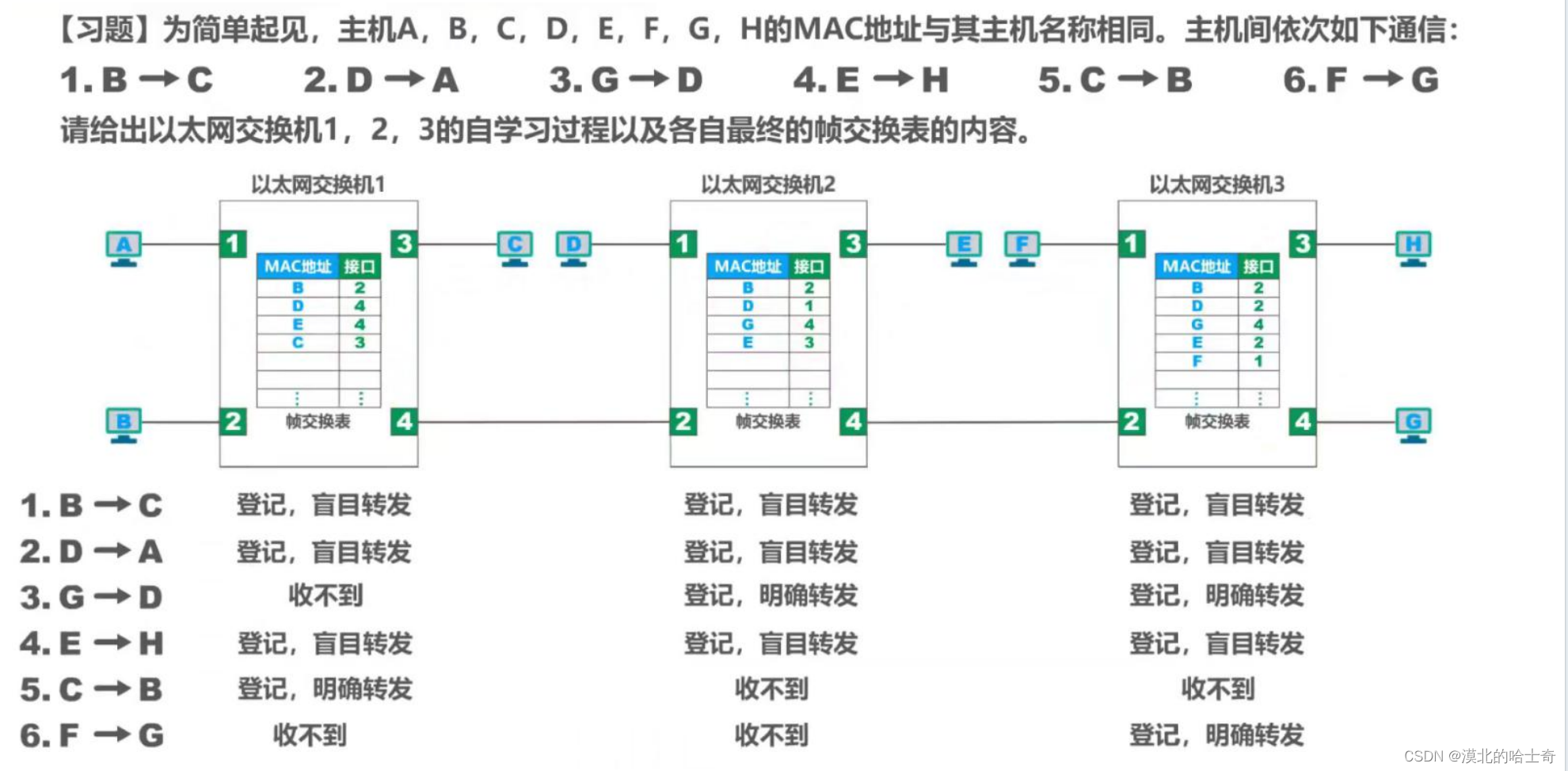
3、以太网交换机的生成树协议STP

• 思考：如何提高以太网的可靠性？假如在网络中有三台交换机A、B、C，他们之间的连接方式如下图所示，假如他们之间的链路出现了故障则会影响各个交换机之间的通信。
  

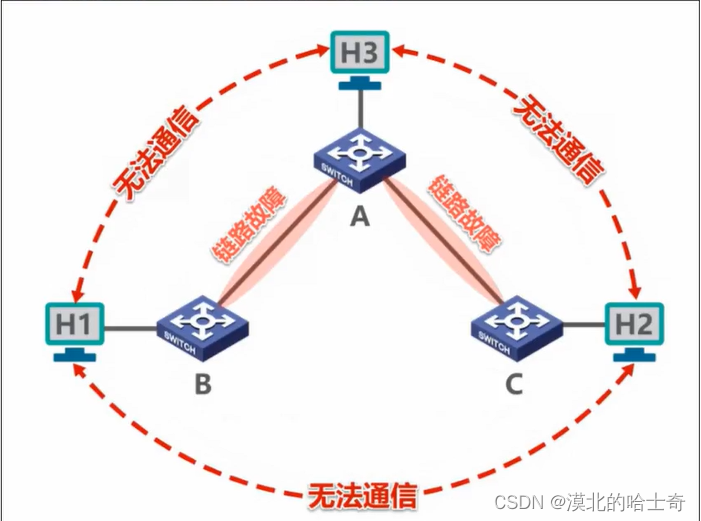
• 添加冗余链路可以提高以太网的可靠性：在交换机B和C之间添加冗余链路。但是余链路也会带来负面效应----形成网络环路
  

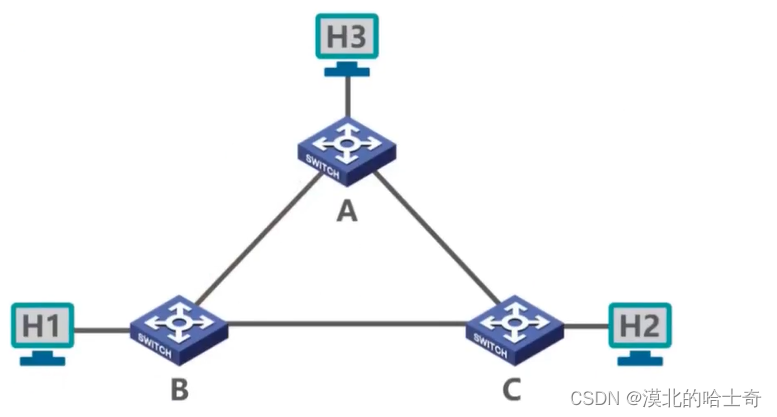
• 网络环路带来的问题：

  • 广播风暴：广播帧在各个交换机之间反复转发，分别按顺时针和逆时针方向同时兜圈。广播风暴会大量消耗网络资源，使得网络无法正常转发其他数据帧。
  • 主机收到反复的广播帧，会大量消耗主机的资源
  • 交换机的帧交换表震荡：同一个MAC地址的记录在其他错误记录之间反复震荡。
    

• 以太网交换机使用生成树协议STP(Spanning Tree Protocol)可以在增加冗余链路来提高网络可靠性的同时又避免网络环路带来的各种问题。

  • 不论交换机之间采用怎样的物理连接，交换机都能够自动计算并构建一个逻辑上没有环路的网络，其逻辑拓扑结构必须是树型的（无逻辑环路)。最终生成的树型逻辑拓扑要确保连通整个网络。
  • 当首次连接交换机或网络物理拓扑发生变化时(有可能是人为改变或故障)，交换机都将进行生成树的重新计算。
    

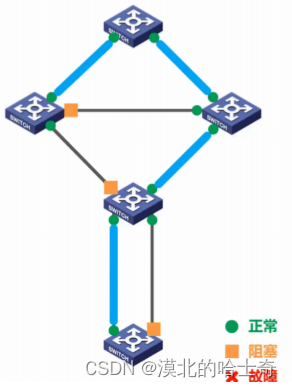
生成树算法STA可自行了解