算法回忆录——排序

1. 插入排序

分为两个序列，前面一个序列是排好序的，后面一个序列是未排好的。未排好的序列的第一个元素（a）从后往前去和排好序的序列的元素（b)挨个比较。若a<b，就需将b往后移一位（需要提前用一个变量存储a的值）。然后继续比较，那么就会有两种情况：1. 比较到a>b时停止，此时a停留的下标就在b的后一个，也就是a要占据的位置。2. 比较到最后也没有比a小的b，此时a就应该占据该有序序列的第一个位置。

a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]


for i in range(1, len(a)):
    # i表示未排好的序列的第一个元素的下标
    # j表示已排好的序列的最后一个元素的下标
    j = i - 1

    # 开始将a[i]与已排好的序列进行比较
    while j >= 0:
        # 如果小于
        if a[i] < a[j]:
            # 下标减一继续往前比较
            j -= 1
        else:
            # 如果a[i] > a[j]，则可以终止循环了
            break
    
    # 循环结束时的j表示a[i]>a[j]的那个j，所以a[i]要放入的位置应该在a[j]的后面
    # 或者说循环结束时一直没有找到比a[i]小的a[j]，此时j为-1，应当放入最前面
    j += 1

    # 将a[i]存储起来
    b = a[i]
    # 然后将已排好的序列从j的位置开始，整体往后移一位
    for n in range(i, j, -1):
        a[n] = a[n - 1]
    # 最后再在j处放上a[i]
    a[j] = b
    
print(a)

改进：可以不用在找到插入位置的时候再挨个往后移，可以先将a[i]存储起来，在与排好的序列挨个比较时就开始往后移。

a = [21, 3, 10, 33, 9, 22, 34, 18, 26, 15, 100, 2, 11, 31, 100, 52]

for i in range(0, len(a) - 1):
    # 排好序列的最后一个元素的下标
    end = i
    
    # 存储好当前未排元素
    wait = a[end + 1]
    
    # 将该未排元素开始依次从后往前与排好的元素比较
    while end >= 0:
        # 如果该未排元素小于当前已排好的元素，就将当前已排好元素往后移
        if wait < a[end]:
            a[end + 1] = a[end]
            end -= 1
        else:
            break
    
    a[end + 1] = wait

print(a)

2. 选择排序

先找到最小的元素，与原序列第一个元素交换，然后再去排除第一个元素的序列中找到最小的，与原序列中第二个元素交换…

a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def select_sort(a, n):
    # 依次从未排序的序列中找到最小的元素的下标
    for i in range(n):
        pos = i
        # 用原序列第一个元素去跟剩下元素比较，找到最小的元素，然后记录下标
        for j in range(i + 1, n):
            if a[j] < a[pos]:
                pos = j
        # 此时已经找到最小元素的下标，与原序列第一个元素交换位置
        a[i], a[pos] = a[pos], a[i]

    return a
print(select_sort(a, len(a)))

3. 冒泡排序

冒泡排序就是将一个数与其它数挨个比较，在比较的过程中，始终是小的数在前面，大的数在后面，这样不断比较和交换，大的数就挨个排到后面去了。

a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def bubble_sort(a, n):
    for i in range(n):
        for j in range(n - 1):
            if a[j + 1] < a[j]:
                a[j], a[j + 1] = a[j + 1], a[j]
    return a
print(bubble_sort(a, len(a)))

4. 希尔排序

希尔排序也算是一种插入排序，不过它是按照某种规则进行分组后，在每个组内进行插入排序。

分组主要就是靠**“增量”**来划分。增量的取值又很多种，普遍简单的是以第一个增量为，数组长度的一半（向下取整），第二个增量取第一个增量的一半…最后一个增量一定是1。

那么是如何按照增量分组的呢？

如果以取半的方式来获得增量，那么有增量是多少，就分多少组。

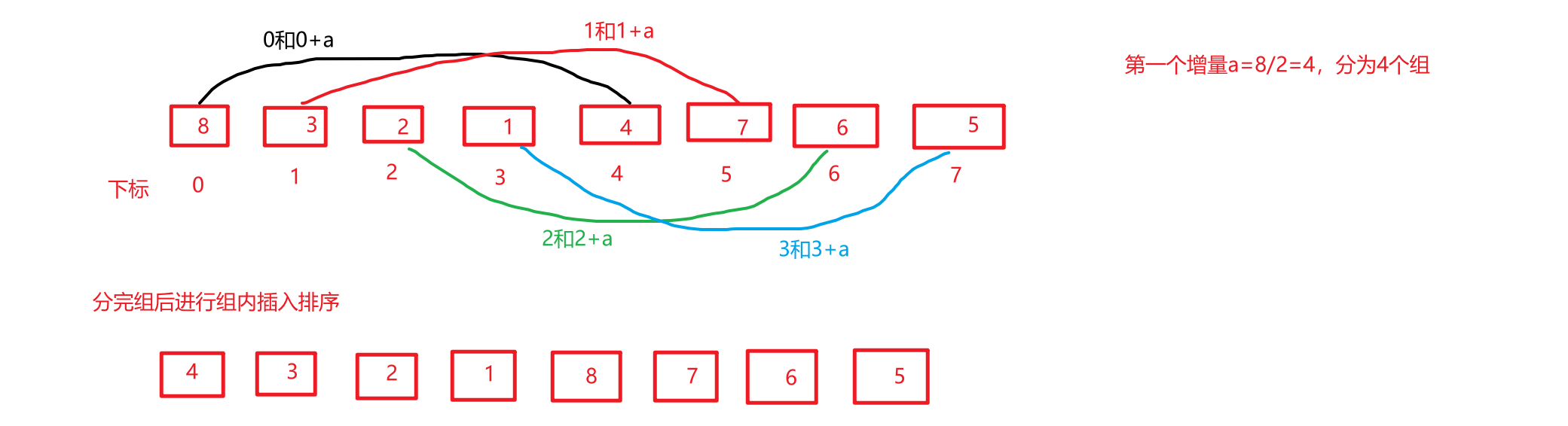
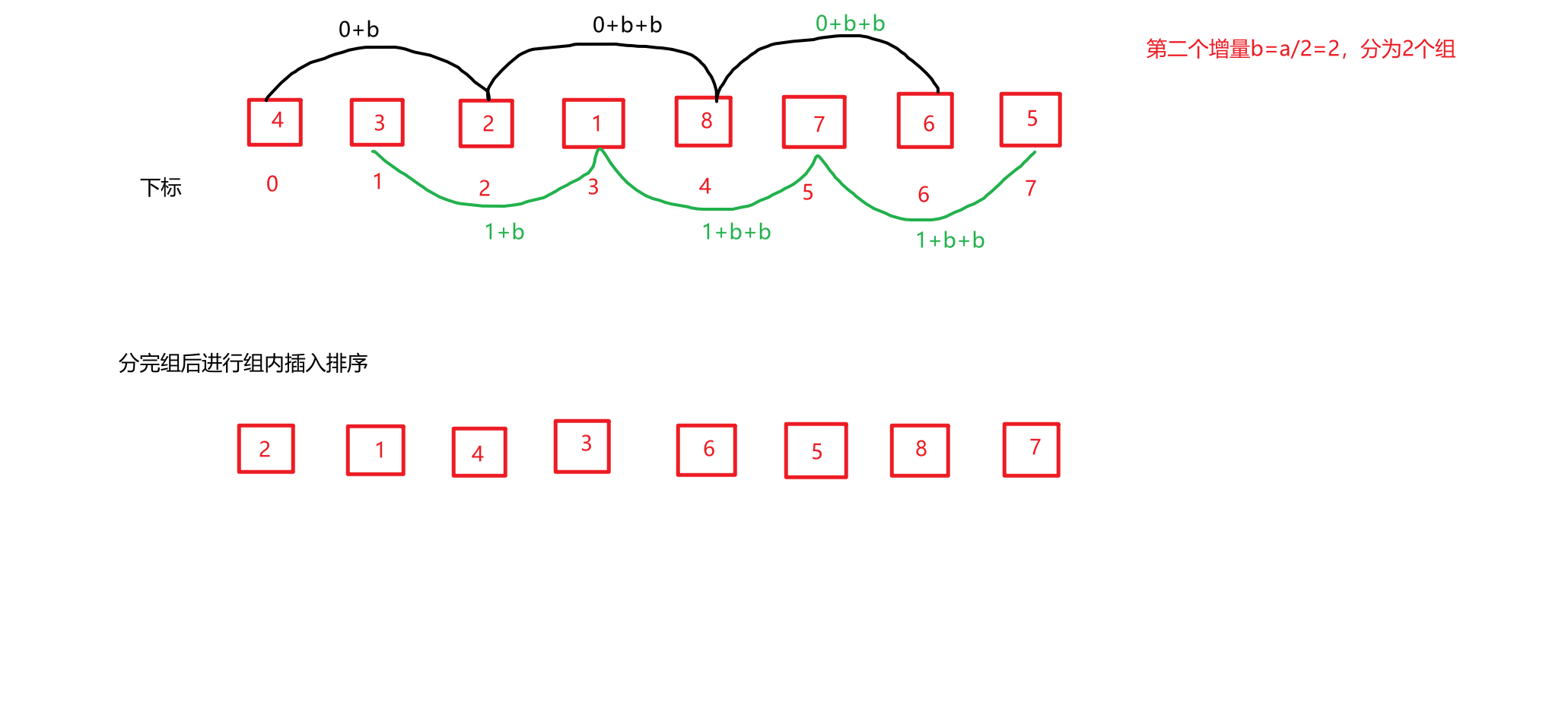
a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def hill_sort(a, n):
    # 先取增量为数组长度
    gap = n
    
    # 循环结束的条件，gap=1就是最后一次分组，此时gap/2=0，循环就结束了
    while gap > 0:
        # 每次gap取半
        gap = int(gap / 2)
        # 增量是多少就有几个组，所以我们需要对每个组进行插入排序
        for i in range(0, gap):
            # 对其中一组进行插入排序
            for j in range(i, n, gap):
                end = j
                # 这里需要判断下标是否超出了原数组的长度，其它的操作都是和插入排序一样的
                if end + gap >= n:
                    break
                wait = a[end + gap]
                while end >= 0:
                    if wait < a[end]:
                        a[end + gap] = a[end]
                        end -= gap
                    else:
                        break
                a[end + gap] = wait

    return a

print(hill_sort(a, len(a)))

下面的代码少了一个循环，就是单独都每个组进行插入排序的那个循环。

a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def hill_sort(a, n):
    gap = n
    while gap > 0:
        gap = int(gap / 2)
        for i in range(0, n):
            end = i
            if end + gap >= n:
                continue
            wait = a[end + gap]
            while end >= 0:
                if wait < a[end]:
                    a[end + gap] = a[end]
                    end -= gap
                else:
                    break
            a[end + gap] = wait

    return a

print(hill_sort(a, len(a)))

5. 归并排序

归并排序采用分治策略，分即将一个序列拆分成许多小序列进行排序，治就是将排好序的小序列合起来再进行排序。

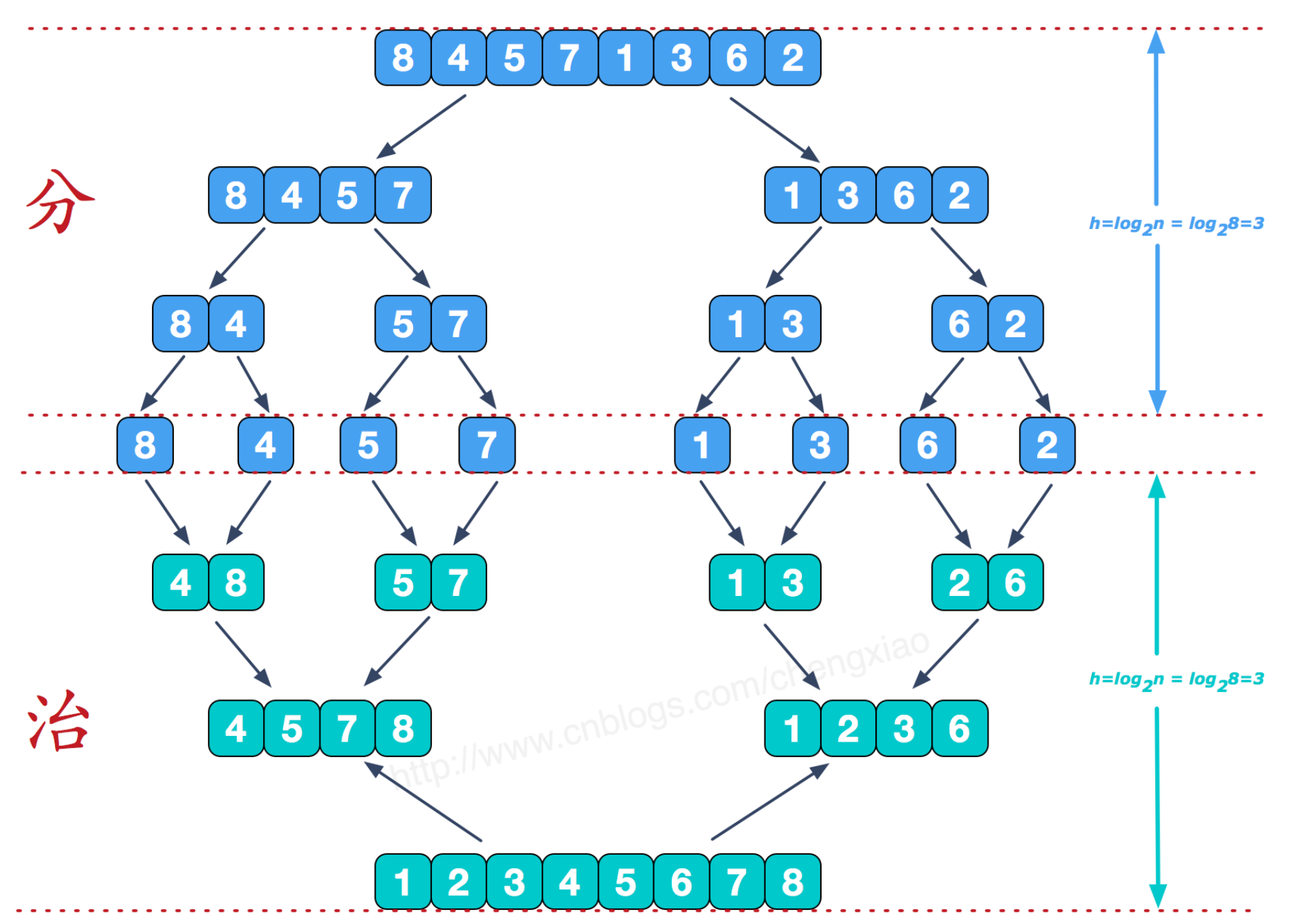
有两种实现方式：递归和迭代

• 递归：实现递归的时候不要多想，假设递归一次就成功。

a = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def merge_sort(a):
    # 数组长度
    n = len(a)
    
    # 递归终止条件。当数组不断被拆分，直至只剩一个元素时，递归就终止，开始一层一层地从里往外计算。
    if n <= 1:
        return a
    
    # 向下取整，如果数组是奇数大小，那么左边部分一定比右边部分小1
    mid = int(n / 2)
    
    # 拆分后将左边和右边部分分别进行递归
    # 其实就只有这里需要递归，所以这里写好后就不要去考虑一层一层嵌套的问题了
    left = merge_sort(a[:mid])
    right = merge_sort(a[mid:])
    
    # 用来存放“治”后的数组，也就是将两个数组中的元素按从小到大的顺序依次放入sort中
    sort = []
    
    i, j = len(left), len(right)
    
    # 这里是假设两个数组都有元素的情况，若其中一个数组元素被弹完了，循环终止
    while i and j:
        if left[0] <= right[0]:
            # 将小的一个添加到sort数组中
            sort.append(left[0])
            # 并将这个元素从原数组中弹出
            left.pop(0)
            i -= 1
        else:
            sort.append(right[0])
            right.pop(0)
            j -= 1
    
    # 当上面循环结束后只有两种情况：
    # 1. 两个数组元素都弹完
    # 2. 一个数组弹完，剩下一个数组未弹完
    # 那么我就需要将未弹完元素的数组弹尽，同时挨个添加到sort数组中
    while i:
        sort.append(left[0])
        left.pop(0)
        i -= 1
    while j:
        sort.append(right[0])
        right.pop(0)
        j -= 1
    return sort

print(merge_sort(a))

• 迭代（不会，2024.1.7）

6. 快速排序

快速排序跟冒泡排序很像，都是通过交换两元素位置来排序的。

快速排序需要一个基准元素（通常取数组的第一个元素）和left、right两个左右指针。它就是通过不断将元素与基准元素比较，比基准元素小就放在它的左边，比基准元素大就放在它的右边，然后再让基准元素左边那一段和右边那一段分别进行递归。

left指针一定指向的是数组的左边界（不一定是0）

right指针一定指向的是数组的有边界（不一定是数组的长度-1）

步骤：

• 判断递归结束的条件
• 用i和j来代替left和right，边界是固定的，是为了继续向下递归
• 定义基准元素
• 开始执行循环比较：
• • 若右指针指向的元素>=基准元素：右指针左移
  • 若右指针指向的元素<=基准元素：右指针指向的元素和左指针指向的元素交换
• • 若左指针指向的元素<=基准元素：左指针右移
  • 若左指针指向的元素>=基准元素：左指针指向的元素和右指针指向的元素交换

arr = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def quick_sort(arr, left, right):

    # 递归结束条件
    if left >= right:
        return

    # 用i和j分别作为左、右指针来进行移动过
    # 不能直接用left和right来当作指针，它们是用来当作边界的
    # left用来规定一段递归的起点，right用来规定另一段递归的终点
    i = left
    j = right
    # 基准数
    base = arr[i]

    # 当左指针始终小于右指针的时候，不断地移动指针和交换指针所指向的元素
    while i < j:

        # 如果右指针指向的元素>基准数，右指针左移
        while i < j and arr[j] >= base:
            j -= 1
        # 当上面循环结束时，表示右指针指向的元素小于基准数，将右指针指向的元素与左指针指向的元素交换（只是元素交换位置）
        arr[j], arr[i] = arr[i], arr[j]

        # 如果左指针指向的元素<基准数，左指针右移
        while i < j and arr[i] <= base:
            i += 1
        # 当上面循环结束时，表示左指针指向的元素大于基准数，将左指针指向的元素与右指针指向的元素交换
        arr[i], arr[j] = arr[j], arr[i]

    # 当上面循环结束后，左指针和右指针一定是相等的
    quick_sort(arr, left, i - 1)
    quick_sort(arr, i + 1, right)

quick_sort(arr, 0, len(arr) - 1)
print(arr)

7. 堆排序

堆排序本质上还是对数组排序，只是将数组中的元素按树结构的方式排序。

堆本质上也是一棵二叉树。分为大顶堆和小顶堆。大顶堆就是每个根节点的值一定大于等于其左右子节点的值，小顶堆类同。

如何将数组排列成一个堆？

• 将数组元素依次从上到下，从左到右排列

堆排序一共分为两大步：

• 将数组排列成一个大顶堆，其中每个根节点都应该满足大顶堆的要求
• 将堆顶元素与堆中最后一个元素交换，然后将最后一个元素排除在堆外，再重新对这个堆进行大顶堆化。直到排除掉最后一个元素为止

避坑：

• 最后一个非叶子节点一定是处于length / 2 - 1的位置，它前面的节点也一定有子节点

代码参考：
https://www.hello-algo.com/chapter_sorting/heap_sort/#1171
https://zq99299.github.io/dsalg-tutorial/dsalg-java-hsp/11/01.html#%E5%AE%8C%E6%95%B4%E5%AE%9E%E7%8E%B0

arr = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

# 调整堆结构（保持大顶堆）
def adjust_heap(arr, pos, length):
    """

    Args:
        arr: 要调整的堆（数组）
        pos: 调整的起始位置（非叶子节点）
             如果是创建大顶堆，则pos表示的是最下层最右边的那个非叶子节点
        length: 堆的长度
                    - 如果是创建堆，则length不变
                    - 如果是将根节点元素与堆尾元素交换，则每执行一次length-1
    Returns:

    """
    while True:
        # 左子节点的位置
        l = pos * 2 + 1

        # 右子节点的位置
        r = pos * 2 + 2

        # max表示值最大的节点的位置，在调整之前，假定是根节点的位置
        max = pos

        # 如果左子节点的位置（下标）在堆长度范围内且左子节点元素的值大于它的父节点的值
        if l < length and arr[l] > arr[max]:
            # max表示的就是左子节点的位置（值更大元素的位置）
            max = l
        # 如果右子节点的位置在堆长度范围内且右子节点元素的值大于它的父节点的值
        if r < length and arr[r] > arr[max]:
            # max表示的就是右子节点的位置
            max = r

        # 如果左右子节点都不大于根节点，max就表示的是根节点的位置，而pos始终都表示根节点的位置，此时就退出循环
        if max == pos:
            break

        # 如果左右子节点有一个大于根节点，则交换两个元素
        arr[pos], arr[max] = arr[max], arr[pos]

        # 然后又将交换的那个子节点作为根节点，对它下面的堆继续调整
        # 因为如果该子节点也是一个堆，它是堆中最大的元素
        # 但当它的父节点比它小，从而它和父节点交换，此时它的值在它的堆中就不一定是最大的
        # 另一个子节点自然不用考虑，它肯定是它堆中最大的
        pos = max



def heap_sort(arr):
    # 将数组创建为一个大顶堆
    for i in range(int(len(arr) / 2) - 1, -1, -1):
        adjust_heap(arr, i, len(arr))

    # 交换堆顶元素与堆最后一个元素，然后将最后一个元素排除堆
    # 将交换后的堆又调整成为一个大顶堆
    for i in range(len(arr) - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        adjust_heap(arr, 0, i)

heap_sort(arr)
print(arr)

8. 计数排序

计数排序顾名思义就是通过计算arr数组中元素的出现次数来进行排序。

需要额外一个数组来计算arr数组中元素的出现次数。

计数数组的长度为arr数组中最大值（max）-最小值（min）+1。

计数数组的下标区间：[0, max-min+1)，当下标区间都加上一个min后：[min, max+1)

右边是开区间是因为数组长度为max-min+1，而数组的下标是从0开始的。

arr = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def counting_sort(arr):
    # 先获取数组中的最大值和最小值
    min = arr[0]
    max = arr[0]
    for i in range(1, len(arr)):
        if arr[i] <= min:
            min = arr[i]
        if arr[i] >= max:
            max = arr[i]

    # 计数用的数组，数组的大小为arr中最大值-最小值+1，该数组的下标就用来表示min到max之间的数
    counter = [0] * (max - min + 1)

    # 统计arr数组中每个元素出现的次数
    for i in range(len(arr)):
        # counter的下标相当于在一个区间[0, max-min+1]，当它的下标加上一个min就表示[min,max]之间的所有数
        # max-min“+1”是因为下标是从0开始的
        counter[arr[i] - min] += 1

    # n用来表示arr中元素的下标
    n = 0
    for j in range(len(counter)):
        # counter数组中的值，就表示它的下标加上min的值这个数出现的次数
        while counter[j] != 0:
            arr[n] = j + min
            counter[j] -= 1
            n += 1

counting_sort(arr)
print(arr)

9. 桶排序

桶排序就是先确定几个桶，然后将数组中的元素按照某种规则放入桶中，分别对每个桶中的元素进行排序，然后再依次从第一个桶开始将元素拿出来。（后一个桶中的元素的值一定大于前一个桶中元素的值）。

• 一个桶放几个元素（bucketSize）：人为规定或使用默认值
• 桶数量的确定（bukcetNum）：arr数组中的（max - min + 1）/ bucketSize
• 确定元素放入哪个桶：bucket[(arr[i] - min) / bucketSize]

arr = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def bucket_sort(arr, bucketSize=5):
    """

    Args:
        arr:
        bucketSize: 每个桶的容量

    Returns:

    """

    # 找出arr数组中最大值和最小值
    max = arr[0]
    min = arr[0]
    for i in range(len(arr)):
        if max < arr[i]:
            max = arr[i]
        if min > arr[i]:
            min = arr[i]

    # 区间【min，max】一共有max-min+1个数，一个桶装bucketSize个数，所以相除就得到了桶的数量
    # 最后再加个1是防止前面被除数小于除数，结果就为0个桶，显然是不行的
    bucketNum = int((max - min + 1) / bucketSize + 1)

    # 初始化桶
    bucket = []
    for j in range(bucketNum):
        bucket.append([])

    # 将arr数组中的元素按照范围放入桶中
    # 可以看到前面桶的数量的定义，要确定放入哪个桶，(arr[i]-min)/bucketSize就能确定桶号
    for k in range(len(arr)):
        bucket[int((arr[k] - min) / bucketSize)].append(arr[k])
    
    # 桶内进行排序，各种排序方式都行
    for i in range(len(bucket)):
        # 这里使用的是前面的快速排序
        quick_sort(bucket[i], 0, len(bucket[i]) - 1)
    
    # 将桶内元素排完序后，从第一个桶开始，依次将桶内元素替换掉arr数组中的元素
    n = 0
    for i in range(len(bucket)):
        if bucket[i]:
            for j in range(len(bucket[i])):
                arr[n] = bucket[i][j]
                n += 1


bucket_sort(arr)
print(arr)

10. 基数排序

基数排序是桶排序的拓展，假如排序的数是十进制的，那么每一个数的每一位有10种表示，那么就创建10个桶。

从个位开始，每个数的个位是多少，就放入哪个桶。全部放完后再从第一个桶开始取出来挨个放入原数组，先放进去的先取。

然后从十位开始…

当排序到最后一轮的时候，再取出来放入原数组，这时原数组就有序了。

arr = [21,3,10,33,9,22,34,18,26,15,100,2,11,31,52]

def radix_sort(arr):
    # 找出arr数组中最大的元素
    max = arr[0]
    for i in range(len(arr)):
        if max < arr[i]:
            max = arr[i]

    # 得到它的位数
    sortNum = len(str(max))


    # 因为是十进制的排序，所以十个桶就行了
    bucketNum = 10

    # 初始化桶
    bucket = []
    for i in range(bucketNum):
        bucket.append([])

    # n是用来辅助求得个位上的数，例如123 / n % 10 = 3      int(123 / (n * 10)) % 10 = 2....
    n = 1

    # 最大元素有几位就要进行几次排序
    for i in range(sortNum):

        # 初始化桶的计数数组，记录每个桶有多少个元素
        counter = [0 for j in range(bucketNum)]

        # 将元素按照它们个位个位、十位等等的数分别放入桶中
        for k in range(len(arr)):
            # 得到个位或十位等等上的数
            d = int(arr[k] / n) % 10
            # 放入相应的桶中
            bucket[d].append(arr[k])
            # 放入一个就加1
            counter[d] += 1

        # 指示arr数组元素的位置
        index = 0
        # 开始依次将每个桶中的元素取出，从第一个桶开始，先放进去的先出来
        for m in range(len(counter)):
            while counter[m] != 0:
                arr[index] = bucket[m].pop(0)
                index += 1
                counter[m] -= 1
        # 这里一定要记得
        n *= 10
radix_sort(arr)
print(arr)