【算法】使用位运算解算法题(C++)
发布时间:2023年12月28日
文章目录
0. 位运算 基本介绍
我们知道,一般基本位运算分为以下几种:
- & 按位与:有0则为0
- | 按位或:有1则为1
- ^ 按位异或:记法有2
- 相同为0,相异为1
- 不进位相加(00->0, 01->1, 11->0,相当于两数相加但不进位)
- ~ 按位取反:对操作数按位取反,即0变为1,1变为0。
- << 向左移动:相当于将其乘以2的若干次方
- >> 向右移动:相当于将其除以2的若干次方
1. 位运算基本使用 + 连带题目
当我们理解了基础位运算,我们要确保可以解决下图红字中的基本问题:
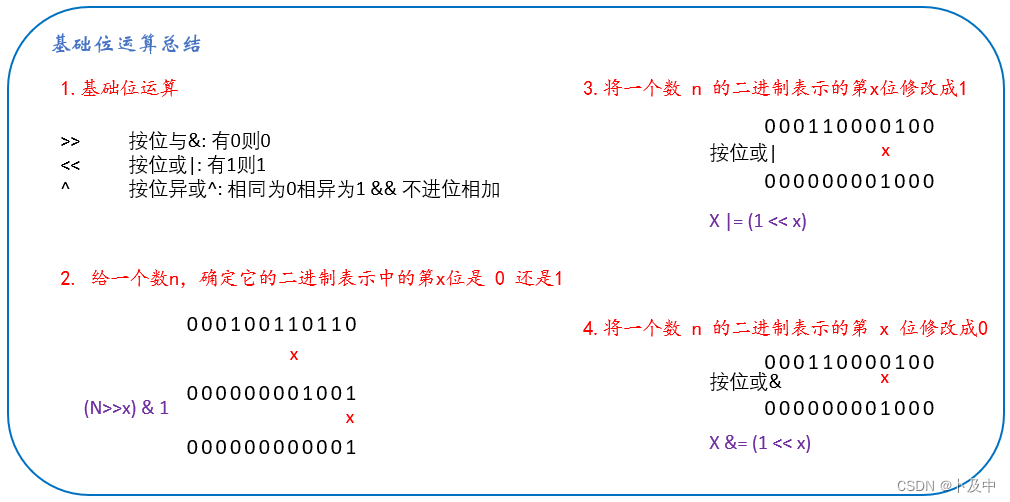

通过上图设计的题目和思路,我们可以顺势解决以下几道题:
191.位1的个数

思路:

如图,我们只需要 将n的每一位都&1 即可:
- 将n&1,结果更新到ret
- n右移一位,持续此过程直到n为0
代码:
int hammingWeight(uint32_t n) {
int ret = 0; // 记录结果
while (n)
{
ret += n & 1;
n >>= 1;
}
return ret;
}
338.比特位计数

思路:
题目要求计算一个(1~n)范围内每个元素,二进制中1的个数 :
- 创建结果数组ret,变量count记录当前元素二进制中1的个数
- 将整个过程放到一个从0~n的循环中
- 计算当前元素位一的个数
- 将count给到ret,直至循环结束,返回ret
代码:
vector<int> countBits(int n) {
vector<int> ret(n+1, 0);
for(int i = 0; i <= n; ++i) // 统计0 ~ n中每个元素二进制位一的个数
{
int count = 0;
int tmp = i;
while(tmp) // 计算tmp中1的个数
{
count += tmp & 1;
tmp >>= 1;
}
// 存储其1的个数
ret[i] = count;
}
return ret;
}
461.汉明距离

思路:

如图所示,我们知道异或相当于(相同为0,相异为1),只需要统计两数异或之后的结果中1的个数即就是不同位的个数,即汉明距离。
代码:
int hammingDistance(int x, int y) {
int ret = 0;
int tmp = x ^ y;
// 异或后 1的个数 即为 二进制位不同位置数
while(tmp)
{
ret += tmp & 1;
tmp >>= 1;
}
return ret;
}
136.只出现一次的数字

思路:
题目要求找到整数数组中只出现过一次的数字,此题可以用哈希表解题,但位运算的时间空间复杂度总体更为优秀。
- 我们知道,a ^ a = 0; b ^ 0 = b;
- 根据该思路,将数组所有元素异或,剩余元素即为只出现一次的。
代码:
int singleNumber(vector<int>& nums) {
int ret = 0;
// 将全部元素异或,结果为只出现一次的数字
for(int i : nums){
ret ^= i;
}
return ret;
}
260.只出现一次的数字III

思路:
- 首先异或所有元素,得到tmp(所求两数的异或结果)
- 将tmp & -tmp 得到两元素的不同位differ
- 根据此不同位进行划分:
- 如果当前元素num与differ按位与的结果不等于0,则a ^= num
- 反之, b ^= num
- 最后a,b即为两个只出现一次的数字。
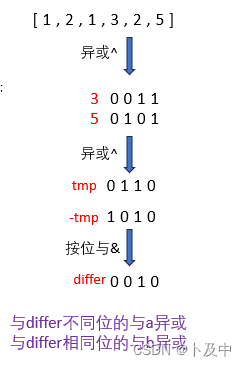
代码:
vector<int> singleNumber(vector<int>& nums) {
int tmp = 0;
for(int num : nums) tmp ^= num; // 全部元素异或
// 防止溢出
int differ = (tmp == INT_MIN ? tmp : tmp & (-tmp)); // 找a,b的不同位
int a = 0, b = 0;
for(int num : nums)
{ // 根据条件划分
if((num & differ) != 0)
a ^= num;
else
b ^= num;
}
return {a, b};
}
2. 使用位运算解决算法题
上面的题是小试牛刀,下面的题正式进行位运算算法的代码编写。
面试题01.01.判定字符是否唯一

思路:
上题解法利用位图思想 :我们通过将字符串的每个元素存到int型变量bitMap中(该位为0:未出现过,为1:出现过),通过判断所有位是否有1则可判断字符串的字符是否唯一。
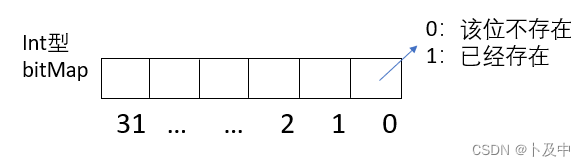
代码:
bool isUnique(string astr) {
// 位图
if(astr.size() > 26) return false;
int bitMap = 0; // 从后向前存放字母的出现次数,0代表未出现过,1代表出现过
for(char ch : astr)
{
int i = ch - 'a'; // 取该字符位
if((bitMap >> i) & 1 == 1) return false; // 如果这一位存在,false
bitMap |= (1 << i);
}
return true;
}
371.两整数之和

题意很清晰:即不使用±运算符计算两个整数的和。
思路:
我们知道:
- 按位异或^ = 不进位相加,而我们需要相加的结果,则只需要找到进位即可。
- 而(a & b)就是进位结果,但我们进位是向前一位进位,所以进位为(a & b) << 1。重复上述步骤,直到进位为0,就得到了最终结果。
代码:
int getSum(int a, int b) {
while(b != 0)
{
int nsum = a ^ b; // 不进位相加结果
int carry = (a & b) << 1; // 进位数
a = nsum;
b = carry; // 重复步骤直到b==0
}
return a;
}
137.只出现一次的数字II

思路:
-
定义一个
vector<int> count(32),用于存储nums中所有元素的二进制表示的各个位的出现次数; -
对于记录完毕的count,count的每一位都有如下四种情况:
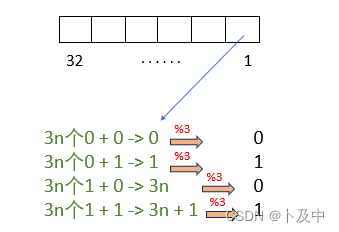
- 如图所示,即0, 1, 3n, 3n + 1四种情况
- 而对这四种情况模3后结果有两种情况:0 和 1
-
将得出的结果还原到ret中(用|=还原)
代码:
int singleNumber(vector<int>& nums) {
vector<int> count(32); // 存放数组所有元素的位
for(int num : nums)
for(int i = 0; i < 32; ++i) // 存
{
count[i] += (num >> i) & 1;
}
// 遍历count中的32个元素,还原只出现一次的元素到ret中
int ret = 0;
for(int i = 0; i < 32; ++i)
{
ret |= (count[i] % 3) << i;
}
return ret;
}
面试题17.04.消失的数字

思路:
我们知道:a ^ a = 0 且 0 ^ b = b ,则利用这个性质,将nums中的数与0~n的所有数异或,最终结果则为消失的数字。
代码:
int missingNumber(vector<int>& nums) {
// 位运算
int n = nums.size();
int miss = 0;
for(int i = 0; i < n; ++i) // 与数组所有元素and 0~n-1的元素异或
{
miss ^= i ^ nums[i];
}
miss ^= n; // 异或n
return miss;
}
面试题17.19.消失的两个数字
思路:
“只出现一次的数字Ⅲ” 中有个思想就是通过两元素的不同位,进行划分,这里也是一样
- 异或所有数:得到缺失的两个数字的异或和
- 获取 tmp 中最右边为 1 的位数:找到两个缺失数字的不同位
- 根据 differ 的值,将数组元素划分为两组进行异或操作
代码:
vector<int> missingTwo(vector<int>& nums) {
int tmp = 0;
int n = nums.size() + 2; // 数组中缺失两个数字,所以数组长度为n+2
// 1. 异或所有数
for (int i = 1; i <= n; ++i)
tmp ^= i;
for (int num : nums)
tmp ^= num;
// 2. 获取最右边为1的位数(不同位)
int differ = tmp & -tmp;
// 3. 根据differ,划分数组元素进行异或
int a = 0, b = 0;
for (int i = 1; i <= n; ++i) {
if (i & differ)
a ^= i;
else
b ^= i;
}
for (int num : nums) {
if (num & differ)
a ^= num;
else
b ^= num;
}
return {a, b};
}
文章来源:https://blog.csdn.net/Dreaming_TI/article/details/134705058
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 解决vld内存泄露检测工具只支持到vs2015的问题,visual studio2015以上版本安装vld内存泄漏检测工具[实测vs2022生效]
- Java重写ArrayList方法
- SSH
- springboot 东方通(tongweb)替换tomcat(国产化)
- 如何设置gitlab.rb 将所有数据运行目录放置到指定目录
- 解决CDN的网站后台无法获取访客真实ip的问题
- juejin小册git的使用2上手 1:新公司用 Git 管理代码,怎么快速上手?
- Netty和Reactor设计模式
- JavaWeb笔记之SVN
- 2024肥晨赠书活动第一期:《实战AI大模型》