线索二叉树（C语言实现）

发布时间：2024年01月03日

前面几节给大家依次介绍了二叉树的先序、中序、后序遍历，无论采用哪种遍历方式，最终可以得到一个由二叉树所有结点构成的线性序列。

以下图这棵二叉树为例：

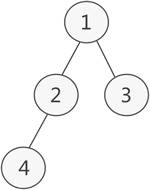
图 1 二叉树

先序、中序和后序遍历二叉树，最终得到的线性序列分别是：

  • 先序序列：1 2 4 3
  • 中序序列：4 2 1 3
  • 后序序列：4 2 3 1

你可以这样理解，遍历二叉树的过程就是将非线性的树型结构转换为线性结构。在线性序列中，每个结点（除最后一个结点）都有自己的直接后继结点，每个结点（除第一个结点）也有自己的直接前驱结点。

整个遍历二叉树的过程，实则在不断地寻找各个结点的直接后继结点。当然在某些场景中，还可能需要寻找某个结点的直接前驱结点。在二叉树中，我们可以很容易地找到某个结点的孩子结点，但找到某个结点的前驱和后继结点是比较困难的，目前掌握的方法就只能遍历整棵二叉树。

本节给大家介绍一种更高级的存储方案，可以提高在二叉树中查找前驱和后继结点的效率，也可以提高遍历二叉树的效率，称为线索二叉树。

什么是线索二叉树

使用链表存储二叉树时，对于由 n 个结点组成的二叉树，整个存储结构中一定包含 n+1 个空指针。

下图给大家展示了图 1 中的二叉树在链表中的存储状态&

文章来源:https://blog.csdn.net/qq_25775935/article/details/135326888
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章