实验七 基于广度优先搜索的六度空间 理论验证

实验七 基于广度优先搜索的六度空间理论验证

一．实验目的
1.掌握图的邻接矩阵和邻接表表示法，掌握采用邻接矩阵和邻接表表示法创
建图的算法。
2.掌握图的广度优先搜索算法。
3.掌握基于图的广度优先搜索的六度空间理论验证的算法。

二、实验内容
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论
可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个，也就是
说，最多通过五个人你就能够认识任何一个陌生人。”假如给你一个社交网络图，
请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。

三、实验实习设备及开发环境
Visual studio 2022
四．实验实习过程步骤（注意是主要关键步骤，不是所有步骤，适当文字+截图说明）
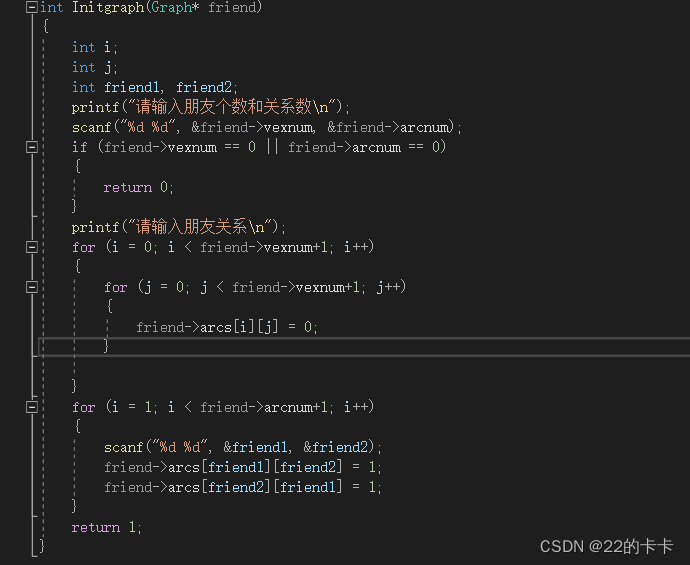
Function1：初始化图，与上一个实验不一样的是，这里边的权重用1和0表示，（1表示有关系，0表示没关系），然后因为是无向图，所以对称的关系都需要赋值。

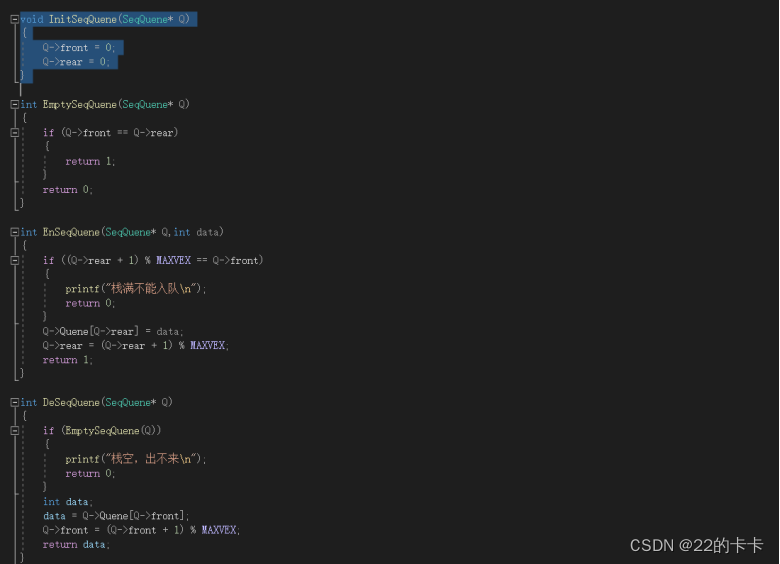
Function2：栈的基本操作，因为需要BFS算法需要用到栈的基本操作。这里有，初始化，入栈，出栈，判断栈是否为空。

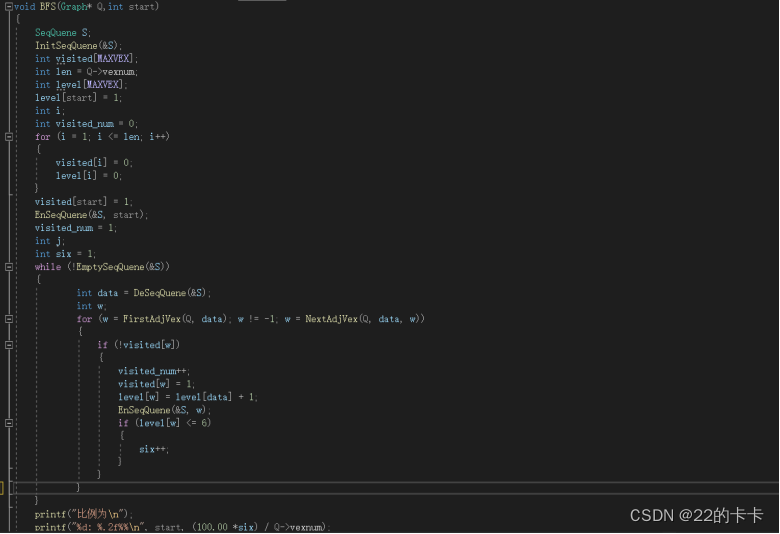
Function3：BFS算法。从start进入，将他标记为已访问，并且入栈，栈里面是需要顺序访问的元素，level数组用于记录步数。从栈里面的元素开始访问，访问与元素相邻的一些节点，如果这些节点没有被访问过，就入栈，并且标记为访问的，并且他们距离start的距离，也是在原来的节点距离上加1，如果他们的距离是小于6的，就记一次数。一直访问到所有节点都被访问完，栈空的时候。

五．实验实习结果及分析

实验结果成功。

六．实验遇到的问题及解决办法，实验心得体会及对此实验的意见或建议（有就写，无可不写）。
源码：

#include <stdio.h>
#include <stdlib.h>
#define MAX 999999
#define MAXVEX 100

typedef struct graph
{
	int Vexs[MAXVEX];
	int arcs[MAXVEX][MAXVEX];
	int vexnum, arcnum;
}Graph;
typedef struct SeqQuene
{
	int Quene[MAXVEX];
	int front;
	int rear;

}SeqQuene;

void InitSeqQuene(SeqQuene* Q)
{
	Q->front = 0;
	Q->rear = 0;
}

int EmptySeqQuene(SeqQuene* Q)
{
	if (Q->front == Q->rear)
	{
		return 1;
	}
	return 0;
}

int EnSeqQuene(SeqQuene* Q,int data)
{
	if ((Q->rear + 1) % MAXVEX == Q->front)
	{
		printf("栈满不能入队\n");
		return 0;
	}
	Q->Quene[Q->rear] = data;
	Q->rear = (Q->rear + 1) % MAXVEX;
	return 1;
}

int DeSeqQuene(SeqQuene* Q)
{
	if (EmptySeqQuene(Q))
	{
		printf("栈空，出不来\n");
		return 0;
	}
	int data;
	data = Q->Quene[Q->front];
	Q->front = (Q->front + 1) % MAXVEX;
	return data;
}
int Initgraph(Graph* friend)
{
	int i;
	int j;
	int friend1, friend2;
	printf("请输入朋友个数和关系数\n");
	scanf("%d %d", &friend->vexnum, &friend->arcnum);
	if (friend->vexnum == 0 || friend->arcnum == 0)
	{
		return 0;
	}
	printf("请输入朋友关系\n");
	for (i = 0; i < friend->vexnum+1; i++)
	{
		for (j = 0; j < friend->vexnum+1; j++)
		{
			friend->arcs[i][j] = 0;
		}

	}
	for (i = 1; i < friend->arcnum+1; i++)
	{
		scanf("%d %d", &friend1, &friend2);
		friend->arcs[friend1][friend2] = 1;
		friend->arcs[friend2][friend1] = 1;
	}
	return 1;
}

int FirstAdjVex(Graph* friend, int p)
{
	int j;
	for (j = 1; j <= friend->vexnum; j++)
	{
		if (friend->arcs[p][j] == 1)
		{
			return j;
		}
	}
	return -1;
}

int NextAdjVex(Graph* friend, int p, int w)
{
	int i, j;
	for (j = w + 1; j <= friend->vexnum; j++)
	{
		if (friend->arcs[p][j] == 1)
		{
			return j;
		}
	}
	return -1;
}
void BFS(Graph* Q,int start)
{
	SeqQuene S;
	InitSeqQuene(&S);
	int visited[MAXVEX];
	int len = Q->vexnum;
	int level[MAXVEX];
	level[start] = 1;
	int i;
	int visited_num = 0;
	for (i = 1; i <= len; i++)
	{
		visited[i] = 0;
		level[i] = 0;
	}
	visited[start] = 1;
	EnSeqQuene(&S, start);
	visited_num = 1;
	int j;
	int six = 1;
	while (!EmptySeqQuene(&S))
	{
			int data = DeSeqQuene(&S);
			int w;
			for (w = FirstAdjVex(Q, data); w != -1; w = NextAdjVex(Q, data, w))
			{
				if (!visited[w])
				{
					visited_num++;
					visited[w] = 1;
					level[w] = level[data] + 1;
					EnSeqQuene(&S, w);
					if (level[w] <= 6)
					{
						six++;
					}
				}
			}
	}
	printf("%d: %.2f%%\n", start, (100.00 *six) / Q->vexnum);
}
int main()
{
	Graph friend;
	int i;
	while (Initgraph(&friend))
	{
		for (i = 1; i <= friend.vexnum; i++)
		{
			printf("比例为\n");
			BFS(&friend, i);
		}
		
	}
	return 0;
}