力扣198. 打家劫舍(java 动态规划)
Problem: 198. 打家劫舍
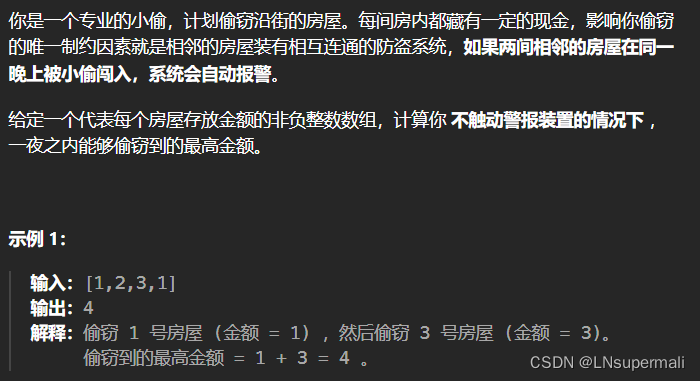
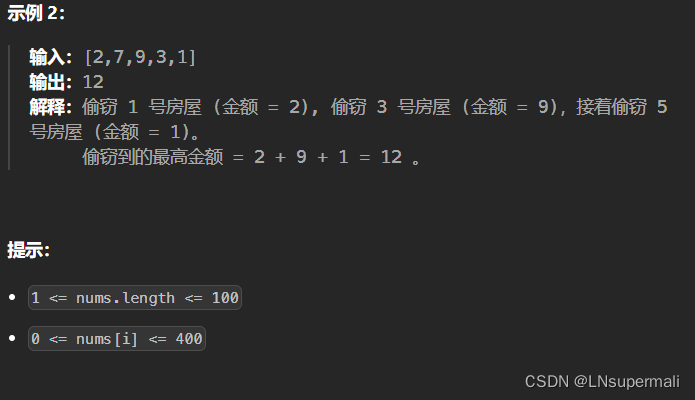
题目描述
思路
1.构建多阶段决策模型:n个房屋对应n个阶段,每一个阶段决定一个房间是偷还是不偷,两种决策:偷、不偷
2.定义状态:不能记录每个阶段决策完之后,小偷可偷的最大金额,需要记录不同决策对应的最大金额,也就是:这个房屋偷-对应的最大金额;这个房屋不偷-对应的最大金额。int[n][2]记录每个阶段的状态,dp[i][0]表示第i个物品不偷,当下剩余的最大金额;dp[i][1]表示第i个物品偷,当下剩余的最大金额;
3.定义状态转移方程:dp[i][0] = max(dp[i - 1][0], dp[i - 1][1])即表示假设不偷则当前阶段可以获得的最大值为上一个房屋偷或者不偷的二者中的最大金额;dp[i][1] = dp[i - 1][0] + nums[i]即表示假设当前阶段偷则当前可以获得的最大金额为上一个房屋不偷加上当前当前房屋的金额
解题方法
1.获取nums数组的长度为n;并定义int类型数组dp:int[][] dp = new int[n][2];
2.初始化dp[0][0]为0,dp[0][1]为nums[0];
3.完成动态转移方程;
4.返回max(dp[n - 1][0], dp[n - 1][1])
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为数组nums的长度
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {
/**
* Get the maximum amount
*
* @param nums Given array(Store the amount of each house)
* @return int
*/
public int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
int n = nums.length;
int[][] dp = new int[n][2];
//dp[i][0] represents the maximum amount
// that can currently be obtained without stealing
dp[0][0] = 0;
//dp[i][1] represents the maximum amount
// that can be obtained when not stealing
dp[0][1] = nums[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = dp[i - 1][0] + nums[i];
}
return Math.max(dp[n - 1][0], dp[n - 1][1]);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 插件化简单介绍
- 大厂HR大揭秘!年底才是找工作的黄金期
- selenium利用图鉴 破点击验证码 登录b站
- 烦恼的高考志愿(洛谷)已过加强测试点
- html中的form表单以及相关控件input、文本域、下拉select等等的详细解释 ,点赞加关注持续更新~
- 页面跳转后,默认选中tree节点并高亮显示
- 【NSX-T】10. 搭建NSX-T环境 —— 使用 BGP 配置 Tier-0 网关
- Spring高手之路-Spring支持的注入方式、Spring为什么不建议使用基于字段的依赖注入
- QT-CAD-3D显示操作工具
- 动态规划问题