MATLAB中var函数用法
目录
????????var函数的功能是求取方差。
语法
V = var(A)
V = var(A,w)
V = var(A,w,"all")
V = var(A,w,dim)
V = var(A,w,vecdim)
V = var(___,nanflag)
[V,M] = var(___)说明
????????V = var(A) 返回 A 沿大小大于 1 的第一个数组维度计算的元素的方差。默认情况下,方差按 N-1 实现归一化,其中 N 是观测值数量。
-
如果 A 是观测值的向量,则 V 是标量。
-
如果 A 是一个列为随机变量且行为观测值的矩阵,则 V 是一个包含与每列对应的方差的行向量。
-
如果 A 是多维数组,则 var(A) 沿大小大于 1 的第一个数组维度计算,并将这些元素视为向量。此维度中 V 的大小变为 1,而所有其他维度的大小仍与在 A 中相同。
-
如果 A 是标量,则 V 为 0。
-
如果 A 是一个 0×0 的空数组,则 V 为 NaN。
-
如果 A 是表或时间表,则 var(A) 返回单行表,其中包含每个变量的方差。 (自 R2023a 起)
V = var(A,w) 指定加权方案。当 w = 0(默认值)时,方差按 N-1 实现归一化,其中 N 是观测值数量。如果 w = 1,则方差按观测值数量实现归一化。w 也可以是包含非负元素的权重向量。在这种情况下,w 的长度必须等于 var 将作用于的维度的长度。
????????当 w 为 0 或 1 时,V = var(A,w,"all") 返回 A 的所有元素的方差。
V = var(A,w,dim) 返回沿维度 dim 计算的方差。要维持默认归一化并指定运算的维度,请在第二个参数中设置 w = 0。
????????当 w 为 0 或 1 时,V = var(A,w,vecdim) 返回向量 vecdim 中指定维度的方差。例如,如果 A 是矩阵,则 var(A,0,[1 2]) 返回 A 中所有元素的方差,因为矩阵的每个元素包含在由维度 1 和 2 定义的数组切片中。
V = var(___,nanflag) 在上述任一语法的基础上指定包含还是省略 A 中的 NaN 值。例如,var(A,"omitnan") 在计算方差时会忽略 NaN 的值。默认情况下,var 包括 NaN 值。
[V,M] = var(___) 还返回 A 中用于计算方差的元素的均值。如果 V 是加权方差,则 M 是加权均值。
示例
矩阵方差
????????创建一个矩阵并计算其方差。
A = [4 -7 3; 1 4 -2; 10 7 9];
var(A)
ans = 1×3
21.0000 54.3333 30.3333数组方差
????????创建一个三维数组并计算其方差。
A(:,:,1) = [1 3; 8 4];
A(:,:,2) = [3 -4; 1 2];
var(A)
ans =
ans(:,:,1) =
24.5000 0.5000
ans(:,:,2) =
2 18指定方差权重向量
????????创建一个矩阵并根据权重向量?w?计算其方差。
A = [5 -4 6; 2 3 9; -1 1 2];
w = [0.5 0.25 0.25];
var(A,w)
ans = 1×3
6.1875 9.5000 6.1875指定方差的维度
????????创建一个矩阵并沿第一个维度计算其方差。
A = [4 -2 1; 9 5 7];
var(A,0,1)
ans = 1×3
12.5000 24.5000 18.0000沿第二个维度计算A的方差。
var(A,0,2)
ans = 2×1
9
4
数组页的方差
????????创建一个三维数组并计算每页数据(行和列)的方差。
A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
V = var(A,0,[1 2])
V =
V(:,:,1) =
6.2500
V(:,:,2) =
60
V(:,:,3) =
20.9167排除缺失值的方差
????????创建一个包含 NaN 值的矩阵。
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
A = 2×4
1.7700 -0.0050 NaN -2.9500
NaN 0.3400 NaN 0.1900
????????计算矩阵的方差,不包括 NaN 值。对于包含任一 NaN 值的矩阵列,var 使用非 NaN 元素进行计算。对于包含的值都是 NaN 的矩阵列,方差为 NaN。
V = var(A,"omitnan")
V = 1×4
0 0.0595 NaN 4.9298方差和均值
????????创建一个矩阵并计算每列的方差和均值。
A = [4 -7 3; 1 4 -2; 10 7 9];
[V,M] = var(A)
V = 1×3
21.0000 54.3333 30.3333
M = 1×3
5.0000 1.3333 3.3333????????创建一个矩阵,根据权重向量 w 计算每列的加权方差和加权均值。
A = [5 -4 6; 2 3 9; -1 1 2];
w = [0.5 0.25 0.25];
[V,M] = var(A,w)
V = 1×3
6.1875 9.5000 6.1875
M = 1×3
2.7500 -1.0000 5.7500参数说明
A — 输入数组
????????输入数组,指定为向量、矩阵、多维数组、表或时间表。如果 A 是标量,则 var(A) 返回 0。如果 A 是一个 0×0 的空数组,则 var(A) 返回 NaN。
w — 粗细
权重,指定为以下值之一:
-
0 - 按 N-1 实现归一化,其中 N 是观测值的数量。如果只有一个观测值,则权重为 1。
-
1 - 按 N 实现归一化。
-
由非负标量权重构成的向量,这些权重对应于沿其计算方差的 A 的维度。
dim — 沿其运算的维度
????????沿其运算的维度,指定为正整数标量。如果不指定维度,则默认为第一个大于 1 的数组维度。
????????维度?dim?表示长度减至?1?的维度。size(V,dim)?为?1,而所有其他维度的大小保持不变。
以一个?m×n?输入矩阵?A?为例:
-
var(A,0,1) 计算 A 的每列中元素的方差,并返回一个 1×n 行向量。
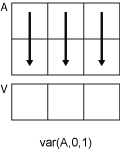
-
var(A,0,2) 计算 A 的每行中元素的方差,并返回一个 m×1 列向量。
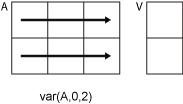
如果 dim 大于 ndims(A),则 var(A) 返回大小与 A 相同的由零组成的数组。
vecdim — 维度向量
????????维度向量,指定为正整数向量。每个元素代表输入数组的一个维度。指定的操作维度的输出长度为 1,而其他保持不变。
????????以 2×3×3 输入数组 A 为例。然后 var(A,0,[1 2]) 返回 1×1×3 数组,其元素是在 A 的每页上计算的方差。
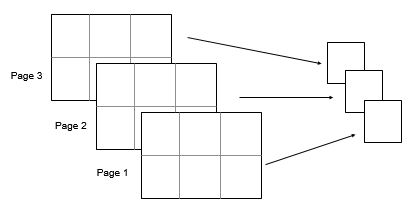
nanflag — 缺失值条件
缺失值条件,指定为下列值之一:
-
"includemissing" 或 "includenan" - 在计算方差时包括 A 中的 NaN 值。如果运算维度中的任一元素是 NaN,则 V 中的对应元素也是 NaN。"includemissing" 和 "includenan" 具有相同的行为。
-
"omitmissing" 或 "omitnan" - 忽略 A 和 w 中的 NaN 值,并基于较少的点计算方差。如果运算维度中的所有元素都是 NaN,则 V 中的对应元素是 NaN。"omitmissing" 和 "omitnan" 具有相同的行为。
V — 方差
方差,以标量、向量、矩阵、多维数组或表形式返回。
-
如果 A 是观测值的向量,则 V 是标量。
-
如果 A 是一个列为随机变量且行为观测值的矩阵,则 V 是一个包含与每列对应的方差的行向量。
-
如果 A 是多维数组,则 var(A) 沿大小大于 1 的第一个数组维度计算,并将这些元素视为向量。此维度中 V 的大小变为 1,而所有其他维度的大小仍与在 A 中相同。
-
如果 A 是标量,则 V 为 0。
-
如果 A 是一个 0×0 的空数组,则 V 为 NaN。
-
如果 A 是表或时间表,则 V 是单行表。如果 A 的变量有单位,则 V 的变量没有那些单位。 (自 R2023a 起)
M — 均值
均值,以标量、向量、矩阵、多维数组或表形式返回。
-
如果 A 是观测值的向量,则 M 是标量。
-
如果 A 是一个列为随机变量且行为观测值的矩阵,则 M 是一个包含与每列对应的均值的行向量。
-
如果 A 是多维数组,则 var(A) 沿大小大于 1 的第一个数组维度计算,并将这些元素视为向量。此维度中 M 的大小变为 1,而所有其他维度的大小仍与在 A 中相同。
-
如果 A 是标量,则 M 等于 A。
-
如果 A 是一个 0×0 的空数组,则 M 为 NaN。
-
如果 A 是表或时间表,则 M 是单行表。如果 A 的变量有单位,则 M 的变量有相同的单位。 (自 R2023a 起)
如果 V 是加权方差,则 M 是加权均值。
方差
????????对于由 N 个标量观测值组成的随机变量向量 A,方差定义为:
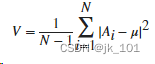
,其中 μ 是 A 的均值,
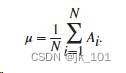
????????有些方差的定义使用归一化因子 N 而非 N – 1。可以通过指定权重?1?来使用归一化因子 N,从而生成样本关于其均值的二阶矩。
????????无论方差的归一化因子是什么,都假定均值具有归一化因子 N。
加权方差
????????对于由 N 个标量观测值组成的有限长度向量 A 和加权方案 w,加权方差被定义为

,其中 μw 是 A 的加权均值。
加权均值
????????对于由 N 个标量观测值组成的有限长度向量 A 和加权方案w,加权均值定义为
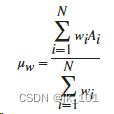
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 新版selenium4.0 + Python使用详解
- Linux网络编程(一-网络相关知识点)
- “超人练习法”系列07:熟练掌握的几个阶段
- 网站转小程序系统,任意网址打包成小程序
- js利用AXUI框架搭建登录,注册,且完成登录和注册服务器请求
- 普中STM32-PZ6806L开发板(使用过程中的问题收集)
- 使用逃逸分析-进行代码优化
- VLPOD 产生的物料凭证 的移动类型都是101,但是实际业务有其他的移动类型,如何修改移动类型呢
- 提升用户体验的秘密武器!4款UI动效软件推荐,助力你的设计脱颖而出!
- 今年CV顶会上这个方向最火!