TIMESNET: TEMPORAL 2D-VARIATION MODELINGFOR GENERAL TIME SERIES ANALYSIS

引言

This paper was published as a conference paper at ICLR 2023

实现任务通用是深度学习基础模型研究的核心问题，也是近期大模型方向的主要关注点之一。

然而，在时间序列领域，各类分析任务的差别较大，既有需要细粒度建模的预测任务，也有需要提取高层语义信息的分类任务。如何构建统一的深度基础模型高效地完成各类时序分析任务，此前尚未有成型方案。

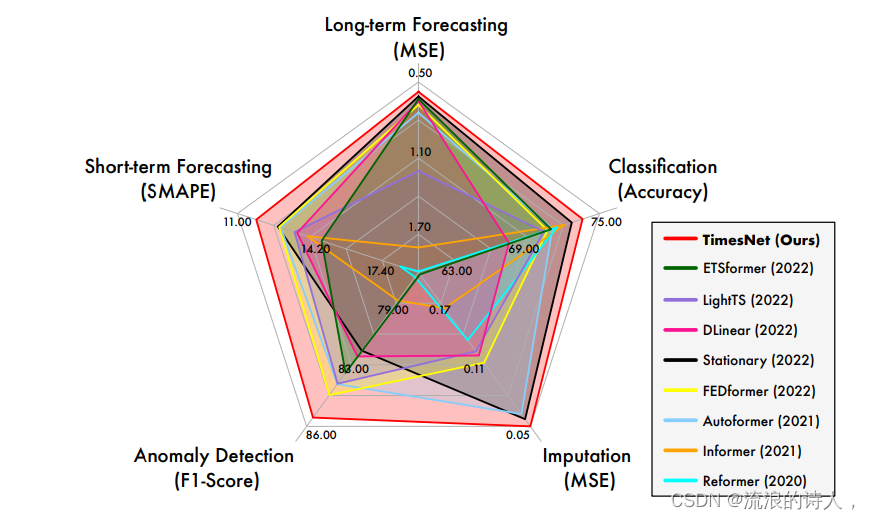
为此，来自清华大学软件学院的团队围绕时序变化建模这一基本问题展开研究，提出了任务通用的时序基础模型TimesNet，论文被ICLR 2023接收。TimesNet在长时、短时预测、缺失值填补、异常检测、分类五大任务上实现了全面领先。

1 问题分析

不同于自然语言、视频等序列数据，时间序列中单个时刻仅保存了一些标量，其关键信息更多地被蕴含在时序变化（Temporal Variation）中。

因此，建模时序变化是各类时序分析任务共同的核心问题。

近年来，各类深度模型被广泛用于时序分析任务中，例如循环神经网络（RNN）、时序卷积网络（TCN）和变换器网络（Transformer）。

然而，前两类方法主要关注捕捉临近时刻之间的变化，在长期依赖上建模能力不足。

Transformer虽然在建模长期依赖上具有天然优势，但是由于现实世界的时序变化极其复杂，仅仅依靠离散时间点之间的注意力（Attention）难以挖掘出可靠的时序依赖。

为此，本文从一个全新的多周期（Multi-periodicity）视角对时序变化进行了分析，如下图所示。我们观察到：

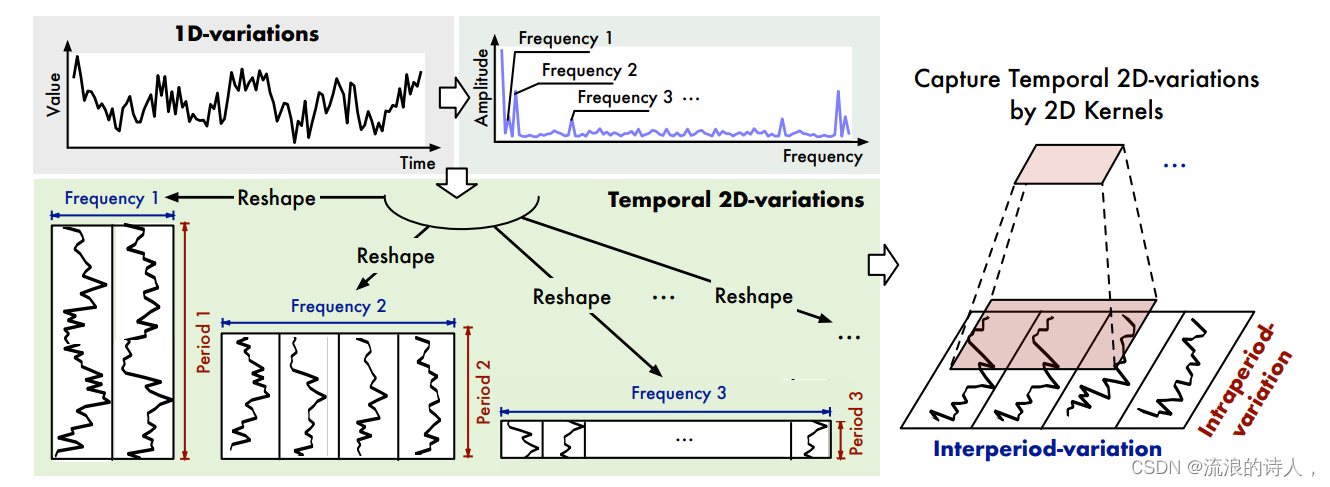
?图1：时间序列的多周期性和时间二维变化。每个周期都包含周期内和周期间变化。我们将原始的一维时间序列转换为一组基于多个周期的二维张量，可以统一周期内和周期间的变化。

• 时间序列天然具有多周期性。现实世界的时序数据往往是不同周期过程的相互叠加，例如交通数据在短期内的以日为周期变化，而长期则以星期为周期变化。这些不同周期的数据互相叠加、互相干扰，给时间序列分析带来了极大挑战。
• 时间序列呈现周期内与周期间两种时序变化。 对于某一特定周期过程，其内部每个时间点的时序变化不仅仅与临近时刻有关，也与邻近周期高度相关，即呈现周期内（Intraperiod-）与周期间（Interperiod-）两种时序变化。其中周期内变化对应着一个周期内的短期过程，周期间变化则可以反应连续周期间的长期趋势。

注：如果数据没有明显的周期性，则时序变化被周期内变化主导，等价于周期长度无穷大的情况。

2 设计思路

???基于以上两点观察，我们对TimesNet的结构作出了如下设计：

?1.时间序列的多周期性自然地启发了一个模块化（Modular）的设计思路，即一个模块捕捉由某一特定周期主导的时序变化。这种模块化的设计思路可以将复杂的时间变化解耦，从而有利于后续建模。

2.对于时间序列的周期内与周期间变化，本文创新性地提出将一维时序数据扩展至二维空间进行分析。如上图所示，将一维时间序列基于多个周期进行折叠，可以得到多个二维张量（2D tensors），每个二维张量的列和行分别反应了周期内与周期间的时序变化，即得到了二维时序变化（Temporal 2D-variations）。

上图示例展示了将一维时序数据折叠至二维空间的可视化效果。此处，Period方向反应周期内变化，而Frequency方向代表周期间变化。我们可以看出转化至二维空间的时序数据具有明显的二维局部性（2D locality）。

因此，在折叠时序数据后，我们可以直接采用先进的视觉骨干网络对时序数据进行特征提取，例如Swin Transformer、ResNeXt、ConvNeXt等。这种设计也使得时序分析任务可以直接受益于蓬勃发展的计算机视觉领域。

3 TimesNet

? ? 基于上述思路，我们提出了TimesNet模型，通过模块化结构将复杂时序变化分解至不同周期，并通过将原始一维时间序列转化至二维空间实现了周期内与周期间变化的统一建模。

在这一节中，我们将先介绍将时序数据扩展至二维空间的方法，再介绍模型的整体架构。

3.1 时序变化：1D->2D

? ?

? 图二：说明时间序列中二维结构的单变量示例。通过发现周期性，我们可以将原始的一维时间序列转换为结构化的二维张量，二维核可以方便的对其进行处理。通过对时间序列的所有变量相同的重塑操作，我们可以将上述过程扩展到多变量时间序列。

? 还值得注意的是，这种变换给变换后的二维张量带来了两种类型的局限性，即相邻时间点（列，周期内变化）和相邻周期（行，周期间变化）之间的局部性。因此，时间二维变化可以很容易的由二维内核处理。
?

时序折叠的流程如上图所示，主要分为以下两步:

（1）周期提取

对于一个时间长度为、通道维度为的一维时间序列，可以由时间维度的快速傅立叶变换（FFT）直接提取周期信息，即：

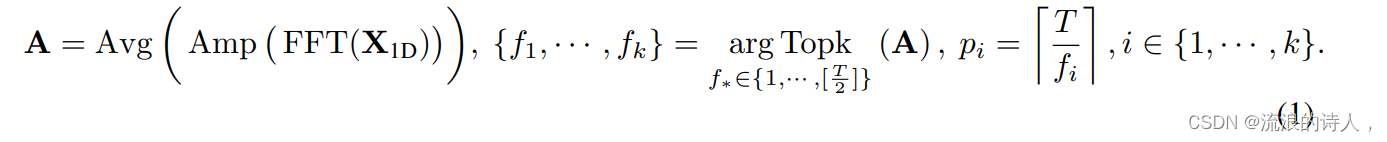
?其中，代表了中每个频率分量的强度，强度最大的个频率对应着最显著的个周期长度。

（2）序列折叠1D->2D

对于选定的个周期，分别对原始的一维时间序列进行折叠，该过程可以形式化为：?

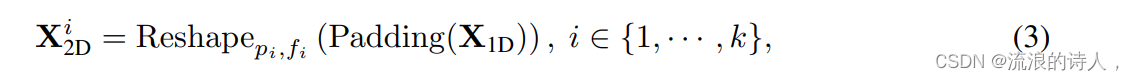
其中，为在序列末尾补0，使得序列长度可以被整除。

通过上述操作，我们得到了一组二维张量，其中对应周期为的二维时序变化。

3.2 模型设计

TimesNet的整体架构如图所示：

?

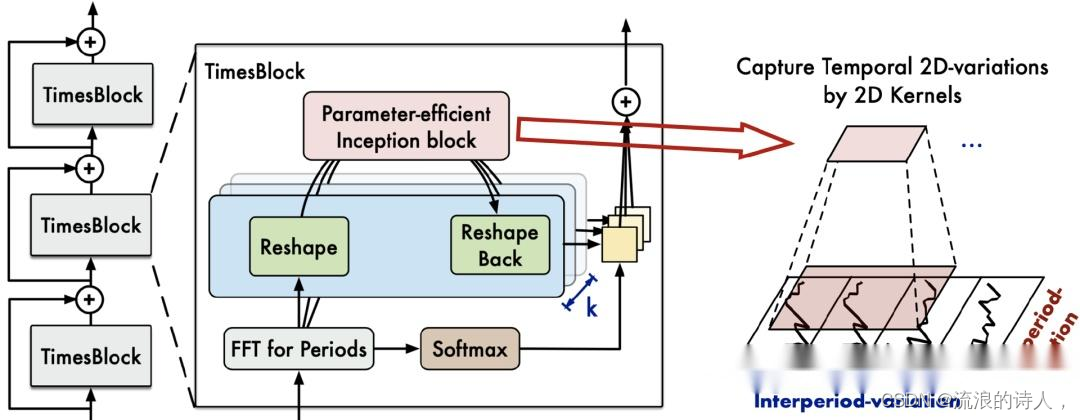
整体上，TimesNet由堆叠的TimesBlock组成。输入序列首先经过嵌入层得到深度特征。对于第层TimesBlock，其输入为，输出为：

?

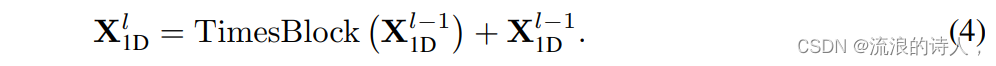
具体地，如下图所示，每个TimesBlock包含以下子过程：

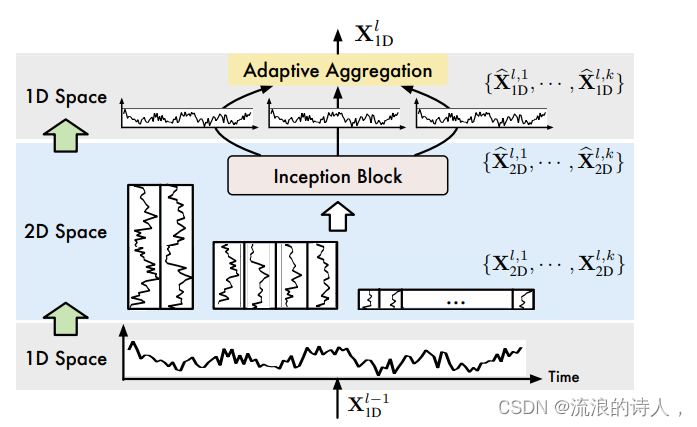
（1）折叠时间序列（1D->2D）：TimesBlock首先对输入的一维时序特征提取周期，再将之转换成为二维时序变化，即在上一节中涉及的内容：

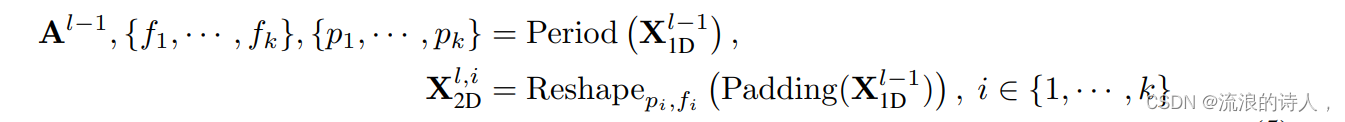
?（2）提取二维时序变化表征（2D Representation）：如前分析，转换得到的二维时序变化具有2D局部性，因此可以直接使用2D卷积提取特征。此处，我们选用了经典的Inception模型，即：

值得注意的是，因为我们已经将1D时序特征转换至2D空间，所以我们还可以利用计算机视觉领域的许多前沿模型，例如ResNeXt、ConvNeXt以及基于Attention的Swin Transformer等等。这使得时间序列分析可以与视觉骨干网络协同并进。

（3）展开时间序列（2D->1D）：为了后续多周期融合，我们将二维时序变化表征展开至一维度空间：

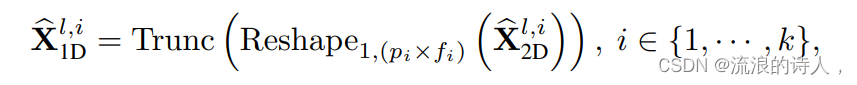
Trunc(?)表示将步骤（1）中Padding(?)操作补充的0去除。

（4）自适应融合（1D Aggregation）：为融合多周期信息，我们将提取到的二维时序表征进行加权求和，选用的求和权重即为步骤（1）中得到的对应频率强度：

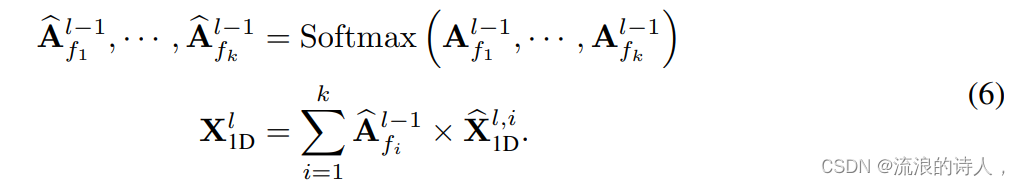
通过将1D时间序列转化至2D空间的设计，TimesNet实现了「多个周期分别提取二维时序变化，再进行自适应融合」的时序变化建模过程。

4 实验

我们在长时预测、短时预测、缺失值填补、异常检测、分类五大任务上进行了实验，涵盖36个数据集、81种不同的实验设置。

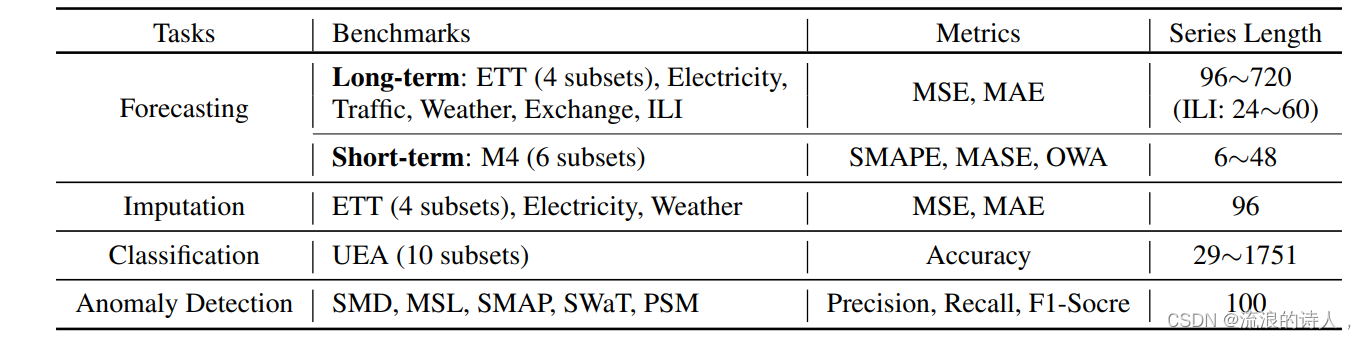
同时，对比了19种不同的深度方法，包含最新的基于RNN、CNN、MLP、Transformer的模型，例如N-BEATS（2019），Autoformer（2021），LSSL（2022），N-Hits（2022），FEDformer（2022），Dlinear（2023）等。

4.1 总体结果

如开篇雷达图所示，TimesNet在五项任务上均达到了SOTA。

（1）长时预测：在此备受关注的任务上，TimesNet超过了先进的基于Transformer与MLP的模型。

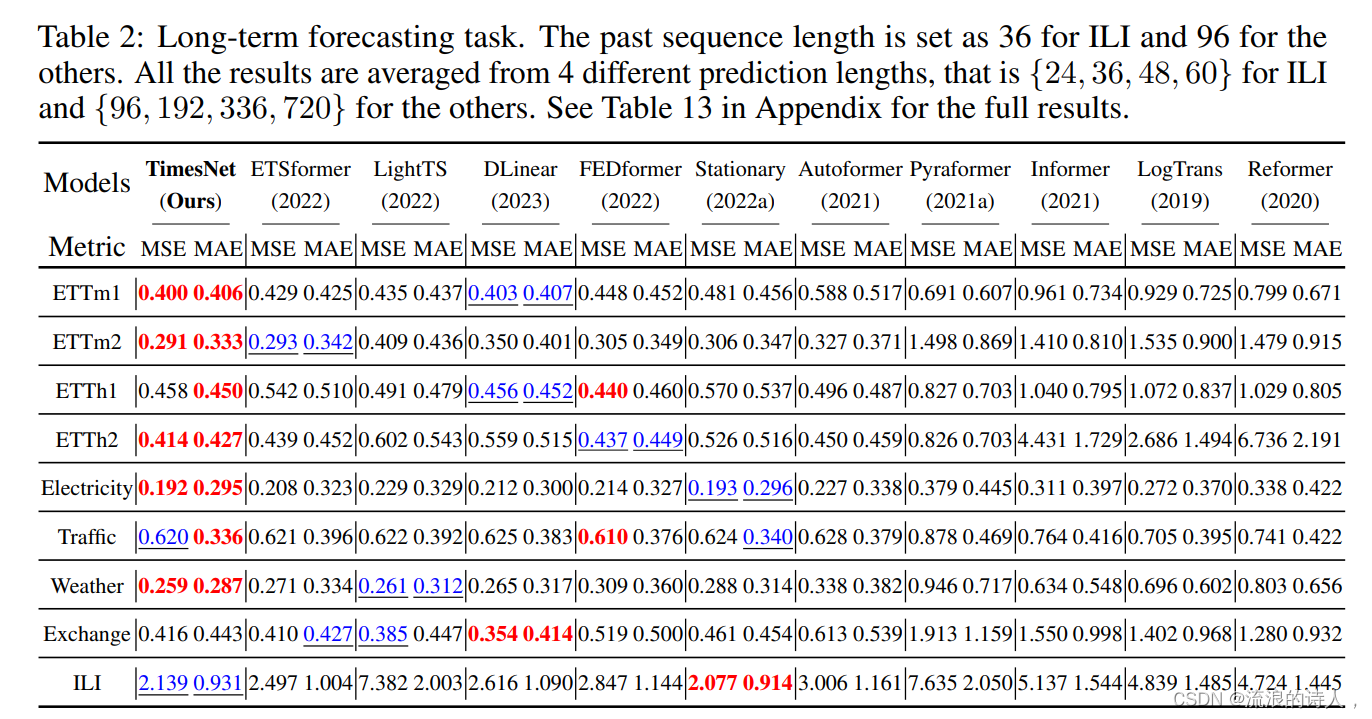
?（2）短时预测：此实验中使用的M4数据集包含6个不同采样频率的子数据集，总共超过10万条数据。TimesNet在此复杂数据分布情况下依然取得了最优的效果，验证了模型的时序变化建模能力。

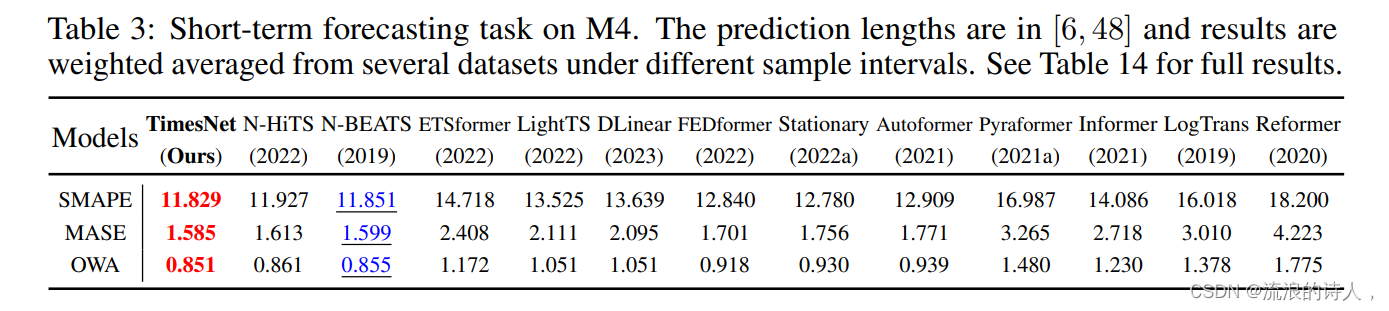
?（3）分类任务：在此任务上，TimesNet超过了经典的Rocket算法以及前沿深度学习模型Flowformer。

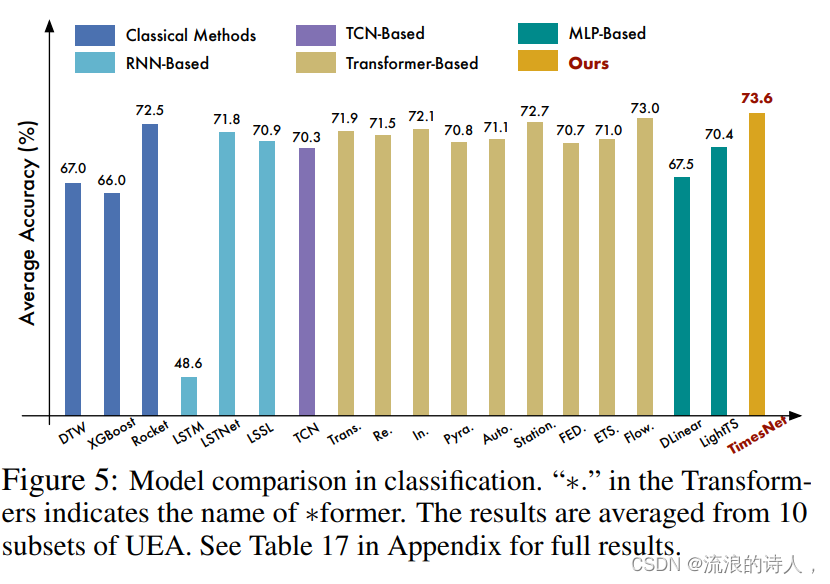
4.2 视觉骨干网络的泛化性?

? 我们将TimesNet中的Inception网络替换为不同的视觉骨干网络，例如ResNet，ConvNext，Swin Transformer等。

? 如下图所示，更先进的视觉骨干网络可以带来更优秀的效果。这也意味着在TimesNet的框架下，时间序列分析可以直接受益于视觉骨干网络领域的进展。

?

我们将TimesNet中的Inception网络替换为不同的视觉骨干网络，例如ResNet，ConvNext，Swin Transformer等。

如下图所示，更先进的视觉骨干网络可以带来更优秀的效果。这也意味着在TimesNet的框架下，时间序列分析可以直接受益于视觉骨干网络领域的进展。

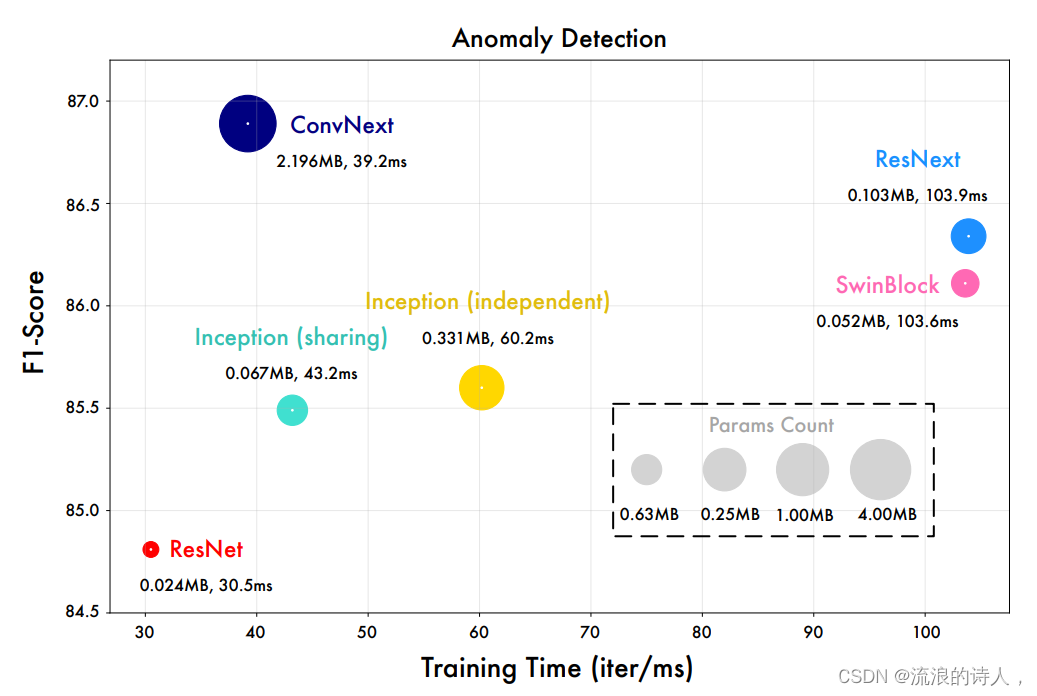
4.3 表征分析

为了进一步探索TimesNet的效果来源，我们展示了「模型底层-顶层表征之间的CKA相似度」与「模型效果”之间的关系。其中，CKA相似度越低，代表模型底层-顶层之间的表征差异越大，即更加层次化的表征。

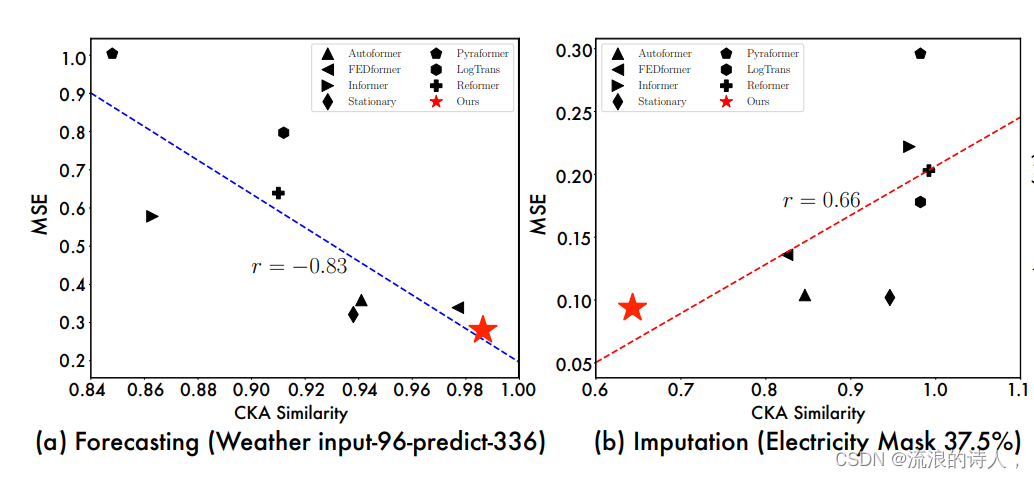
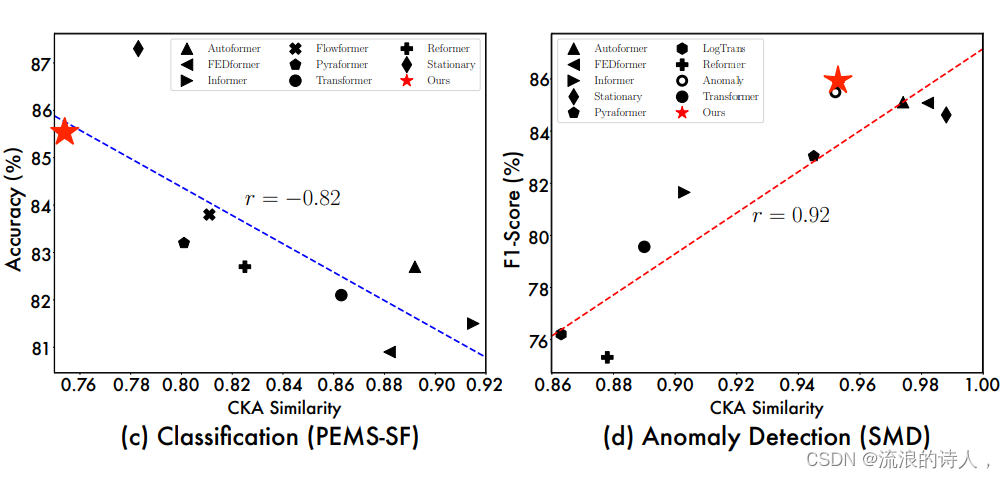?从上述可视化，我们可以观察到：

• 在预测与异常检测任务中，效果越好的模型往往底层-顶层的表征相似度越高，表明任务需要更加底层的表征（low-level representations）；
• 在分类与缺失值填补任务中，效果越好的模型往往底层-顶层的表征相似度越低，表明该任务需要层次化表征（hierarchical representation），即更好的全局特征提取能力。

?得益于2D空间中的卷积操作，TimesNet可以根据不同任务学习合适的表征，例如预测与异常检测任务中，学习到低层次表征；而分类与缺失值填补任务中，学习到层次化的抽象特征。这也进一步证明了TimesNet作为基础模型的任务泛化性。

同时，上述表征分析也为针对专一任务的深度模型提供了设计思路，例如对于预测任务要关注底层细粒度特征的提取，对于填补任务则需要进一步兼顾全局表征的学习。

?

5 总结

? ?受时间序列本质的多周期属性启发，本文提出了一个任务通用的时序分析基础模型——TimesNet。该模型创新性地将一维时间序列折叠至二维空间，并利用2D卷积取时序特征。这一创新使得时序分析任务可以直接受益于蓬勃发展的视觉骨干网络，对于后续研究具有良好的启发性。

? ?同时，TimesNet在长时、短时预测、缺失值填补、异常检测、分类五大主流时序分析任务上实现了全面领先，具有优秀的应用价值。