代码随想录算法训练营29期|day27 任务以及具体安排

// 剪枝优化
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // 先进行排序
        backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
        return res;
    }

    public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
        // 找到了数字和为 target 的组合
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(res, path, candidates, target, sum + candidates[i], i);
            path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素
        }
    }
}

思路：典型的回溯算法，套用回溯三部曲就可以，这道题可以在for循环里面做剪枝操作，if(sum + candidates[i])>target 就终止遍历

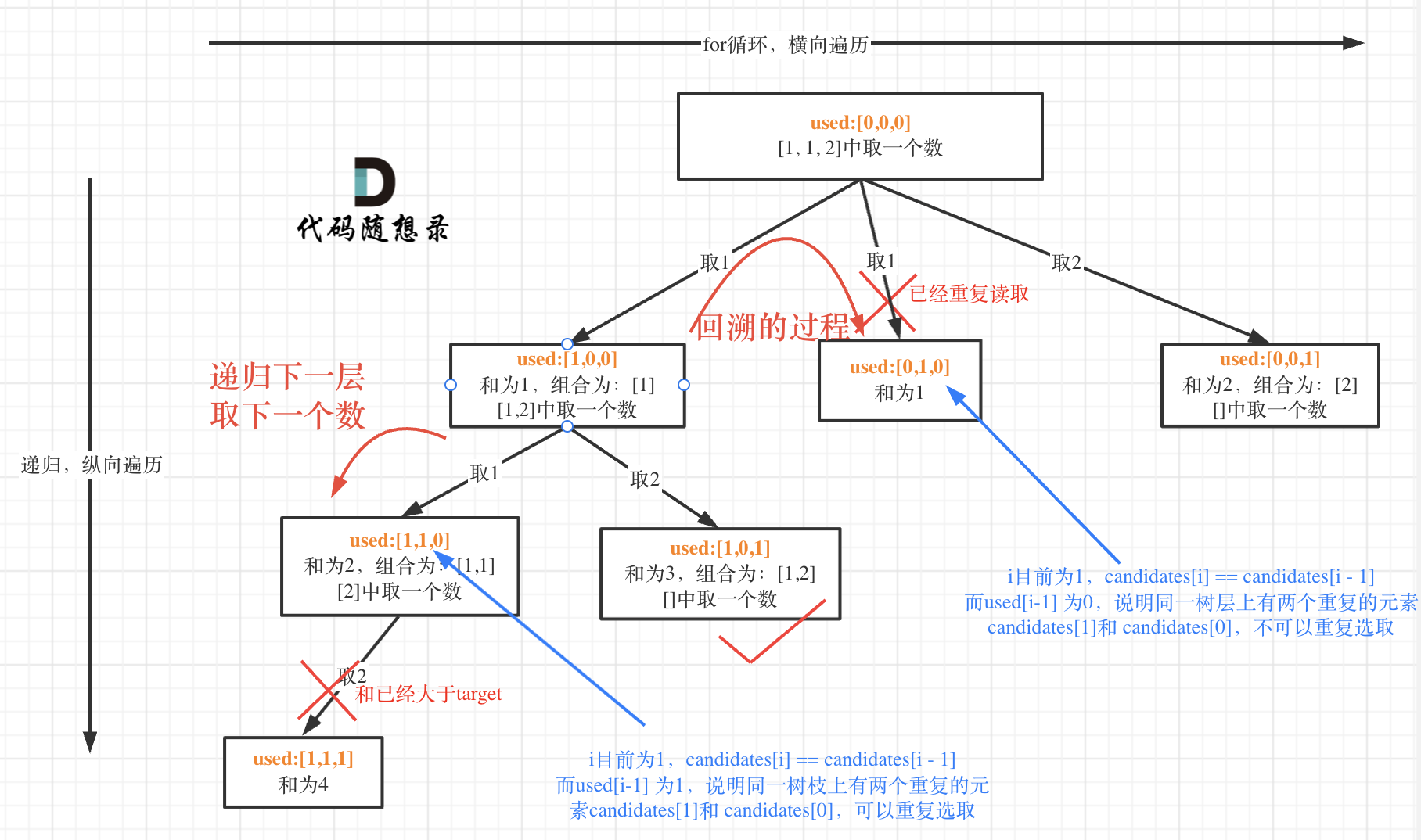
class Solution {
  LinkedList<Integer> path = new LinkedList<>();
  List<List<Integer>> ans = new ArrayList<>();
  boolean[] used;
  int sum = 0;

  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    used = new boolean[candidates.length];
    // 加标志数组，用来辅助判断同层节点是否已经遍历
    Arrays.fill(used, false);
    // 为了将重复的数字都放到一起，所以先进行排序
    Arrays.sort(candidates);
    backTracking(candidates, target, 0);
    return ans;
  }

  private void backTracking(int[] candidates, int target, int startIndex) {
    if (sum == target) {
      ans.add(new ArrayList(path));
    }
    for (int i = startIndex; i < candidates.length; i++) {
      if (sum + candidates[i] > target) {
        break;
      }
      // 出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
      if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
        continue;
      }
      used[i] = true;
      sum += candidates[i];
      path.add(candidates[i]);
      // 每个节点仅能选择一次，所以从下一位开始
      backTracking(candidates, target, i + 1);
      used[i] = false;
      sum -= candidates[i];
      path.removeLast();
    }
  }
}

思路：回溯思路与上题差不多，主要是去重的操作，去重分为树枝去重和树层去重，本题是树层去重，同一层的数据，与前一个数据相等时，去重（跳过），用used[i-1]==false保证是同一层的而不是同一个树枝。

class Solution {
    List<List<String>>result = new ArrayList<>();
    LinkedList<String>path = new LinkedList<>();
    public List<List<String>> partition(String s) {
        backTracking(s, 0);
        return result;
    }

    public void backTracking(String s, int startIndex){
        if(startIndex == s.length()){
            result.add(new ArrayList<>(path));
        }

        for(int i = startIndex ; i < s.length() ; i++){
            if(isPalindrome(s, startIndex, i) == true){
                path.add(s.substring(startIndex, i+1));
            }else{
                continue;
            }

            backTracking(s, i+1);
            path.removeLast();
        }
    }

    public boolean isPalindrome(String s, int startIndex, int endIndex){
        for(int i = startIndex, j = endIndex ; i < j ; i++, j--){
            if(s.charAt(i) != s.charAt(j)){
                return false;
            }
        }
        return true;
    }
}

思路：该题和组合问题类似，主要是要理清startIndex代表分割位置的思想，相当于画线操作，当一个区间为回文串的时候，add进path中，回溯终点是startIndex==s.length()