数据结构与算法python版本之线性结构之栈
什么是线性结构Linear Structure?
线性结构是一种有序数据项的集合,其中每个数据项都有唯一的前驱和后继
除了第一个没有前驱,最后一个没有后继
新的数据项加入到数据集中时,只会加入到原有的某个数据项之前或之后
具有这种性能的数据集,就称为线性结构
线性结构总有两端,在不同的情况下,两端的称呼也不同,有时候称为左右端、前后端、顶端和底端
两端的称呼并不是关键,不同线性结构的关键区别在于数据项增减的方式,有的结构只允许数据项从一端添加,而有的结构则允许数据项从两端移除
我们从4个最简单但功能强大的结构入手,开始研究数据结构,这些结构是:
栈Stack、队列Queue、双端队列Deque和列表list,这些数据集的共同特点在于,数据项之间只存在先后的次序关系,都是线性结构
这些线性结构虽然简单,但是也是应用最为广泛的数据结构
栈Stack:什么是栈?
一种有次序的数据项集合,在栈中,数据项的加入和移除都仅发生在同一端
在日常生活中有很多栈的应用,比如盘子,托盘和书堆等等
所以我们看到,距离栈底越近的数据项,留在栈中的时间就越长,而最新加入的栈的数据项会最先移除
这种次序通常称为“后进先出”LIFO:Last in first out,这是一种基于数据项保存时间的次序,时间越短的离栈顶越近,而时间越长的离栈底越近
栈的特性:反转次序
这种访问次序反转的特性,我们在某些计算机上碰到过,比如说浏览器的后退back按钮,最先back的是最近访问的网页
抽象数据类型栈是一个有次序的数据集,每个数据项仅从栈顶一端加入到数据集中、从数据集中移除,栈具有后进先出的特性
抽象数据类型栈定义为如下的操作:
Stack():创建一个空栈,不包含任何数据项
push(item):将item加入栈顶,无返回值
pop():将栈顶数据项移除,并返回,栈被修改
peek():“窥视”栈顶数据项,返回栈顶的数据项但不移除,栈不被修改
isEmpty():返回栈是否为空栈
size():返回栈中有多少个数据项
我们举一个操作样例的示例
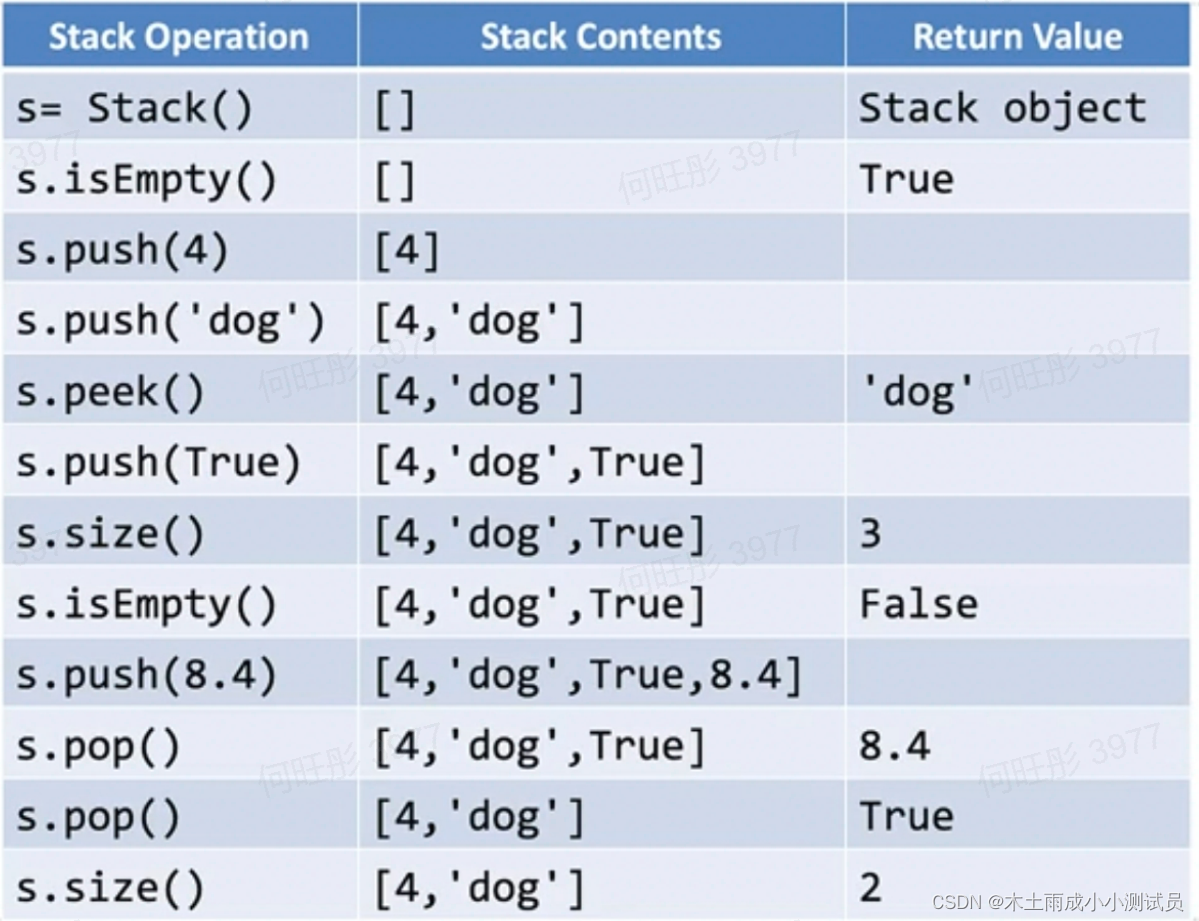
那么我们如何用python实现ADT Stack
Python的面向对象机制,可以用来实现用户自定义类型
将ADT Stack实现为Python的一个Class
将ADT Stack的操作实现为Class的方法
由于Stack是一个数据集,所以可以采用Python的原生数据集来实现,我们选用最常用的数据集List来实现
class Stack:
def _init_(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
ADT Stack的另一个实现
不同的实现方案保持了ADT接口的稳定性,但性能有所不同,栈顶首端的版本(上),其push/pop的复杂度为O(n),而栈顶尾端的实现(右),其push/pop的复杂度为O(1)
class Stack:
def _init_(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.insert(0,item)
def pop(self):
return self.items.pop(0)
def peek(self):
return self.items[0]
def size(self):
return len(self.items)
class Stack:
def _init_(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
栈的应用:简单括号匹配
我们都写过这样的表达式,(5+6)*(7+8)/(4+3),这里的括号是用来指定表达式项的计算优先级;有些函数式语言,在函数定义的时候会用到大量的括号;
当然,括号的使用必须遵循平衡原则,首先,每个开括号恰好要对应一个闭括号,其次,每对开闭括号要正确的嵌套
对于括号是否正确匹配的识别,是很多语言编译器的基础算法
那么,如何构造括号匹配识别的算法呢?
从左到右扫描括号串,最新打开的左括号,应该匹配最先遇到的右括号
这样,第一个左括号(最早打开),就应该匹配最后一个右括号(最后遇到)
这种次序反转的识别,正好符合栈的特性!
#栈的应用
from pythonds.basic.stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
#放到一个栈里面
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
#删除掉最后一个元素
s.pop()
index = index + 1
# print(index)
if balanced and s.isEmpty():
return True
else:
return False
print(parChecker('(())'))
我们在实际的应用里,我们会碰到更多种括号
比如python中列表所用的方括号“[]”
字典所用的花括号“{}”
元组和表达式所用的圆括号“()”
这些不同的括号有可能混合在一起使用,因此就要注意各自的开闭匹配情况。
栈的应用:十进制转换为二进制
二进制是计算机原理中最基本的概念,作为组成计算机最基本部件的逻辑门电路,其输入和输出均仅为两种状态:0和1
但十进制是人类传统文化中最基本的数值概念,如果没有进制之间的转换,人们跟计算机的交互会相当的困难
所谓的进制就是用多少个字符来表示整数,十进制是0-9这十个数字字符,二进制是0和1两个字符;
我们经常需要将整数在二进制和十进制之间转换
十进制转换为二进制
采用的是“除以2求余数”的算法,将整数不断除以2,每次得到的余数就是由低到高的二进制位;除以2的过程,得到的余数是从低到高的次序,而输出则是从高到低,所以需要一个栈来反转次序;
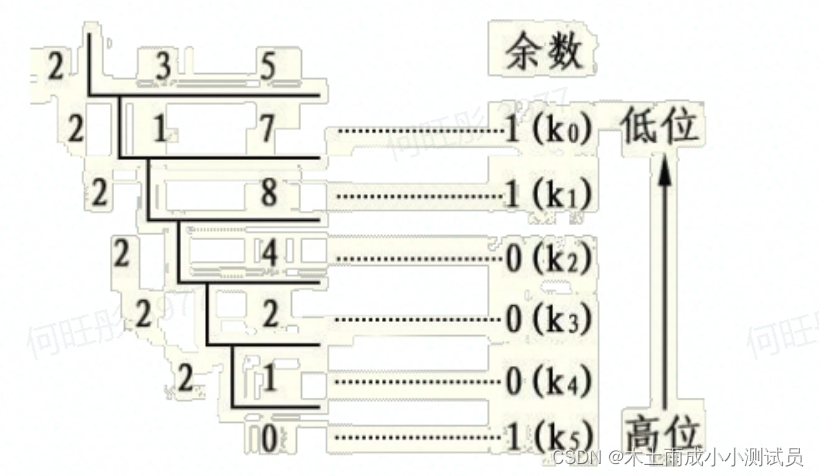
#栈的应用:十进制转换为二进制
from pythonds.basic.stack import Stack
def parChecker(number):
s = Stack()
while number > 0:
#求余数
num = number % 2
#放到栈里面
s.push(num)
#继续除以2
number = number // 2
bstr = ""
while not s.isEmpty():
#使用pop反转
bstr = bstr + str(s.pop())
return bstr
print(parChecker(42))
十进制转换为二级制的算法很容易扩展到转换到任意N进制,只需要将“除以2求余数”的算法改为“除以N求余数”算法就可以
计算机另外两种常用的进制是八进制和十六进制,这个后面大家可以自行研究扩展
表达式转换
中缀表达式:我们通常看到的表达式像这样:BC,很容易知道这个是B乘以C,这种操作符介于操作数中间的表示法,称为“中缀”表示法;但是有时候中缀表示法会引起混淆,如“A+BC”是A+B然后再乘以C,还是B*C然后再去加A?
人们引入了操作符“优先级”的概念来消除混淆
规定高优先级的操作符先计算
相同优先级的操作符从左到右以此计算
这样A+BC就是A加上BC的乘积
同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高
引入全括号表达式:在所有表达式项两边全都加上括号,也就是
A+BC+D应表示为((A+(BC))+D)
前缀和后缀表达式
中缀表达式A+B
将操作符移到前面,变为“+AB”
或者将操作符移到最后,变为“AB+"
我们就得到了表达式的另外两种表示法:前缀和后缀表示法,以操作符相对于操作数的位置来定义
通用的中缀转后缀算法
我们来讨论下通用的中缀转后缀算法,首先我们看下中缀表达式A+BC,其对应的后缀表达式是ABC+:
由此可见,
ABC的操作顺序没有改变;操作符的出现顺序在后缀表达式中反转了;由于*的优先级比+高,所以后缀表达式中操作符出现的顺序与运算次序一致
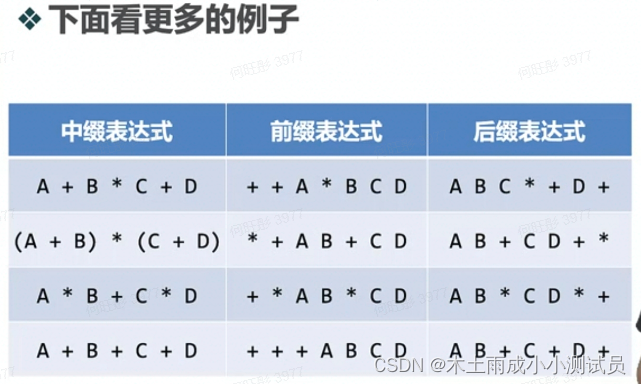
在中缀表达式转换为后缀表达式的处理过程中,操作符比操作数要晚输出:所以在扫描到对应的第二个操作数之前,需要先把操作符先保存起来,而这些暂存的操作符,由于优先级的规则,还有可能要反转次序输出,在A+BC中,+虽然先出现,但优先级比后面这个要低,所以它要等*处理完后,才能再处理。
这种反转特性,使得我们考虑用栈来保存暂时未处理的操作符
总结下,在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符,这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理。
# #栈的应用:表达式转换
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
#记录操作符优先级
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
#解析表达式到单词列表
tokenList = infixexpr.split()
for token in tokenList:
#操作数括号的处理
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == "(":
opStack.push(token)
elif token == ")":
topToken = opStack.pop()
while topToken != "(":
postfixList.append(topToken)
topToken = opStack.pop()
else:
#操作符的处理
while (not opStack.isEmpty()) and (prec[opStack.peek()]) >= prec[token]:
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
#合成后缀表达式字符串
return "".join(postfixList)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Qt开发用到的英文词及其解释
- 中期国际1.22黄金市场分析:美联储考虑放松货币政策,金价会下跌吗?
- 20231217在Canonical 官网下载ubuntu-20.04.6以及通过rufus-4.3p写入U盘作为安装盘
- Jmeter实现服务器端后台接口性能测试!
- VditoreMarkdown编辑器使用
- 16-Kafka Broker
- AI国际顶会ICLR 2024结果揭晓,蚂蚁集团11篇论文入选
- java进阶四-深入理解泛型和注解
- 卷积神经网络和深度神经网络的区别与联系
- Apifox 1月更新:性能测试、多人协作接口实时同步功能全面解析