【强化学习的数学原理-赵世钰】课程笔记(五)蒙特卡洛方法
目录
1.将策略迭代转换为无模型迭代(Convert policy iteration to be model-free)
四.更高效地使用数据(Use data more efficiently):MC Exploring Starts
五.MC 没有探索就启动(MC without exploring starts):Algorithm: MC ε-Greedy
?一.内容概述
- 上节课介绍了 model-base 的方法,这节课将介绍 model-free 的方法,上节课的 policy iteration 的方法是这节课的基础,我们把 policy iteration 当中基于模型的部分替换成不需要模型的部分就得到了今天的算法
- 在这门课中,把 value iteration 和 policy iteration 统称为 model-base reinforcement learning,但是更准确来说,它们应该称为动态规划(dynamic programming)的方法。model-base reinforcement learning 简称?MBRL,这个研究的是我用数据估计出一个模型,再基于这个模型进行强化学习。
课程大纲:
1.激励性实例(Motivating examples):介绍蒙特卡洛估计(Mento Carlo Estimation)的基本思想
2.介绍三个基于蒙特卡洛(MC)强化学习的算法(这三个算法环环相扣,前一个是后一个的基础)
(1)最简单的基于 MC 的 RL 算法:MC basic
(2)更高效地使用数据:MC Exploring Starts
(3)MC 没有探索就启动:Algorithm: MC ε-Greedy

二.激励性实例(Motivating examples)
- 我们如何在没有模型的情况下去估计一些量?(How can we estimate something without models)
- 最简单的方法:蒙特卡洛估算(Monte Carlo estimation)。
下面通过一个例子说明蒙特卡洛估算:投掷硬币
投掷硬币后的结果(正面或背面朝上)用随机变量(random variable) X 表示
- 如果结果为正面朝上,则 X = +1
- 如果结果是背面朝上,则 X = -1
目的是计算 E[X](X 的平均数,X 的期望)。
这里有两种方法计算期望
方法 1 :基于模型的(model-based)
假设概率模型为(我们知道随机变量(random variable) X 的概率分布(probability distribution)):正面朝上和背面朝上的概率都是 0.5
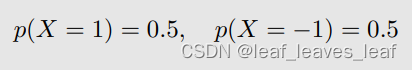
那么随机变量(random variable) X 它的期望(expectation)就可以简单的通过定义计算:
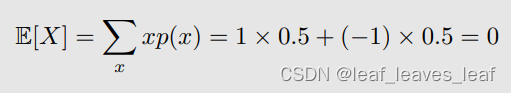
问题:可能无法知道精确的概率分布情况(precise distribution)!!
方法 2?:无模型的(model-free)
基本思想:多次掷硬币,做很多次实验,得到很多的采样,然后计算所有采样的平均结果。
假设我们做了 N 次实验,这 N 次的实验结果分别是 x1,x2,...,xN,得到一个样本序列: {x1, x2, . , xN }。那么,均值可以近似为:

期望(expectation)用???来近似,认为??
?是 E(X)
这就是蒙特卡洛估计的基本思想!
问题:用蒙特卡洛估计(Mento Carlo Estimation)是否精确?
- 当 N 较小时,近似值不准确。
- 随着 N 的增大,近似值会越来越精确。
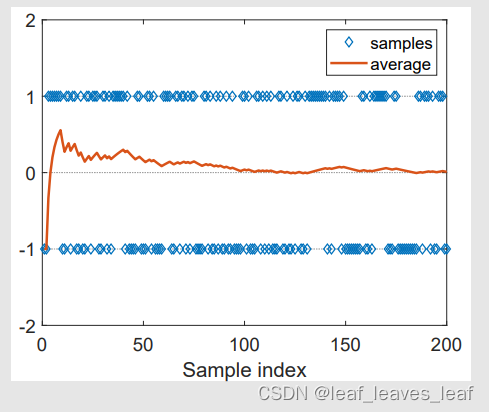
如上图所示,我们已知真实的期望(expectation)是 0,随着做平均的样本数越多,样本的平均值(expectation)越接近真实的期望(expectation)0
上面这样直观的解释有数学理论做支撑(大数定律)
iid:独立同分布样本(independent and identically distributed sample)

总结:
- 蒙特卡罗估计是指依靠重复随机抽样来解决近似问题的一大类技术。凡是需要做大量的采样实验,最后用实验的结果近似的的方法,都可以称为蒙特卡洛估计的方法。
- 我们为什么要关注蒙特卡罗估计?因为它不需要模型!
- 为什么要关注均值估计(mean estimation)?为什么用蒙特卡洛来估计期望(expectation)?因为状态值(state value)和行动值(action value)被定义为随机变量的期望值(expectation)!
三.最简单的基于 MC 的 RL 算法:MC basic
1.将策略迭代转换为无模型迭代(Convert policy iteration to be model-free)
理解算法的关键是理解如何将策略迭代算法(policy iteration algorithm)转换为无模型算法(model-free)。我们知道策略迭代算法(policy iteration algorithm)是依赖于模型的,但是实际上我们可以把它依赖于模型的那部分给替换掉,替换成 model-free 的模块
- 应充分理解策略迭代(policy iteration algorithm)。
- 应理解蒙特卡罗均值估计(Monte Carlo mean estimation)的思想。
接下来看策略迭代算法(policy iteration algorithm)如何转换为无模型(model-free)的:
策略迭代(policy iteration algorithm)的每一次迭代都有两个步骤:
- 1.策略评估:我有一个策略?πk,通过求解贝尔曼公式,我要求出来它的状态值(state value)v_πk
- 2.策略改进:知道?v_πk 之后就可以做改进,求解一个最优化问题得到一个新的策略?πk+1。(通过选择最大的 q_πk 得到新的策略?πk+1)

这里面非常核心的量是 q_πk (s, a)
要计算动作值(action value) q_πk (s, a) 有两种算法:
方法 1 需要模型:这就是 value iteration 这个算法所使用的,第一步得到了?v_πk,第二步这些概率模型都是知道的,所以就可以求出来 q_πk (s, a)

方法 2 不需要模型:这种方法依赖于动作值(action value) q_πk (s, a) 最最原始的定义。就是从当前状态 s 出发,选择动作 a 之后,我所得到的回报(return),这个 return 是一个随机变量,我求它的平均(average)或者求期望(expectation)就是动作值(action value)

上面这个式子是基于蒙特卡洛方法的核心思想,这是一个均值估计(mean estimation)的问题,在第一部分(motivating example)中介绍了蒙特卡洛估计(Monte Carlo estimation)可以用来解决均值估计(mean estimation)的问题
实现无模型 RL 的思路:我们可以使用方法?2 的表达式,根据数据(样本或经验)计算 q_πk(s,a)!

下面来看一下具体是怎么求解的:
动作值(action value)的蒙特卡洛估计(Monte Carlo estimation)程序:

- 从 (s,a) 开始,根据当前的策略 πk ,得到一个?episode( 在第一章中介绍了:当智能体按照策略(policy)与环境交互时,可能会在某些终端状态(terminal states)停止。由此产生的轨迹(trajectory)称为一集(an episode)(或一次试验 trail))
- 计算出来这个 episode 对应的折扣回报(discounted return)g(s,a)
- Gt 是一个随机变量(random variable),g(s,a) 是这个随机变量 Gt 的一个采样

- 如果我们有很多这样的采样,有一个集合,我们就可以用这些采样 g 求一个平均值,来估计 Gt? 的这个平均值,就是估计 Gt 的期望(expectation)。这个就是蒙特卡洛估计(Monte Carlo estimation),刚才在第一部分 motivating example 中介绍的

基本理念: 当模型不可用时,我们可以使用数据。(没有模型就要有数据,没有数据就要有模型)(Fundamental idea: When model is unavailable, we can use data. )这里的数据在统计或者是概率里面叫样本(sample),在强化学习中它有一个特殊的名字叫经验(experience)
2.The MC Basic algorithm
到此为止,算法已经逐渐清晰了,这个算法的名字叫:MC Basic algorithm,MC是蒙特卡洛首字母的缩写
算法描述:

伪代码:

- MC Basic 是策略迭代算法(policy iteration algorithm)的一种变体,就是把基于 model 的模块拿掉,换成一个不需要 model 的模块。
- 无模型算法是在基于模型算法的基础上建立起来的。因此,在研究无模型算法之前,有必要先了解基于模型的算法。
- 要学习基于蒙特卡洛的强化学习的算法,首先应该明白基于模型的?policy iteration 的算法
- MC Basic 有助于揭示基于 MC 的无模型 RL(MC-based model-free RL)的核心思想,MC Basic 有助于揭示如何把 model-base 变成 model-free 的过程,但由于效率低(low efficiency)而不实用,之后还会介绍两个算法提高效率(efficiency)。
- 既然策略迭代(policy iteration algorithm)是收敛的,那么 MC Basic 的收敛性也是有保证的,因为他俩类似,只是估计 action value 的方法有些差别。
为什么 MC Basic 估算的是动作值而不是状态值?MC Basic 是直接来估计动作值(action value),而在 policy iteration 中是先估计了 state value,再转成 action value
- 这是因为如果要估计 state value,之后还要转成 action value,那从 state value 到 action value 又依赖于模型,这是不行的,所以要直接把 action value 估计出来。状态值不能直接用于改进策略,当没有模型时,我们应该直接估计行动值。
3.例子
(1)例子 1
在下面的例子中,有一个初始策略?π0(图中绿色箭头),在其他状态策略不错,只是在状态 s1,s3 策略不太好。接下来就从?π0 出发,用 MC Basic 算法找到一个最优的策略。

大纲:给定当前策略?πk
步骤1:策略评估(policy evaluation):对任意的 s 和任意的 a,计算 q_πk (s, a)
- 在这个例子中有 9 个 state,每个 state 对应 5 个 action,有 45 个 state-action pairs,所以要找到 45 个 q_πk (s, a),假设从每一个(s,a)出发都有 N 条轨迹,最后要求 N 条轨迹的平均的 return,那么一共有 45 × N 条轨迹。
步骤2:策略改进(policy improvement)
- 在每个状态求出哪个 action 对应最大的 action value,就选择那个 action

由于篇幅有限,我们不可能把 45 个 q_πk 全部找到,我们只找 5 个,针对 s1 它的 5 个 action,只展示 qπk (s1, a):
步骤1:策略评估(policy evaluation):
- 刚才提到,如果我从一个(s1,a1)出发的话,要找 N 个轨迹,对这 N 条轨迹的 return 求平均,这样才能求出 q_πk(s1,a1)。但是由于当前的问题很简单,当前的策略(policy)是确定性的(deterministic),当前的环境也是确定性的(deterministic),也就意味着,如果我从一个(s1,a1)出发,不管采样多少次,最后得到的轨迹都是相同的,因此只采样一次就可以,因此只需 one episode 就能得到行动值!
- 如果在更复杂的情况下,policy 是随机的(stochastic);或者策略(policy)是确定性的(deterministic),但是环境是随机的(stochastic)。那么如果我从一个(s1,a1)出发,采样不同次就会得到不同的轨迹,那么就需要无限多的事件(episodes)(或至少很多事件(episodes))!需要采样多次,然后求一个平均


步骤2:策略改进(policy improvement)
比较一下?q_πk 对应的 action value 哪个最大,这里 a2,a3 最大

因为他俩对应的 action value 是一样的,所以可以任意选择 a2,a3 作为一个新的策略

s1 的这个新策略已经实现最优了,对于这个简单的例子,一个 iteration 就可以找到实现它的最优策略。这是因为除了 s1 之外,s1 周围的其他 state 已经达到最优了,所以 s1 也可以轻松找到最优策略。
(2)例子2
这个例子不是展示如何用 MC basic 解决一个问题而是假如已经用 MC Basic 得到了一个最优策略,分析一下这个最优策略有什么性质
研究 episode 长度的影响(Examine the impact of episode length):
- 在用 MC Basic 的时候需要数据,这个数据就是从任何一个状态和动作出发,有很多 episode,计算 episode 的 return。这个 episode 的长度理论上是越长越好,计算的 return 越精确,但现实中不能无限长,
- 那么 episode 的长度应该设置为多长才合适?
例子设置:
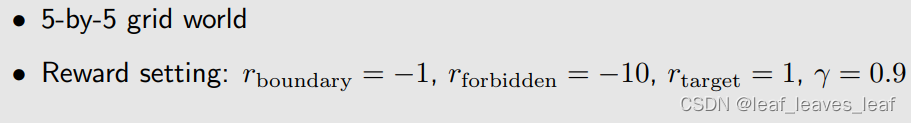
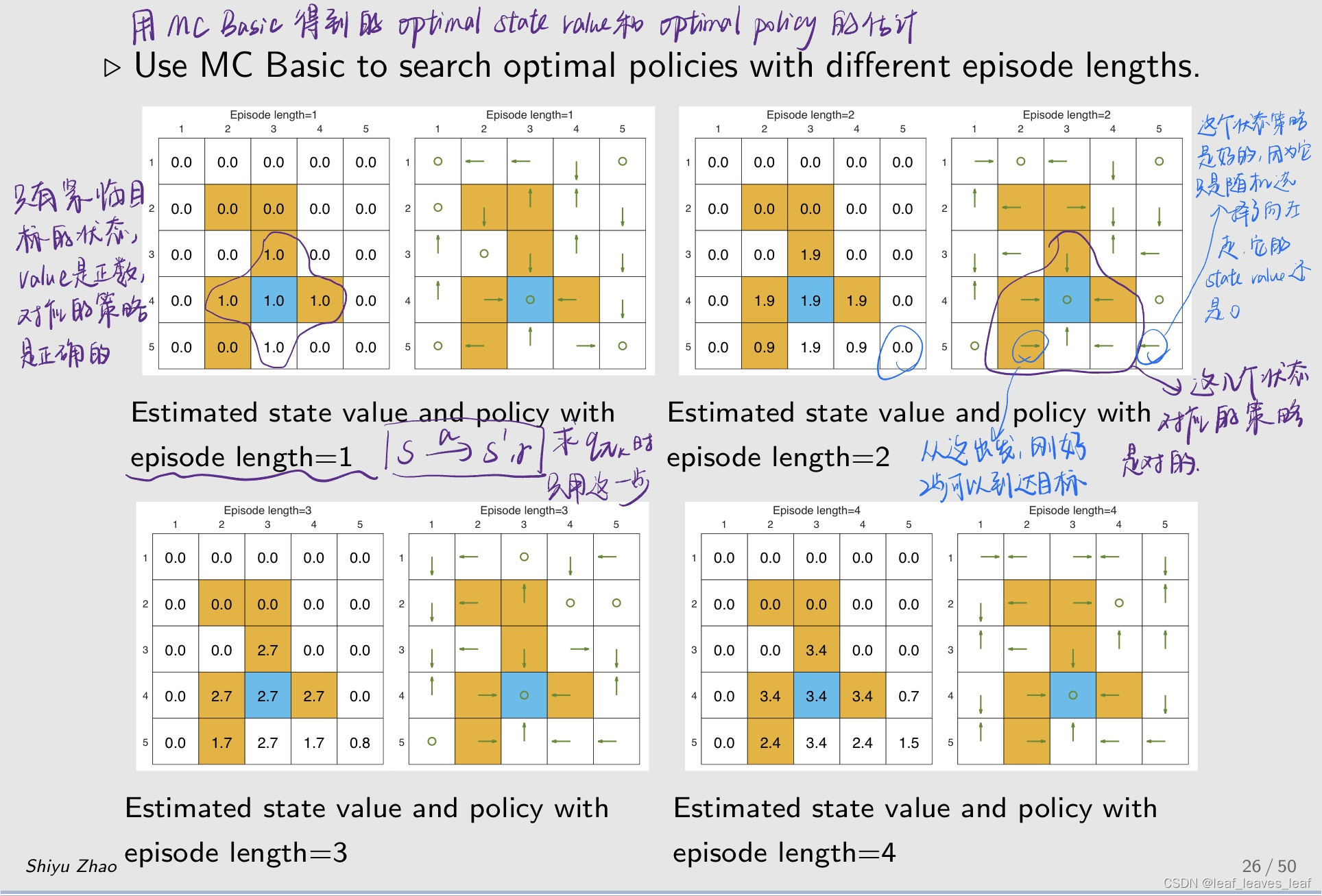
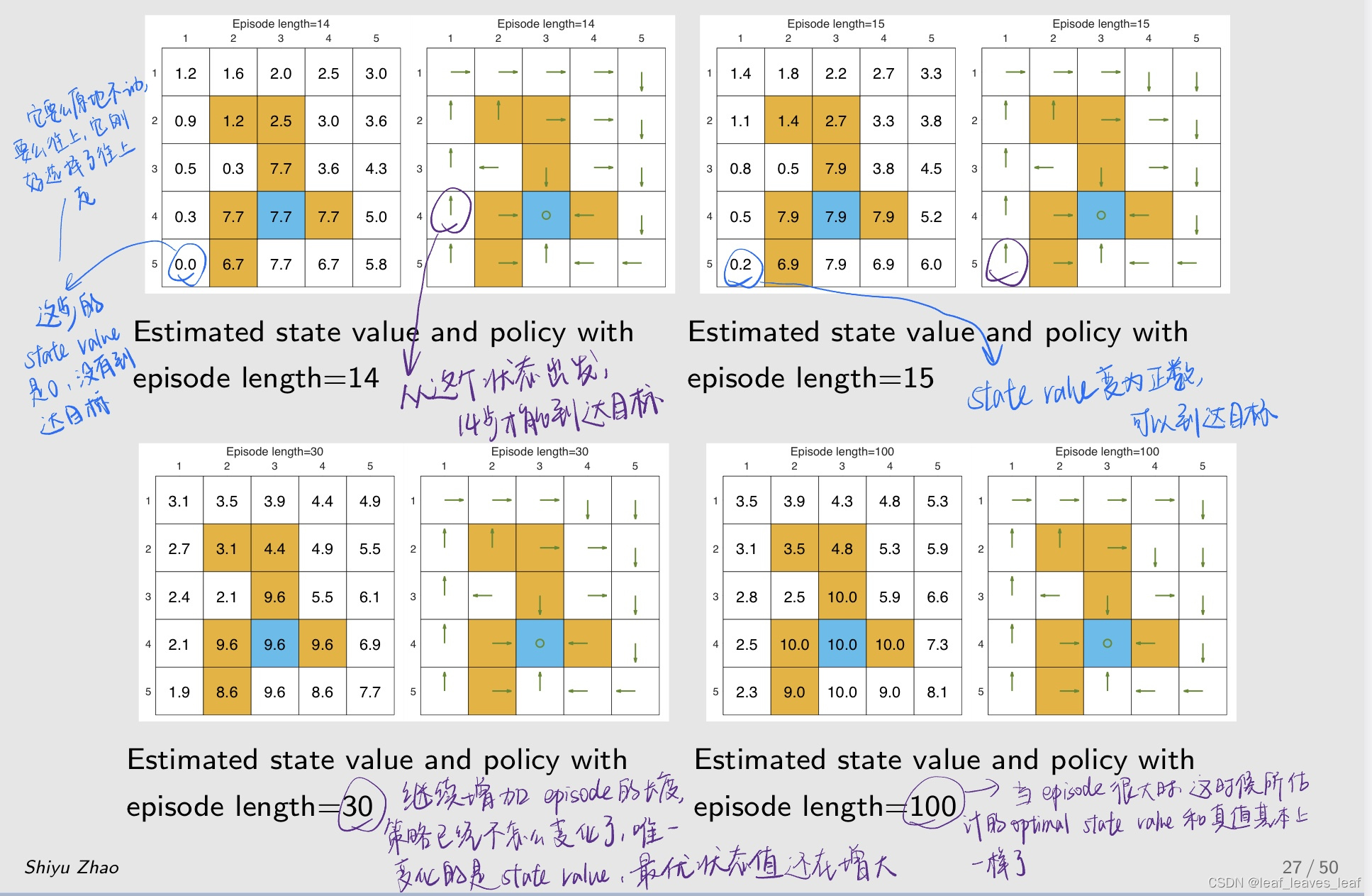
研究结果
- 当 episode 的长度较短时,只有靠近目标的状态具有非零状态值,只有离目标比较近的状态才能在这么短的步骤内找到目标,因此这些状态能找到最优策略。
- 随着 episode 的长度逐渐增加,离目标越来越远的状态也能慢慢到达目标,从而找到最优策略。距离目标较近的状态比距离目标较远的状态更早出现非零状态值。
- episode 的长度应足够长,让所有状态都能有机会到达目标。
- episode 的长度不一定要无限长,充分长就够了。
四.更高效地使用数据(Use data more efficiently):MC Exploring Starts
这个算法是 MC Basic 的推广,可以让算法变得更加高效
MC Basic 算法:
- 优点:清晰揭示核心思想!帮助我们理解怎么样用蒙特卡洛方法实现不需要模型的强化学习
- 缺点:过于简单,不实用,效率低。
- 不过,MC Basic 可以扩展得更有效。
考虑一个网格世界的例子,按照策略 π,我们可以得到 an episode,例如

访问(Visit):每当 episode 中出现一个状态-动作对(state-action pair)时,就称为对该状态-动作对的一次访问。
在 MC Basic 中使用数据的方法:初始访问法(Initial-visit method)
- 对于上图的策略,只考虑(s1,a2),用剩下的得到的 return 来估计(s1,a2)的 action value。只需计算回报值并近似计算 qπ(s1, a2)。
- MC Basic 算法就是这么做的。
- 缺点:不能充分利用数据,有很多数据被浪费了。
如何高效使用数据呢?

数据效率高的方法有两种:
first-visit method:上图中,状态-动作对 (s1,a2) 访问了两次,而?first-visit method 只使用第一次访问?(s1,a2) 的后面来估计 (s1,a1),第二次出现的时候就不用它后面的来进行估计了。
every-visit method:上图中,状态-动作对 (s1,a2) 访问了两次(第一次和第三次),every-visit method 只要访问了,不管是第几次,都可以用它后面的 return 估计 (s1,a2) 的 action value
除了让数据的使用更加高效之外,我们还可以更加高效的去更新策略。基于 MC 的 RL 的另一个方面是何时更新策略。也有两种方法:
第一种方法是,在策略评估(policy evaluation)步骤中,收集从一个状态-行动对(state-action pair)出发的所有 episode,然后使用平均回报(average return)来近似估计动作值(action value)。
- 这是 MC Basic 算法所采用的方法。
- 这种方法的问题在于,智能体必须等到(wait until)所有 episode 都收集完毕。这个等待的过程浪费时间,效率低。
第二种方法是,使用单个 episode 的回报(return)来立刻估计动作值(action value),然后不要等待,下一步就直接开始改进策略。这样的话,我得到一个 episode 就改进策略,得到一个 episode 就改进策略,效率会提升。
- In this way, we can improve the policy episode-by-episode.
第二种方法会产生问题吗?
- 有人可能会说,单个 episode 的回报(return)无法准确地估计出相应的动作值(action value)。
- 事实上,在上一章介绍的截断策略迭代算法(truncated policy iteration algorithm)中,我们已经做到了这一点,在?truncated policy iteration algorithm 中的第一步做的是 policy evaluation,在那一步中要求出当前策略的 state value,求?state value 要求解贝尔曼公式,又需要无穷多步迭代,当时在那个算法中我们只做有限步迭代,虽然得不到非常精确的 state value,但这个算法仍然可行。与现在这个思想类似,用一个 episode 来估计动作值(action value),这显然是不精确的,但是没关系。
这一些方法有名字,叫做?Generalized policy iteration(简称 GPI)
- GPI 不是一种特定的算法,是一大类算法,是一种思想,架构。
- 它指的是在策略评估(policy-evaluation)和策略改进(policy-improvement)过程之间切换的总体思路或框架。而且策略评估(policy-evaluation)不需要非常精确的把?action value 或者?state value 估计出来。
- 许多基于模型和无模型的 RL 算法都属于 GPI 这一框架。上节课和这节课的算法都可以属于 GPI 框架。
有了上面的这些思考,如果我们能更高效地利用数据和更新估计值,就能得到一种新算法,即 MC Exploring Starts,这是我们之前学的 MC Basic 的推广
If we use data and update estimate more efficiently, we get a new algorithm called MC Exploring Starts:

什么是探索起始(exploring starts)?
- 探索(exploring)指的是我从每一个(s,a)出发,都要有 episode,只有这样我才能用后面生成的这些 reward 来估计 return,进一步估计 action value。如果恰恰有一个 state-action 没有被访问到,那我就可能把这个 action 给漏掉了,但是那个可能就是最优的,所以我们需要确保每个都被访问。
- 起始(starts)意味着我们要访问每个(s,a),从它后面能够生成 reward 的这些数据有两种方法:第一种方法是从每一个?(s,a) 开始都有一个 episode,就是 start;第二种方法是从其他的 (s,a) 开始,但是也能经过当前的这个 (s,a),那后面的这些数据也可以估计当前 (s,a) 的 return,这个叫 visit。目前来讲,visit 方法没法确保,它依赖于策略和环境,没法确保从其他的 (s,a) 开始一定能够经过剩下的所有 (s,a),下面我们介绍的新方法就是使得 visit 可以做到,这样就可以避免必须从每个 (s,a) 都开始的条件。
- MC Basic 和 MC exploring starts 都需要这一假设。

为什么我们需要考虑探索起始(exploring starts)?
- 从理论上讲,只有对每个状态(state)的每个动作值(action value)都进行了充分的探索,我们才能正确地选择最优动作(optimal actions)。相反,如果没有探索某个动作,这个动作可能恰好是最优动作,从而被错过。
- 在实践中,探索起始(exploring starts)是很难实现的。对于许多应用,尤其是涉及与环境物理交互的应用,很难收集到从每一对状态-行动开始的 episode。
因此,理论与实践之间存在差距。
我们能否取消探索起始(exploring starts)的要求呢?接下来,我们将通过软策略(soft policies)来证明这一点。
五.MC 没有探索就启动(MC without exploring starts):Algorithm: MC ε-Greedy
1.算法介绍
由上面的思考,引出了第五部分,如何把?exploring starts 这个条件给去掉,这里给出了一个算法叫?MC ε-Greedy
什么是 soft policy?
- 如果采取任何动作的概率都是正数,对每一个 action 都有可能去做选择,那么该政策就是软性的。
- policy 分为两种,一种是确定性的(deterministic)policy,之前讲的 greedy policy 就是deterministic;另一种是随机性的(stochastic),这里的 soft policy 包括后面要介绍的?ε-Greedy 都是 stochastic policy
为什么要引入 soft policy?
- 如果采用软策略,如果我从一个 state-action pair 比如说 (s,a) 出发,如果后面的 episode 特别长,因为它是探索性的,我能够确保任何一个 s 和 a 都能被这个 episode 访问到。一些足够长的 episodes 就可以访问每一个状态-行动对。
- 这样,我们就不需要从每个状态-行动对开始的大量 episodes 了。因此,可以取消探索起始(exploring starts)的要求。不需要从每一个 (s,a) 都出发了,只需要从一个或者几个出发,就能够覆盖到其他的。
我们使用的是什么 soft policy?
- ε-greedy policies(除了这个还有其他软策略,当前使用的是这个而已)
什么是?ε-greedy policy?

为什么使用?ε-greedy policy?
- 平衡开发(或者叫充分利用)(exploitation)与探索(exploration)
- 充分利用 exploitation:比如我在一个状态,有很多 action,我知道里面有的 action 的 action value 比较大,那么我知道这些信息,下一时刻我就应该去采取那个 action,那么未来我相信我就能得到更多的 reward
- 探索(exploration):我现在虽然知道那个 action 能够带来更多的 reward,但是也许现在的信息不完备,我应该去探索一下其他的 action,执行完之后可能发现其他的 action 的 action value 可能也是非常好的

如何将 ε-greedy?嵌入基于 MC 的 RL 算法(基于蒙特卡洛的强化学习算法)?如何将两者结合?
最初,MC Basic 和 MC Exploring Starts 中的策略改进(policy improvement)步骤是求解下面的式子:(在第一步求解出了 q_πk (s, a),这一步要求解下面这个优化问题得到一个新的策略)
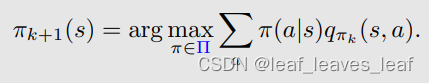
之前我们没有强调过,但其实我们在求解这个优化问题的时候,π 应该在所有可能的策略当中去做选择,其中,Π 表示所有可能策略组成的集合。这里求解出的最优策略是:
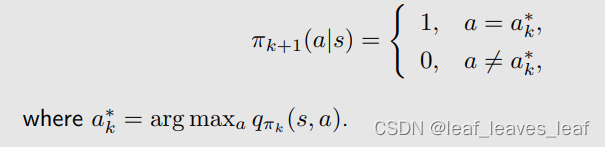
上面的是我们之前的方法,现在要把?ε-greedy?嵌入基于 MC 的 RL 算法:
现在,策略改进(policy improvement)步骤改为求解

在求解上面这个问题的时候,我不是在所有的策略里面去找,只是在 Πε 里面去找。其中,Πε 表示具有固定 ε 值的所有 ε-greedy 策略的集合(这里?ε 是事先给定的)。
这时候所得到的最优策略是:(把最大的概率仍然给 greedy action,但是会给其他所有 action 都给一个相同的比较小的概率)
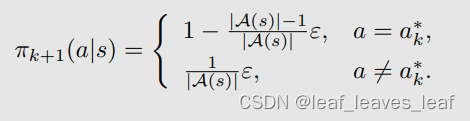
- 这样我们就得到了 MC?ε-greedy 的算法,MC ε-Greedy 与 MC Exploring Starts 相同,只是前者使用 ε-greedy 策略,后者使用 greedy 策略。
- 它不需要探索起点(exploring starts)这样的一个条件,但仍需要以不同的形式访问所有的状态-动作对。It does not require exploring starts, but still requires to visit all state-action pairs in a different form.
伪代码:

2.例子
(1)讨论? ε-greedy 的探索性:
一个 episode 能访问所有状态-行动对吗?Can a single episode visit all state-action pairs?
当 ε = 1 时,策略是均匀分布(uniform distribution)的,在我们的例子里面每一个状态有 5 个 action,每一个 action 都给了 0.2 的概率(由上面那个图片的最后一个公式可以计算出来)。当 ε = 1 时,探索能力(exploration ability)最强。
看图 (a),从一点出发,根据策略要生成一个 episode,如果只有 100 步的话,图 (a) 是它探索的情况,探索到了不少的 state;如果有1000步,图 (b) 可知,所有的 state 和 action 都被探索到了;如果有10000步,探索的次数会更大;图 (d) 是探索100万步的时候,每一个 state-action pair 被访问的次数,横轴代表 state-action pair 的索引,共有25个状态,每个状态有 5 个 action,所以一共有 125 个 state-action pair,这时候虽然只有一个 episode,但是每个 state-action pair 都被访问了很多次。

这个例子说明了,当?ε 比较大的时候,探索性比较强,自然就不再需要用 exploring starts 这样的一个条件了,不需要从每一个 (s,a) 出发都有一个 episode,只需要从某一些 (s,a) 出发,我就能覆盖到其它所有的 (s,a)。
当 ε 较小时,策略的探索能力(exploration ability)也较小。

图 (a),步数比较小的时候,访问的 state 比较少,因为它的偏好比较强;即使我把 episode 的长度变成了 100 万步,他会呈现出非常不均匀的访问次数,有的 state value 被访问的次数多,有的少。不管怎么样,相比 greedy 来说,还是有一定的探索能力。
下面用 MC ε-Greedy 算法实验一个例子:
运行 MC ε-Greedy 算法如下。在每次迭代中(In every iteration),执行下面的:
- 在 episode 生成步骤中,使用先前的 ε-Greedy 策略生成一个 episode,这个 episode 非常长,有一百万步!
- 在其余步骤中,使用这一个 episode 更新所有的 state-action pair 它们相对应的 action value 和更新策略。
- 之所以这样做,是想通过这个例子展示一下这个算法避开了 exploring starts 这样的一个条件,因为只要这个 episode 足够长,即使它从一个 state-action pair 出发,但仍然能够访问其他所有的?state-action pair。
- 两次迭代可以得到最优的 ε-Greedy 策略
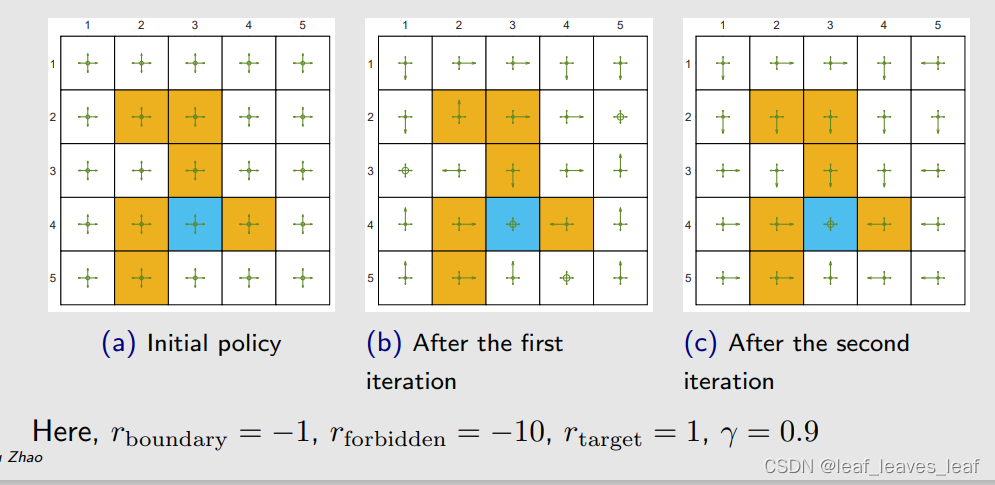
- 图 (a) 是最初的策略,这个策略是不好的,在每一个状态都有相同的概率去选择所有的 action。然后我用这样一个策略生成一个 100 万步长的 episode,然后更新策略,得到了图 (b) 这样的策略;这个策略仍然不够好,一些状态上会保持不动;然后再用这个策略得到一个 100 万步长的 episode,再去更新策略,就得到了图 (c) 这样的策略。
- 我们看图 (c) 这样的策略,如果只看图上绿色箭头概率最大的 action(箭头最长的方向),比图 (b) 策略来说相对而言比较合理,从任何一点出发都能到达目标,但是它们会穿过障碍物,所以从这个意义上讲它还不是最优的,因为最优的应该绕过障碍物到达目标。所以 ε-Greedy 通过探索性得到了一些好处,但是牺牲掉了最优性。
与贪婪策略(greedy policy)相比
- ε-greedy 策略的优势在于它们具有更强的探索能力,因此不需要探索开始(exploring starts)的条件。
- 缺点是 ε-greedy 策略一般来说不是最优的(not optimal)(我们只能证明总是存在最优的 greedy 策略)。
- 实际中可以设置应该比较小的?ε 值,当这个?ε 趋于 0 的时候,ε-greedy 就接近于 greedy,所以用这个算法找到的最优的? ε-greedy 策略就接近于最优的? greedy 策略;在实际中也可以让?ε 逐渐减小,比如在开始的时候??ε 比较大,就有比较强的探索能力,然后让??ε 逐渐趋于 0,最后得到的策略又又比较好的最优性。
- MC ε-greedy 算法给出的最终策略只有在所有 ε-greedy 策略的集合 Πε 中才是最优的。
- ε不能太大。
下面我们用几个例子说明一下 ε-greedy 的最优性

在下面的例子中,首先给出左图绿色箭头的一个策略,然后求解它的贝尔曼公式,可以得到它的 state value(右图)。

- 左上角第一幅图的 ε = 0,它是一个 greedy 的策略,并且它是在这个情况下最优的一个策略。
- 右上角的第二幅图 ε = 0.1,是第二个策略,第二个策略与第一个策略的关系是,他们是一致的(consistent),因为左下角那个小格子上,第一幅图中是往上走,第二幅图中最大的概率(最长的绿色箭头)是往上走,但与从同时也给其他的 action 有一些比较小的概率(小箭头),这个就被称为 consistent,这时候使用左图策略算出的 state value 比第一幅图的小,就是因为在很多地方它采取了不该采取的措施。
- consistent:右上角的第二幅图 ε = 0.1,是第二个策略,第二个策略与第一个策略的关系是,他们是一致的(consistent),因为在第二幅图的左图中的任意一个状态中,箭头最长的策略(具有最大概率的策略)和第一幅图左图的策略一样。
- 进一步增大?ε,state value 变得更小,我们知道?state value 可以用来衡量一个策略是否好,最优策略的定义就是基于?state value,最优策略是有最大的?state value
- 因此虽然所有策略都和最优的 greedy 策略保持一致(绿色箭头一样),但最优性变得越来越差
- 实际上 target area 上的 state value 在最优的策略里,应该是最大的值,但当?ε 比较大的时候,它反而变成最小的值,变成负数,因为它在这个地方有比较大的概率进入 forbidden area,得到很多对负数 reward。
下面例子说明 MC ε-Greedy 算法中?ε 的选择不能太大。或者最开始的时候?ε 比较大,探索性比较强,最后?ε 逐渐减小到 0,就可以得到一个最优的策略

- 左上角第一幅图的 ε = 0,它是一个 greedy 的策略,并且它是在这个情况下最优的一个策略。
- 用 MC ε-Greedy 得到的 optimal?ε-Greedy 策略,得到这个策略之后要用到实际中,实际中不会带有?ε(即右上角的左图不会有小箭头了,只保留概率最大的策略,即只保留大箭头),会把它转成对应的 greedy 策略,这个转换成的 greedy 策略,我希望它与最优策略(左上角的左图策略)相同,即我们希望是具有一致性的(consistent)。在?ε=0.1 的时候,把它转成 greedy 的时候与左上角左图相同,就是 greedy 的策略。但当?ε=0.2 或更大的时候,ε-Greedy 策略与左上角的 greedy 策略无关了,转换过去(即只取最长的箭头,不要小箭头)他俩就不同了
- 因此?ε 的选择不能太大
?六.总结

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Systemctl | 系统服务管理利器
- Python为何那么流行?Python火的资本在哪里?
- Linux 内存优化性能实战
- ES6(ECMAScript 6.0)
- 算法基础之快速幂
- 探秘 Python 协程:解锁异步编程的超能力
- 爬山算法优化遗传算法优化极限学习机的多分类预测,p-ga-elm多分类预测
- 仓库管理软件有哪些比较好用?
- 【法如faro】法如三维激光扫描软件Scene2023下载与安装教程
- 【INTEL(ALTERA)】错误 (19021):相同的文件名 xx 用于不同的 IP 文件。同一个名称不能用于多个 IP 文件。