机器学习模型可解释性的结果分析
????????模型的可解释性是机器学习领域的一个重要分支,随着 AI 应用范围的不断扩大,人们越来越不满足于模型的黑盒特性,与此同时,金融、自动驾驶等领域的法律法规也对模型的可解释性提出了更高的要求,在可解释 AI?一文中我们已经了解到模型可解释性发展的相关背景以及目前较为成熟的技术方法,本文通过一个具体实例来了解下在 MATLAB 中是如何使用这些方法的,以及在得到解释的数据之后我们该如何理解分析结果。
要分析的机器学习模型
我们以一个经典的人体姿态识别为例,该模型的目标是通过训练来从传感器数据中检测人体活动。传感器数据包括三轴加速计和三轴陀螺仪共6组数据,我们可以通过手机或其他设备收集,训练的目的是识别出人体目前是走路、站立、坐、躺等六种姿态中的哪一种。我们将收集到的数据做进一步统计分析,如求均值和标准差等,最终获得18组数据,即18个特征。然后可以在 MATLAB 中使用分类学习器 App 或者通过编程的形式进行训练,训练得到的模型混淆矩阵如下,可以看到对于某些姿态的识别,模型会存在一定误差。那么接下来我们就通过一系列模型可解释性的方法去尝试解读一下错误判别的来源。
从混淆矩阵中可以看到,模型对于躺 ‘Laying’ 的姿态识别率为 100%,而对于正常走路和上下楼这三种 ‘Walking’ 的姿态识别准确率较低,尤其是上楼和下楼均低于70%。这也符合我们的预期,因为躺的姿态和其他差别较大,而几种走路之间差异较小。
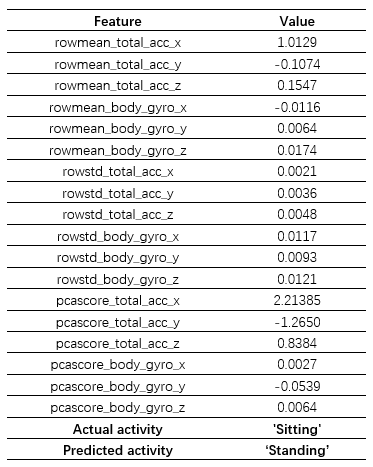
但我们也留意到模型在 ‘Sitting’ 和 ‘Standing’ 之间也产生了较大的误差,考虑到这两者之间的差异,我们想探究一下产生这种分类错误背后的原因。首先我们从图中所示的区域选择了一个样本点 query point,该样本的正确姿态为 ‘Sitting’,但是模型识别成了 ‘Standing’,为便于下一步分析,这里将该样本点所有特征及其取值列举了出来,如前所述一共 18 个,分别对应于原始的6个传感器数据的平均值、标准差以及第一主成分:
使用可解释性方法进行分析
模型可解释性分析的目的在于尝试对机器学习黑盒模型的预测结果给出一个合理的解释,定性地反映出输入数据的各个特征和预测结果之间的关系。对于预测正确的结果,我们可以判断预测过程是否符合我们基于领域知识对该问题的理解,是否有一些偶然因素导致结果碰巧正确,从而保证了模型可以在大规模生产环境下做进一步应用,也可以满足一些法规的要求。
而对于错误的结果,如上文中的姿态识别,我们可以通过可解释性来分析错误结果是由哪些因素导致的,更具体地说,即上述 18 个特征对结果的影响。在此基础上,可以更有针对性地进行特征选择、参数优化等模型改进工作。
接下来我们就尝试用几种不同的可解释性方法来对上文中的 query point 做进一步分析,希望可以找到一些模型分类错误的线索。
2.1 Shapley 值
我们尝试的第一个方法是 Shapley 值,Shapley 值起源于合作博弈理论,它基于严格的理论分析并给出了完整的解释。作为一个局部解释方法,Shapley 值通过对所有可能的特征组合依次计算,从而得到每个特征对预测结果的平均边际贡献,并且这些值是相对于该分类的平均得分而言的。可以简单理解为边际贡献的分值越高,对产生当前预测结果的影响越大。因为有着完善的理论基础且发展时间较长,Shapley 值被广泛应用于金融领域来满足一些法律法规的要求。
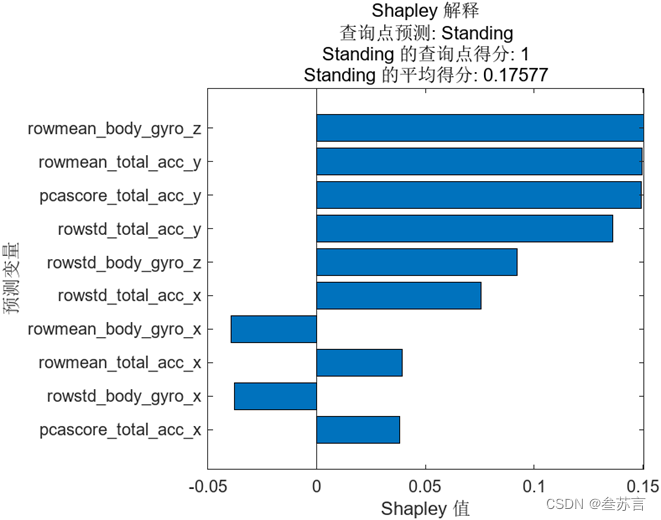
我们之前已经了解到 Shapley 值反应的是每个特征的平均边际贡献,并且这些值是相对于该分类的平均得分而言的。首先需要计算出 ‘Standing’ 的平均得分,我们会将数据集中所有点关于 ‘Standing’ 的预测得分取平均得到相应的值,即 0.17577。而我们关注的样本点预测为 ‘Standing’ 的得分为 1,相对较高,它和所有点的平均值相比差值为 0.82423,Shapley 值反应的正是该样本点中每个特征对这个差值的贡献,其总和也正是 0.82423。
图中显示了排行前十的特征及对应的 Shapley 值,我们可以看到 rowmean_body_gyro_z 的值最大,说明它对错误判别的影响最大,当然紧随其后的几个特征的 Shapley 值也较为接近。
特征 rowmean_body_gyro_z的实际含义为z方向陀螺仪的平均值,为什么这个特征可能导致了错误的结果?我们可以接着往下分析。
2.2 PDP - Partial Dependency Plot
Shapley 值虽然很清晰地给出了各个特征对于最终预测结果的贡献,但是我们需要更多的信息来分析错误产生的来源,一个有效的方法是结合 PDP 又称部分依赖图来进行查看。
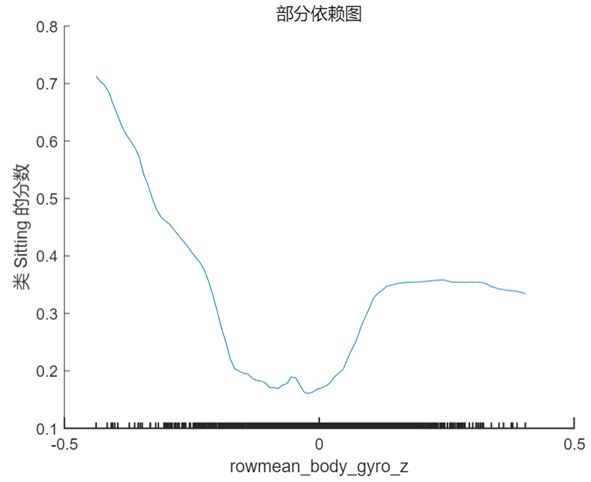
PDP 是一个全局解释方法,关注单个特征对某一预测结果的整体影响,其思想是假设所有样本中的该特征等于某一个固定值,从而计算出一个预测结果的平均值。当我们将该特征取一系列值时(取值范围仍然来源于样本),便可以绘制出对应的曲线。我们接着 Shapley 值的分析选择特征 rowmean_body_gyro_z(对应数据中的位置为第6个特征),以及 query point 对应的真实分类 ‘Sitting’ 和错误分类 ‘Standing’ 分别绘制 PDP,在 MATLAB 中使用的方法仍然非常简单,具体代码及对应结果如下:
plotPartialDependence(model,6,'Sitting');
% rowmean_body_gyro_z is the 6th predictor in our data table
plotPartialDependence(model,6,'Standing');
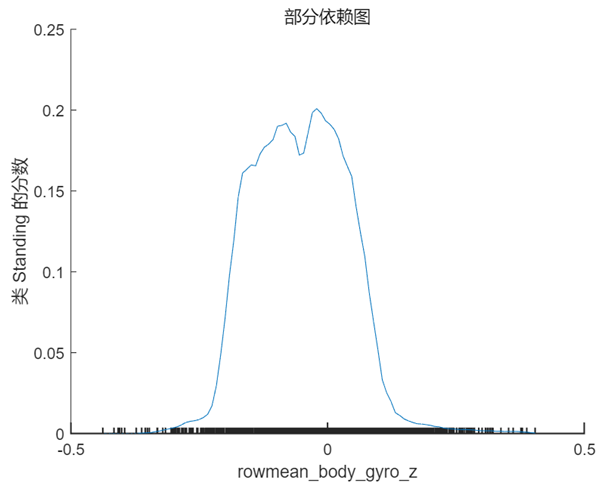
根据上图以及第 1 节中 query point 在该特征的实际取值 0.017 可以看出,当该特征的取值接近于 0 时,分类为 ‘Standing’ 的分数较高,而当取值向两端靠拢尤其是接近于 -0.5 时分类为 ‘sitting’ 的分数较高,甚至大于 0.5,这也符合该点的实际预测值。
通过部分依赖图我们对 Shapley 值的分析结果有了更清楚的认识,虽然该样本点的预测结果是错误的,但结合原始数据可以看出,这样的结果是有迹可循且合理的。
??????????免费分享一些我整理的人工智能学习资料给大家,整理了很久,非常全面。包括一些人工智能基础入门视频+AI常用框架实战视频、图像识别、OpenCV、NLP、YOLO、机器学习、pytorch、计算机视觉、深度学习与神经网络等视频、课件源码、国内外知名精华资源、AI热门论文等。
下面是部分截图,加我免费领取
目录
一、人工智能免费视频课程和项目
二、人工智能必读书籍
最后,我想说的是,自学人工智能并不是一件难事。只要我们有一个正确的学习方法和学习态度,并且坚持不懈地学习下去,就一定能够掌握这个领域的知识和技术。让我们一起抓住机遇,迎接未来!
上面这份完整版的Python全套学习资料已经上传至CSDN官方,朋友如果需要可以点击链接领取?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!