代码训练营Day.20 | 654. 最大二叉树， 617. 合并二叉树，700. 二叉搜索树中的搜索，98. 验证二叉搜索树

654. 最大二叉树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

3. 解法

与知道中序和后序数列的情况下啊构造树一样，将左右区间标出更省空间。

class Solution {
public:
    int maxe(vector<int>& nums, int left, int right) {
        int max = left;
        for (int i = left; i < right; i++) {
            if (nums[i] > nums[max]) max = i;
        }
        return max;
    }
    TreeNode* construct(vector<int>& nums, int left, int right) {
        if (left >= right) return NULL;
        int max = maxe(nums, left, right);
        TreeNode* root = new TreeNode(nums[max]);
        root->left = construct(nums, left, max);
        root->right = construct(nums, max + 1, right);
        return root;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return construct(nums, 0, nums.size());
    }
};

不太省的

class Solution {
public:
    int maxe(vector<int>& nums) {
        int max = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] > nums[max]) max = i;
        }
        return max;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if (nums.empty()) return NULL;
        int max = maxe(nums);
        TreeNode* root = new TreeNode(nums[max]);
        vector<int> left(nums.begin(), nums.begin() + max);
        vector<int> right(nums.end() - nums.size() + max + 1, nums.end());
        root->left = constructMaximumBinaryTree(left);
        root->right = constructMaximumBinaryTree(right);
        return root;
    }
};

617. 合并二叉树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

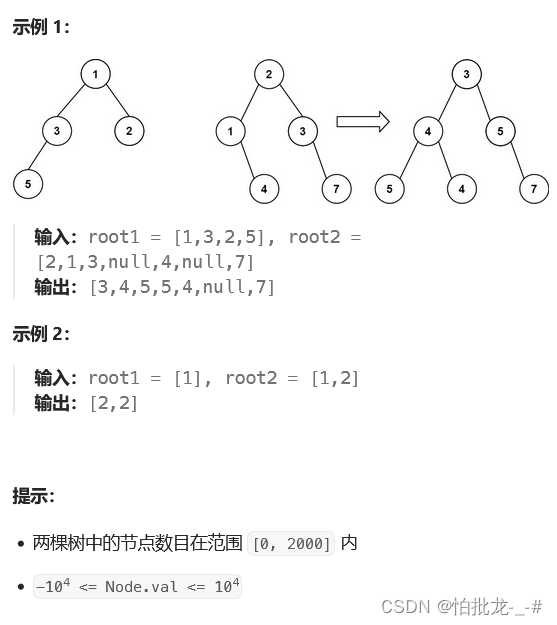
3. 解法

递归，如代码所示。让root1最终承载最后的树。

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL) return root2;
        if (root2 == NULL) return root1;
        root1->val += root2->val;
        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);
        return root1;
    }
};

迭代法，与判断二叉树是否对称相似，两个两个走，注意，先判断是否两个都不是NULL而可以push，再考虑root1子树是NULL的情况而替换成root2子树。for循环注意stride。

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL) return root2;
        if (root2 == NULL) return root1;
        queue<TreeNode*> qu;
        qu.push(root1);
        qu.push(root2);
        while (!qu.empty()) {
            int size = qu.size();
            for (int i = 0; i < size; i+=2) {
                TreeNode* cur1 = qu.front();
                qu.pop();
                TreeNode* cur2 = qu.front();
                qu.pop();
                cur1->val += cur2->val;
                if (cur1->left != NULL && cur2->left != NULL) {
                    qu.push(cur1->left);
                    qu.push(cur2->left);
                }
                if (cur1->right != NULL && cur2->right != NULL) {
                    qu.push(cur1->right);
                    qu.push(cur2->right);
                }
                if (cur1->left == NULL) cur1->left = cur2->left;
                if (cur1->right == NULL) cur1->right = cur2->right;
            }
        }
        return root1;    
    }
};

700. 二叉搜索树中的搜索

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

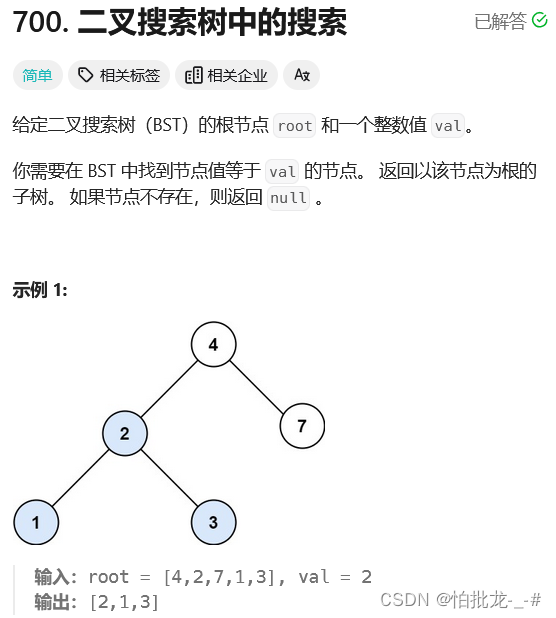
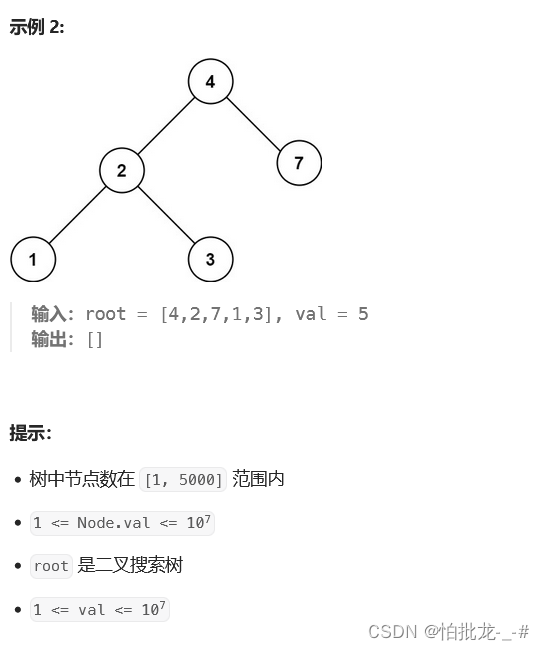
3. 解法

1. 普通树

迭代，普普通通遍历。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        queue<TreeNode*> qu;
        qu.push(root);
        while (!qu.empty()) {
            int size = qu.size();
            for (int i = 0; i < size; i++) {
                TreeNode* cur = qu.front();
                qu.pop();
                if (cur->val == val) return cur;
                if (cur->left) qu.push(cur->left);
                if (cur->right) qu.push(cur->right);
            }
        }
        return NULL;
    }
};

递归，在判断root->val之前，一定要确保root != NULL。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL) return NULL;
        if (root->val == val) return root;
        TreeNode* left = searchBST(root->left, val);
        TreeNode* right = searchBST(root->right, val);
        if (left != NULL && left->val == val) return left;
        if (right != NULL && right->val == val) return right;
        return NULL;
    }
};

2. 二叉搜索树

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

递归：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL) return NULL;
        if (root->val == val) return root;
        else if (root->val < val) return searchBST(root->right, val);
        else return searchBST(root->left, val);
    }
};

迭代：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        queue<TreeNode*> qu;
        qu.push(root);
        while (!qu.empty()) {
            int size = qu.size();
            for (int i = 0; i < size; i++) {
                TreeNode* cur = qu.front();
                qu.pop();
                if (cur->val == val) return cur;
                else if (cur->val > val && cur->left != NULL) qu.push(cur->left);
                else if (cur->val < val && cur->right != NULL) qu.push(cur->right);
            }
        }
        return NULL;
    }
};

98. 验证二叉搜索树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

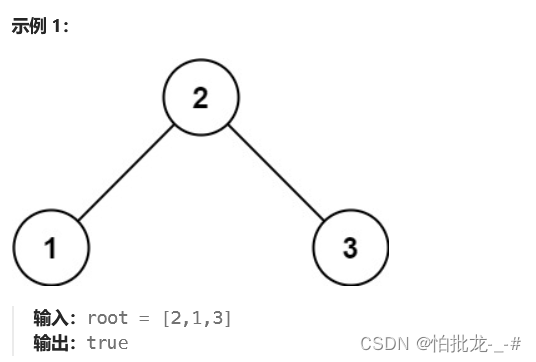
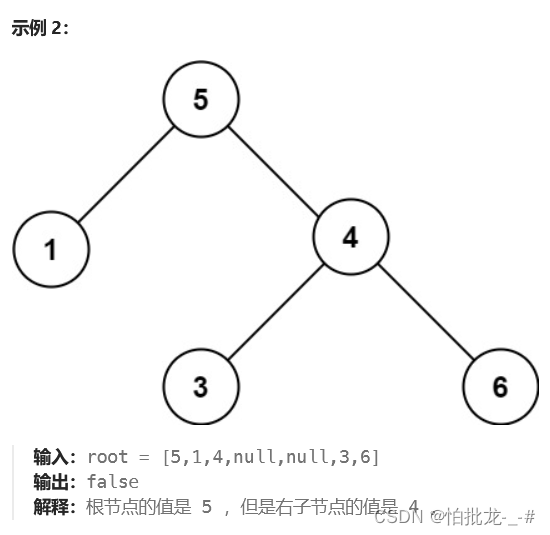
3. 解法

1）递归，一棵树是否为有效二叉搜索树，取决于两个条件：1. 两棵子树都是二叉搜索树；2. 左子树的最大值小于root->val，右子树的最小值大于root->val。

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        while (left != NULL && left->right != NULL) left = left->right;
        if (left != NULL && left->val >= root->val) return false;
        while (right != NULL && right->left != NULL) right = right->left;
        if (right != NULL && right->val <= root->val) return false;
        return isValidBST(root->left) && isValidBST(root->right);
    }
};

2）中序遍历后的数组是否单调递增！可以构造数组，也有不构造数组的方法。记录最大值或者上一个结点，及在中序递归时，如果是二叉搜索树，下一个要遍历的结点值必大于当前值。否则就不是二叉搜索树。

## 记录最大值。
class Solution {
public:
    long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;

        bool left = isValidBST(root->left);
        // 中序遍历，验证遍历的元素是不是从小到大
        if (maxVal < root->val) maxVal = root->val;
        else return false;
        bool right = isValidBST(root->right);

        return left && right;
    }
};

?

## 记录结点。
class Solution {
public:
    TreeNode* pre = NULL; // 用来记录前一个节点
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        bool left = isValidBST(root->left);

        if (pre != NULL && pre->val >= root->val) return false;
        pre = root; // 记录前一个节点

        bool right = isValidBST(root->right);
        return left && right;
    }
};