数据结构与算法之树与森林的遍历

1 树的遍历

1.1 树的逻辑结构

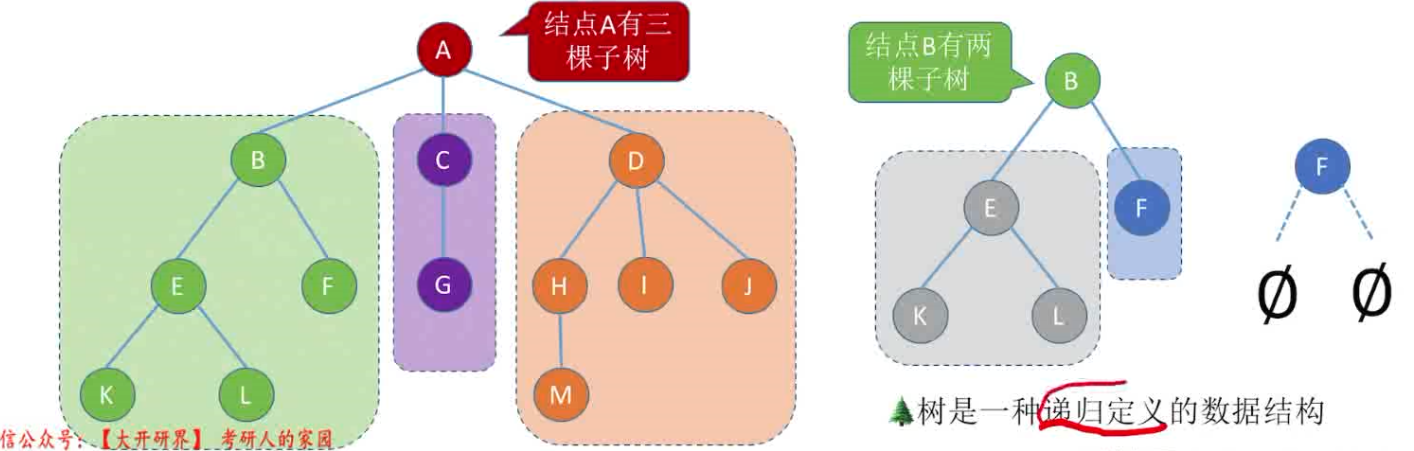
树是n(n≥0)个结点的有效集合，n=0时，称为空树，这是一种特殊情况。在任意一颗非空树中应该满足：

1. 有且仅有一个特定的称为根的结点
2. 当n＞1时，其余节点可分为m(m>0)个互不相交的有限集合 $T_1,T_2....T_n$ 其中每个集合本身也是一颗树，并且称为根节点的子树。

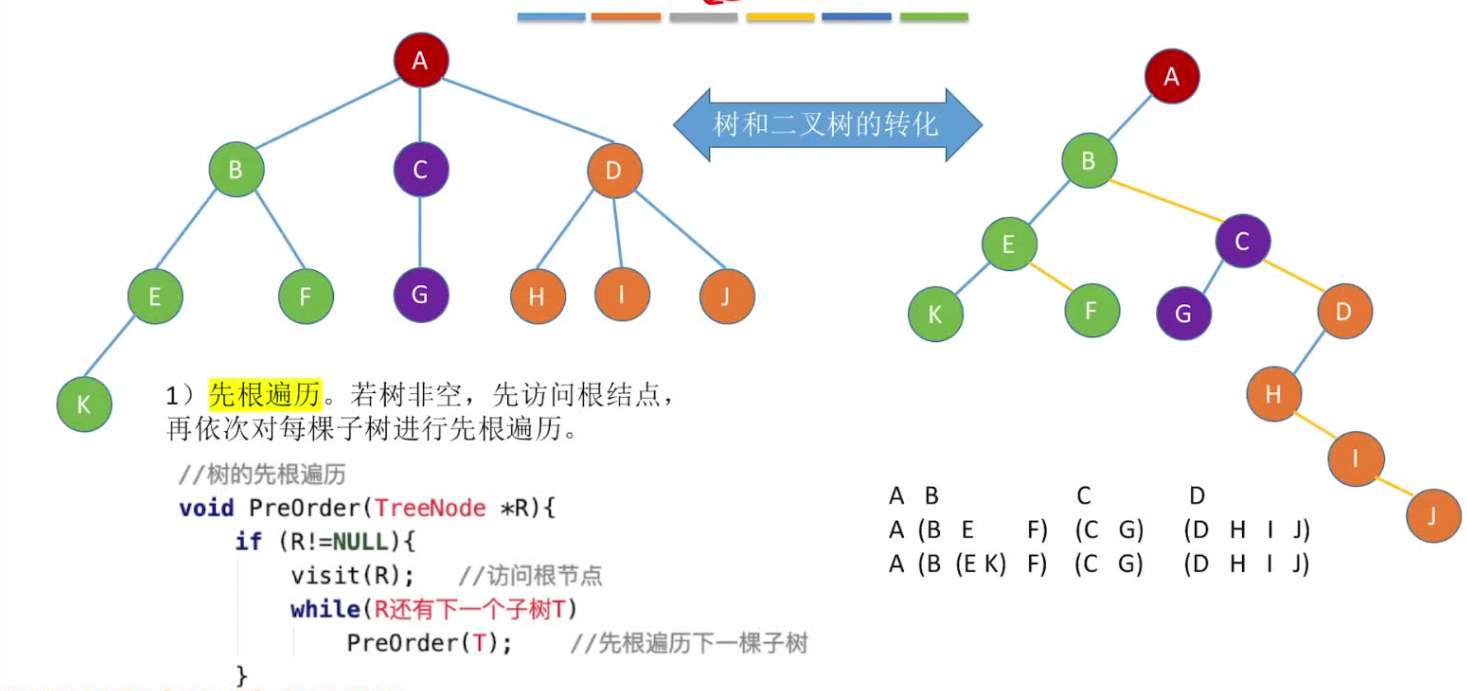
1.1.1 树的先根遍历

1. 先根遍历：若树非空，先访问根节点，在依次对每颗子树进行先根遍历。

void preOrder(TreeNode *R){
	if(R!=NULL){
		visit(R);//访问根节点
		while(R还有下一个子树T){
			preOrder(T);//先根遍历下一颗子树
		}
	}
}

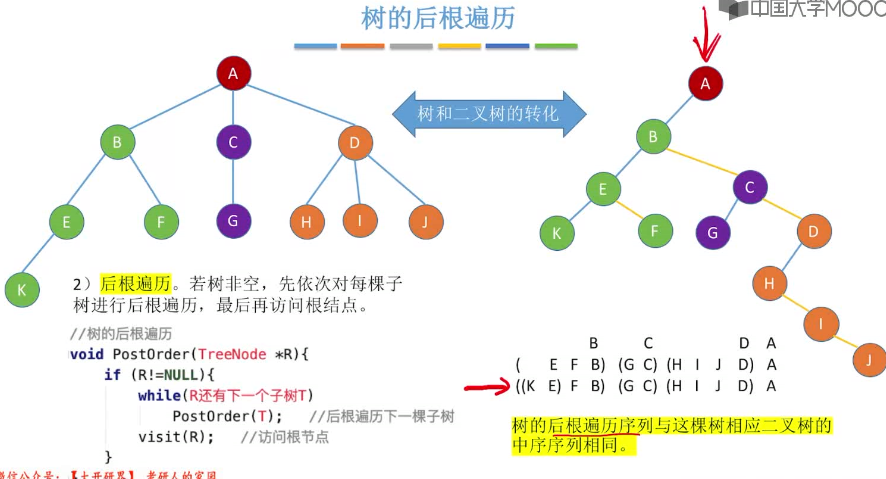
1.1.2 树的后根遍历

1. 后根遍历：若树为空，先依次对每颗子树进行后根遍历，最后在访问根节点。

void postOrder(TreeNode *R){
	if(R!=NULL){
		while(R还有下一个子树T){
			preOrder(T);//先根遍历下一颗子树
		}
	visit(R);//访问根节点
	}
}

1.1.3 树的层次遍历

1. 层次遍历(用队列实现)
   1. 若树非空，则根节点入队
   2. 若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队
   3. 重复2直到队列为空

5.6 二叉树的层序遍历

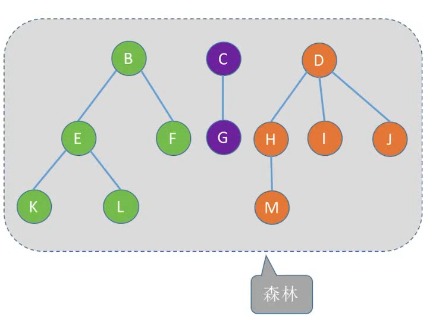
2 森林的逻辑结构

森林。是m(m≥0)棵互不相干的树的集合。每棵树去掉根节点后，其各个子树又组成森林

2.1 森林的先序遍历

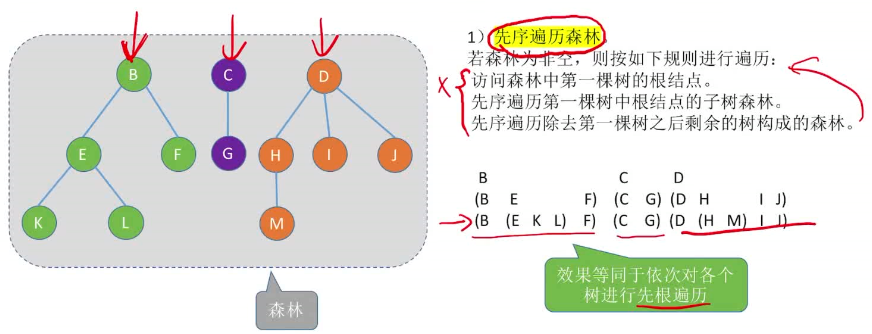
先序遍历森林：若森林为非空，则按如下规则进行遍历：

1. 访问森林中第一棵树的根节点。
2. 先序遍历第一棵树中根节点的子树森林，
3. 先序遍历除去第一棵树之后剩余的树构成的森林。

效果等同于依次对各个树进行先根遍历

2.2 森林的中序遍历

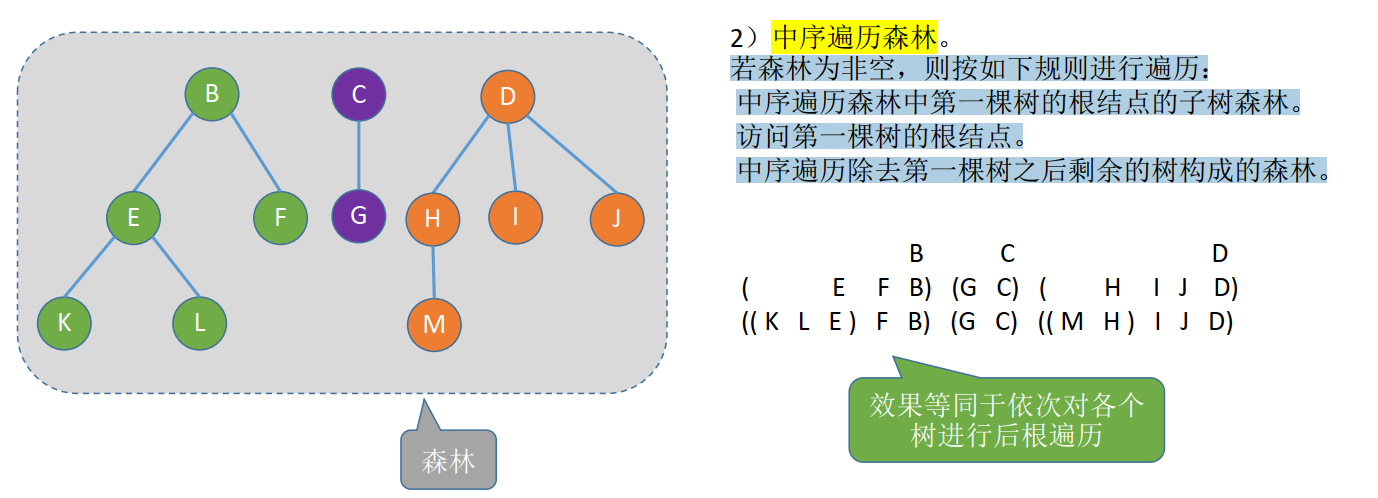
若森林为非空，则按如下规则进行遍历：

1. 中序遍历森林中第一棵树的根结点的子树森林。
2. 访问第一棵树的根结点。
3. 中序遍历除去第一棵树之后剩余的树构成的森林。

效果等同于依次对各个树进行后根遍历