面试算法112：最长递增路径

题目

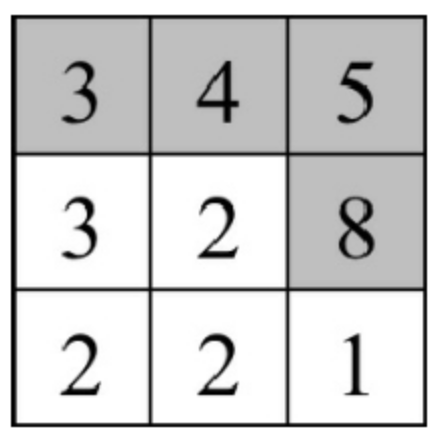
输入一个整数矩阵，请求最长递增路径的长度。矩阵中的路径沿着上、下、左、右4个方向前行。例如，图中矩阵的最长递增路径的长度为4，其中一条最长的递增路径为3→4→5→8，如阴影部分所示。

分析

由于需要搜索图中的所有节点才能确定最长递增路径的长度，因此这也是一个关于图搜索的问题。解决图搜索通常用广度优先搜索和深度优先搜索这两种不同的方法。这个问题中的路径是非常关键的信息，而深度优先搜索能够很方便地记录搜索的路径，因此深度优先搜索更适合这个问题。
因为不知道从哪个节点开始的递增路径是最长的，所以试着找出从矩阵的每个数字出发的最长递增路径的长度，通过比较可以得出整个矩阵中的最长递增路径的长度。

解

public class Test {
    public static void main(String[] args) {
        int[][] matrix = {{3, 4, 5}, {3, 2, 8}, {2, 2, 1}};
        int result = longestIncreasingPath(matrix);
        System.out.println(result);
    }

    public static int longestIncreasingPath(int[][] matrix) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        if (rows == 0 || cols == 0) {
            return 0;
        }

        int[][] lengths = new int[rows][cols];
        int longest = 0;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                int length = dfs(matrix, lengths, i, j);

                longest = Math.max(longest, length);
            }
        }

        return longest;
    }

    private static int dfs(int[][] matrix, int[][] lengths, int i, int j) {
        if (lengths[i][j] != 0) {
            return lengths[i][j];
        }

        int rows = matrix.length;
        int cols = matrix[0].length;
        int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int length = 1;
        for (int[] dir : dirs) {
            int r = i + dir[0];
            int c = j + dir[1];
            if (r >= 0 && r < rows && c >= 0 && c < cols && matrix[r][c] > matrix[i][j]) {
                int path = dfs(matrix, lengths, r, c);
                length = Math.max(path + 1, length);
            }
        }

        lengths[i][j] = length;
        return length;
    }

}