主成分分析法
发布时间:2024年01月08日
主成分分析法
PCA
综述:数据降维的方法
可以用一种线性变换的思想去理解,比如二维的一条直线,我们可以通过变换,使得这一条直线落在x或y轴上,达到降维的效果。
如图:二维一条直线
主成分分析法
PCA
综述:数据降维的方法
可以用一种线性变换的思想去理解,比如二维的一条直线,我们可以通过变换,使得这一条直线落在x或y轴上,达到降维的效果。
如图:二维一条直线
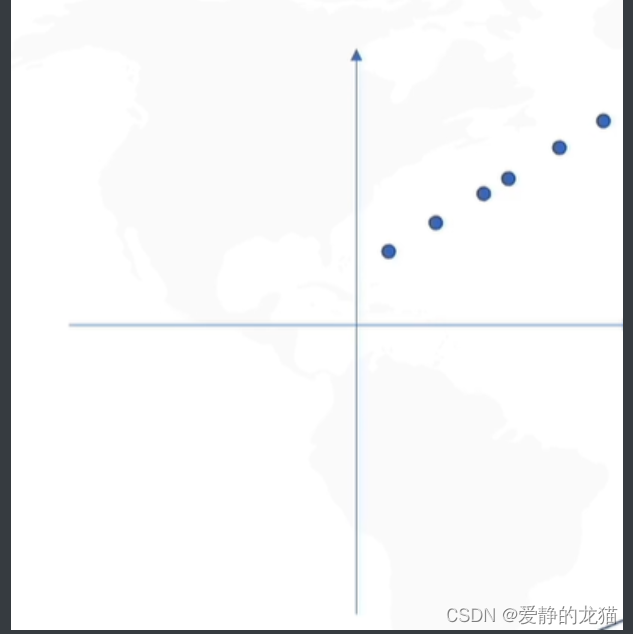
如图:变换坐标系
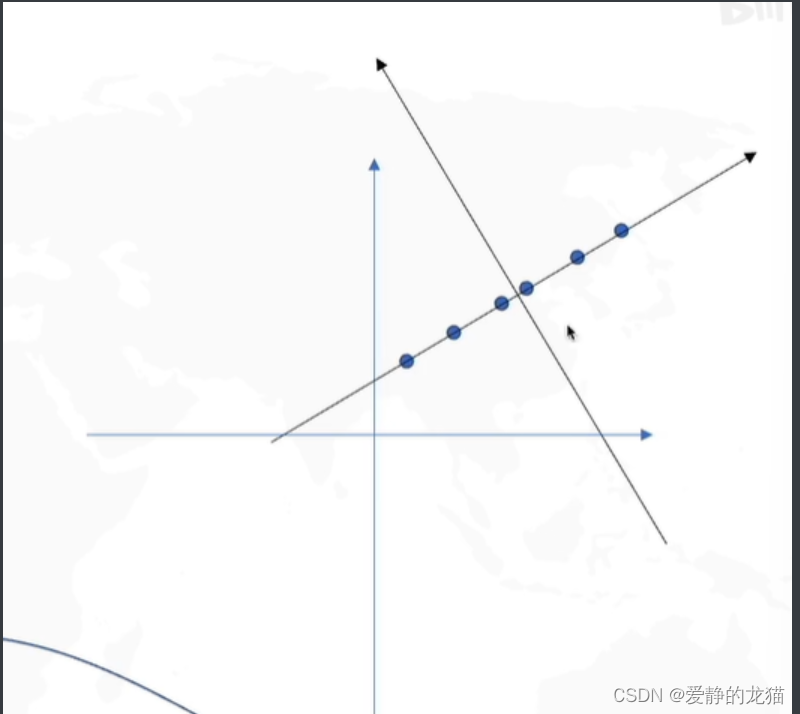
这时候就可以重新定义一下 PCA 的目标:在只保留一个轴时候,使得信息保留最多(二维)
部分知识:
去中心化(把坐标原点放在数据中心)
找坐标系,找到数据方差最大的方向,就是第一主成分。(如果第一主成分不足以表达,就考虑吧选取第二个)
为了有效反映原来信息,第一主成分和第二主成分的协方差为0.以此类推可以获得p个主成分。这些主成分是互不相关,是依次递减的。
累计方差贡献率大于百分之80就可以了,或者特征根大于1就可以了。
?根据线性代数的知识,我们需要一则伸缩,二则旋转,伸缩不是问题
旋转的矩阵R又从何而来?
即是协方差矩阵的特征向量就是R。
协方差定义=
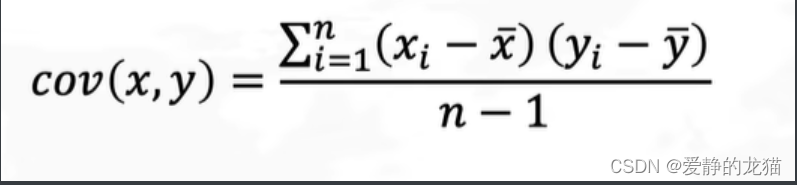
上面是没有经过中心化的协方差公式
下面经过中心化之后,均值已经变成0了,所以的得到公式
=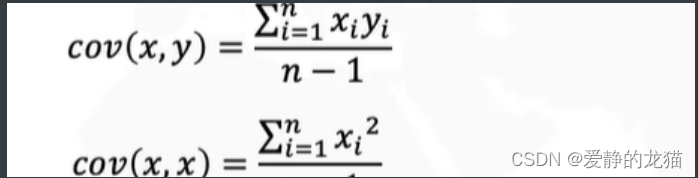

协方差表示的是两个变量在变化过程中是否同方向变化,还是反方向变化,同向或者反向的程度如何呢?
(二维)

计算步骤
1.假设样本有n个样本,p个指标,可以构成n*p的样本矩阵x

2.标准化处理,计算均值和标准差,进行标准化
3.将上述矩阵进行协方差的计算
求出矩阵R

以上两步可以合成1步
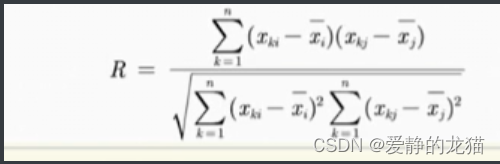
4.借由矩阵R,求出特征值和特征向量(R是半正定矩阵,tr(R)=p)
求出特征向量(以上可以由编程工具计算得出)
5.计算主成分贡献率和累计贡献率。取前百分之八十就可以了

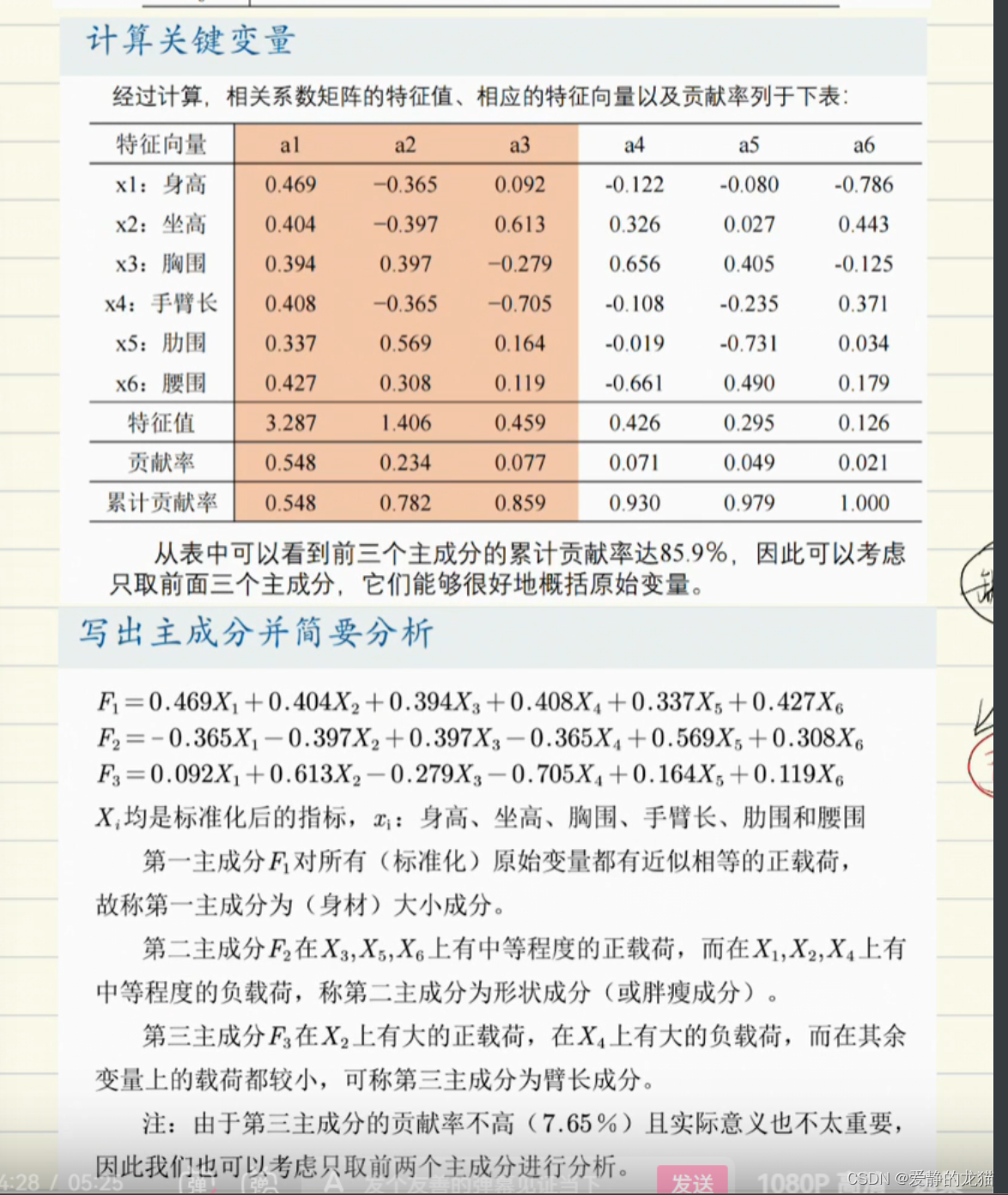
小样例示范
文章来源:https://blog.csdn.net/2302_79394843/article/details/135438318
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 认证评价的方法
- 网站安全每日话题——网页内容被篡改怎么办
- 前瞻性解析:数字孪生技术真正的实用价值
- 低代码助力制造业数智转型,激发创新力迎接工业 4.0
- docker——docker compose简介和案例(部署prometheus+granfana+node-exporter)
- YOLOv8改进 | 损失篇 | VarifocalLoss密集目标检测专用损失函数 (VFLoss,原论文一比一复现)
- 小知识分享3
- 国科大机器学习期末复习题库
- 万众瞩目!酷开科技揽获多项大奖!
- vue3+echart绘制中国地图并根据后端返回的坐标实现涟漪动画效果