初识计算机图形学

初识计算机图形学

笔记来源：【老奇】阴差阳错 撼动世界的游戏引擎

1.MVP Transformation

详见本人博客：
1.Transformation
2.梳理从MVP变换到光栅化的过程
MVP变换将空间中3D物体投影到2D屏幕

2.Rasterization

详见本人博客：
1.Rasterization（光栅化）
2.梳理从MVP变换到光栅化的过程

场景是一个个由三角面组成的模型

将模型投射到像素就得到一张图像，这就是渲染

将模型投射到像素，投射过程从左到右，从上到下，一行行如窗户栅栏，这种渲染方式叫光栅化渲染

3.Shading

物体的材质（material）以及光照的角度决定了shading的差异

Gouraud 插值能让棱角突出的模型（如上图）看起来光滑流畅（如下图）

4.Texture

Texture（纹理）Mapping：让模型具备现实的纹理

5.Material

画面如何才能更逼真？
渲染是光的艺术，画面假是光出现了问题
起初光没有单位，只能用强度度量，被材质反射后会衰减，具体衰减多少由材质本身决定

5.1 Lambert Material

5.2 Phong Material

5.3 Blinn-Phong Material

以上这三个模型只是经验模型，无法真实模拟现实

6.Global illumination（GI）

想要生成逼真图像，必须模拟光在场景中传播时的物理行为，而光的强度和分布，又由能量的传输和守恒原理决定，由此开始瞄准辐射度量学

6.1 BRDF（双向反射分布函数）

渲染方程和材质模型的区别：渲染方程是基于真实物理情况推导得出的
渲染方程的计算结果是否准确，也就是反射光是否准确只取决于两点：

1. 物体的BRDF（光线反弹后衰减了多少）
2. 入射光

BRDF可以看作各种材质的量化统一，Lambert模型和Phong模型就被纳入其中

Physcial-based Models（PBR 模型）

PBR模型的BRDF（光线反弹后衰减了多少）要么实验测算，要么经验统计，要么套用真实存在的物理公式，如菲涅尔反射、次表面散射

菲涅尔反射

菲涅尔反射可以模拟湖水在不同角度的折射和反射效果

次表面散射（Subsurface scattering 俗称SSS材质）

次表面散射可以表现皮肤、蜡烛等物体在背光时的半透效果

6.2 Incident light（入射光）

反射光是否真实的关键除了上述的BRDF，还有入射光。那么入射光如何确定？

场景复杂时，入射光从四面八方向物体反弹光线

也就是半球空间的所有方向都应该有入射光打过来，用对方向角度的积分表示

从场景其他地方反弹过来的光如何确定？
任取一条入射光，会发现它也由上一个反射点处整个半球空间所有方向的入射光决定，一直往上追溯入射光

一直往上追溯入射光，成像所需的反射光是无数个反射方程之和

成像所需的反射光是无数个反射方程之和用积分表示，考虑到光源也会向此点发出光线，我们添加$L_{\theta }(x,\omega )$项，就得到了渲染方程
描述场景内各点照明情况的方程，即渲染方程
渲染方程满足能力守恒，是图形真实感的数学描述

如何求解渲染方程？
两边都有未知数

将此方程经过一番变换，写成离散的代数形式，有无穷项。

左边第一项是自发光项，第二项表示从光源出发后直接打到物体的所有光线（直接光），后面的项表示被其他物体反弹过来的光（间接光）

理论上光会反弹无数次，直到能量损耗为0

6.3 Global illumination（全局光照）

当直接光和间接光共同照亮场景就是所谓的全局光照（Global illumination）

现实世界都是全局光照，例如盒子映出墙壁的渐变色泽

例如复杂场景里的细腻反光

比如太阳无法直接照到的地方不至于一片漆黑

全局光照的本质：用离散方式逼近渲染方程

光栅化只有直接光，光源照不到的地方漆黑一片，只能手动补光模拟，但手动补光打破了能量守恒，成像效果依赖灯光师的水平
全局光照不仅有直接光，还有环境光，其意义在于部分消除了真实感渲染的主观性，它是在实打实地模拟现实

7. Real-time Global illumination

为什么实时如此难实现？
因为全局光照数学表达式中是无限项的组合，想要逼真必须实现很多间接光的反弹，这类技术当属光线追踪（一种全局光照技术）

7.1 Ray-Tracing（光线追踪）

光线从光源射出，碰到物体随机反弹，多次反弹后进入摄像机，形成一条光路，像素值由此时的光线决定

光源发出的光线大多数不会进入摄像机（如下图红色光线并没有进入摄像机），对成像并没有帮助，只会浪费算力

所以实际操作会从像素发射光线，多次反弹后找到光源，由于光路可逆，就可以等价成光源发出光线，摄像机接收

为了成像效果更好，通常会让每个像素发射多根光线，像素值是各光线数据的汇总

像素发射的光线越多，光线反弹得越多，渲染方程就更可能逼近，如果能实现无限次反弹，图像就能百分百准确。反弹次数能决定画质，却也会制约性能。

计算机判定每条光线被哪个三角形反弹只能靠计算，它会先求出光线和三角形的交点，再判断交点是否在三角形内，如果不在，说明光线不是被它反弹的

接着再让光线和第2个三角形做计算，如果该交点还不在第2个三角形内，那么就和第3个做计算等等

直到找到交点在内部的那个三角形


实时光线追踪的困难：高质量光照所要求的光线是每个像素发射几百根光线，目前算力每像素一根光线都做不到

7.2 Lumen

Lumen是虚幻引擎5的全动态全局光照和反射系统，专门针对下一代主机进行设计，是默认的全局光照和反射系统。Lumen能够在拥有大量细节的宏大场景中渲染间接漫反射，并确保无限次数的反弹以及间接高光度反射效果；无论是毫米级别的场景细节，还是数以千米的宏大场景，它都能应对得游刃有余。–引用自Lumen全局光照和反射

光线追踪主要慢在判断光线和三角形是否相交，在Lumen中引入一个概念解决了这个问题–距离场（Distance Field）
Distance Field（距离场）
取场景中的一个个位置点

计算位置点到离这个点最近物体的距离，再把这个距离数据存起来

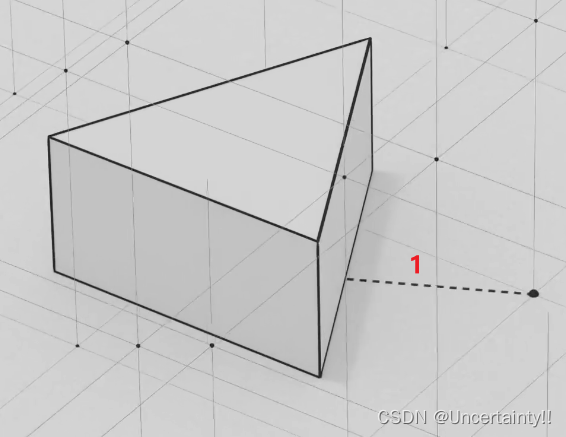
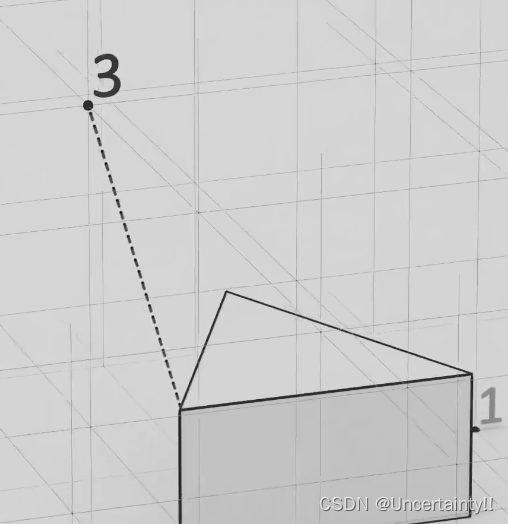
得到距离数值的集合–距离场

如何判断一条光线和谁相交？
光线打出去之后，让它走一段很短的路（步进），步进距离等于光源所在点（这个点是位置点吗？光线一定会通过位置点？）离它最近物体的距离

光线步进距离的逻辑：以距离为3的球体空间内一定没有物体存在，光线可以放心往前走（不会与其他物体相交）

如何知道光线与物体相交了？可以设置一个距离阈值，例如0.01，若光线离物体上的三角面的距离小于0.01则认为其相交了
若光线与最近物体上三角面的距离一直不小于阈值说明光线与任何物体都不相交

距离场每个位置点的数值是提前算好的，运行游戏时只需要查询每个步进点处的距离数据（并不做数学运算）很快就能确定与光线相交的物体了

如果场景中物体位置变了，就需要重新计算距离场

距离场的致命问题：距离场不包含材质信息，计算机只能依靠距离场得到光线与哪个物体相交，却由于获取不了材质无法完成光线反弹的计算，为解决这个问题引入了表面缓存（Surface Cache），用于快速查询场景中光线接触点的光照
Lumen会从多个角度捕获每个网格体的材质属性。这些捕获位置（即 卡（Cards） ）是针对每个网格体脱机生成的。

什么是表面缓存？
计算机为了存储光照专门分配的一个空间

Lumen全貌
实时全局光照的核心问题：如何实现无限次反弹的间接光？

无限次毕竟是理想状态，在实际应用中的实时全局光照技术

反射阴影贴图（Reflective Shadow Maps，RSM）
RSM的原理：让光线打到物体后将被照亮的位置当成光源再照亮整个场景

算法本质：比光栅化多了一次反弹和间接光

目前主流实时全局光照基本只提供一次反弹的间接光，并未真正逼近渲染方程，但一次反弹的全局光照也足够优秀


全局光照最终效果的贡献是随着光线反弹的次数依次递减的，这给实现无限次反弹提供了可能

Lumen最多只能产生一次反弹的间接光，为了弥补这一点，Lumen使用辐射度（Radiosity）来生成间接光
光照可以看作是多种效果的叠加，如果分开求解直接光和间接光会怎样？这是Lumen的思路

距离场不提供材质信息，材质未知光线该反射多少？无法判断

Lumen先将直接光存进表面缓存（Surface Cache）里，再想办法解决间接光，即用辐射度算法（Radiosity）解决。

辐射度算法（Radiosity）原理：将场景离散成一个个面元，一个面元向外辐射的能量一定等于其他面元辐射给它的能量之和

面元1接收到来自面元2的辐射
B2是面元2总共向外辐射的能量

F叫形状因子，可以理解成两个面元的空间关系

形状因子F决定了面元2向外的辐射有多大比例会被面元1接收

$\rho$是反射系数，表示面元1接收到的面元2的辐射，其中有多少又被辐射出去了

面元1向外辐射的能量

面元2向外辐射的能量

所有面元向外辐射的能量公式联立方程组

联立的方程组以求和符号简化，有的面元会发光需要单另加一个自发光项，不发光的面元该项为0


此方程组正是渲染方程在场景离散成面元后推导出来的，

将以上方程组经过转化就得到了我们熟悉的渲染方程离散形式

面元细分的越多，间接光的反弹次数就越多，成像效果就越好

只要求解出方程组就能实现所谓的无限次反弹的间接光

用传统光栅化将面元和摄像机相连，就可以用$B_j$连线所对应的像素值得到一张图像

面元越多方程就越多，怎么可能在一帧内求解这么多方程？

复用技术
相邻帧中变换的场景并不多，可以粗略认为大多数面元，它们每一帧接收的光照都差不多

相邻帧接收的光照都差不多

反弹次数越多的间接光，对最终光照结果贡献越小
面元的数量越多，间接光反弹的次数就越多
相邻帧间相比少部分变化的面元对整体光照结果影响并不大，这就是复用技术（Lumen实时全局光照的基础）

刚开始（第0帧）所有面元只接受到了来自光源的直接光，没有间接光，将第0帧的光照存入表面缓存

第1帧中直接光仍从光源采集，间接光则是其他面元向面元1的辐射

第0帧和第1帧是相邻帧，也就是从第0帧到第1帧整体光照变化不大，我们可以将第0帧复用给第1帧，所以表面缓存就是两帧画面的光照中转站

直接光加间接光就是面元1在第1帧的最终光照，仍将它存进表面缓存和第0帧的最终光照累加更新这个数值

将第1帧的最终光照当成第2帧的间接光+第2帧的直接光，更新表面缓存

随着帧数的增加，每个面元接收的光照也会累积更新，结果将越来越准确，其他面元也是如此

每个面元在每一帧的光照都可以这样采集。

Lumen巧妙地利用了第0帧面元直接光是已知的特性，对每个面元进行单独求解，规避了传统辐射度算法联立方程组求解未知数的难度，后续每一帧里的迭代计算则保证了计算的准确性，这也是无线反弹的真正内涵，也是Lumen的核心思路

生成光照后，还需将它采集给摄像机进行成像，为了提高效率，Lumen根据到摄像机的距离，将场景分成4个区域，每个区域的光照采集有对应的加速方案

Lumen的厉害之处在于，它通过融合两种经典全局光照思路，以及一系列巧妙的工程手段解开了原本无法直接求解的渲染方程