深度学习中的潜在空间

1 潜在空间定义

Latent Space 潜在空间：Latent ，这个词的语义是“隐藏”的意思。“Latent Space 潜在空间”也可以理解为“隐藏的空间”。Latent Space 这一概念是十分重要的，它在“深度学习”领域中处于核心地位，即它是用来学习数据的潜在特征，以及学习如何简化这些数据特征的表达，以便发现某种规律模式，最终来识别、归类、处理这些数据。

形式上，潜在空间被定义为抽象的多维空间，它编码外部观察事件的有意义的内部表示。在外部世界中相似的样本在潜在空间中彼此靠近。

为了更好地理解这个概念，让我们考虑一下人类如何感知世界。通过将每个观察到的事件编码为我们大脑中的压缩表示，我们能够理解广泛的主题。例如，我们不会记住狗的每一个外观细节，以便能够在街上认出一只狗。正如我们在下图中所看到的，我们保留了狗的一般外观的内部表示：

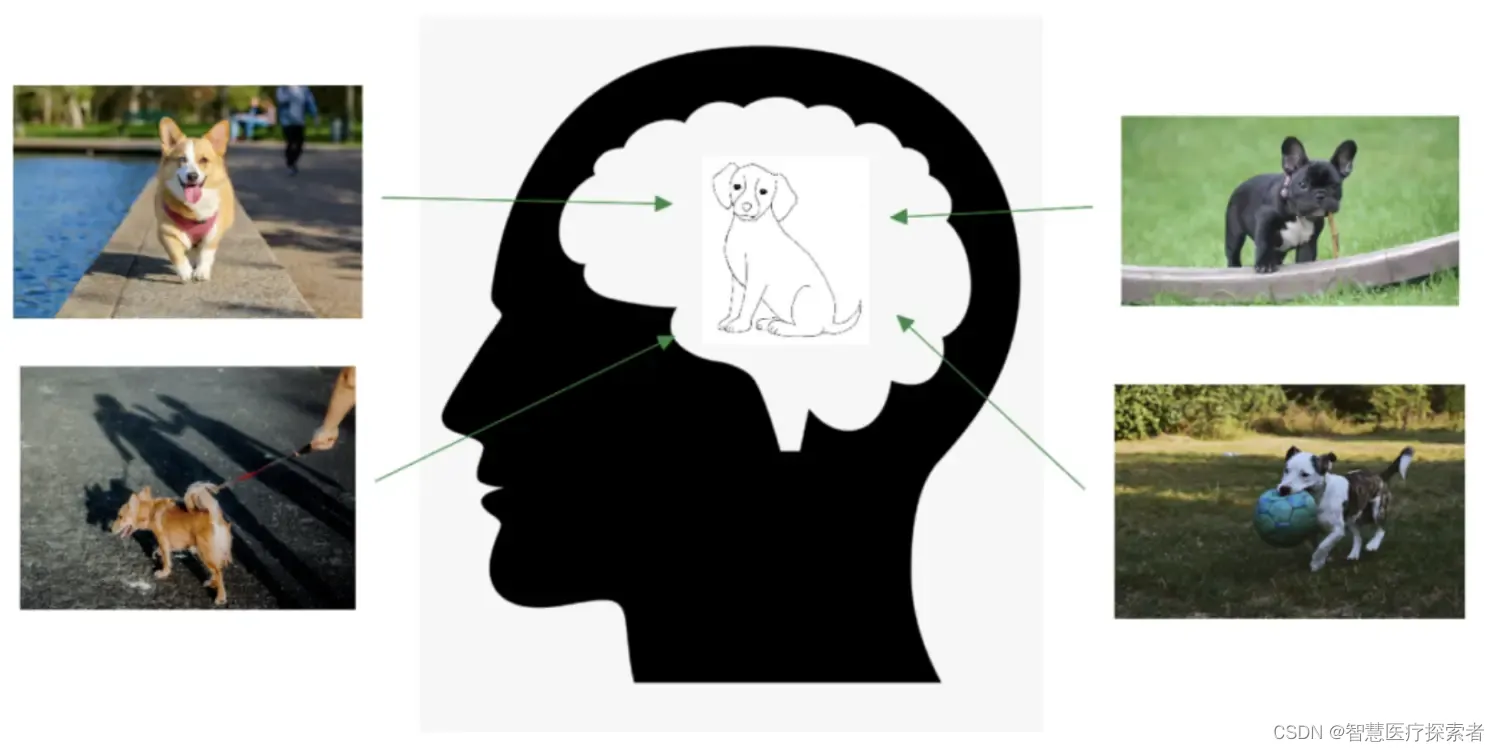
以类似的方式，潜在空间试图通过空间表示向计算机提供对世界的压缩理解。

2 潜在空间的重要性

深度学习已经彻底改变了我们生活的许多方面，其应用范围从自动驾驶汽车到预测严重疾病。它的主要目标是将原始数据（例如图像的像素值）转换为合适的内部表示或特征向量，学习子系统（通常是分类器）可以从中检测或分类输入中的模式。因此，我们意识到深度学习和潜在空间是密切相关的概念，因为前者的内部表示构成了后者。

正如我们在下面看到的，深度学习模型将输入原始数据并输出位于称为潜在空间的低维空间中的判别特征。然后使用这些特征来解决各种任务，如分类、回归或重建：

为了更好地理解潜在空间在深度学习中的重要性，我们应该思考以下问题：为什么我们必须在分类、回归或重建之前在低维潜在空间中对原始数据进行编码？答案是数据压缩。具体来说，在我们的输入数据是高维的情况下，不可能直接从原始数据中学习重要信息。例如，在图像分类任务中，输入维度可能与输入像素相对应。系统似乎不可能通过查看如此多的值来学习有用的分类模式。解决方案是使用深度神经网络将高维输入空间编码为低维潜在空间。

3 实例

通过一些例子，理解潜在空间的存在对于捕获任务复杂性和实现高性能是必要的。

3.1 图像特征空间

正如我们之前提到的，潜在空间是每个卷积神经网络不可或缺的一部分，它以图像的原始像素作为输入，并在最后一层对潜在空间中的一些高级特征进行编码。这个潜在空间使模型能够使用低维判别特征而不是高维原始像素来执行任务（例如，分类）。在下图中，我们可以看到 CNN 的一般架构：

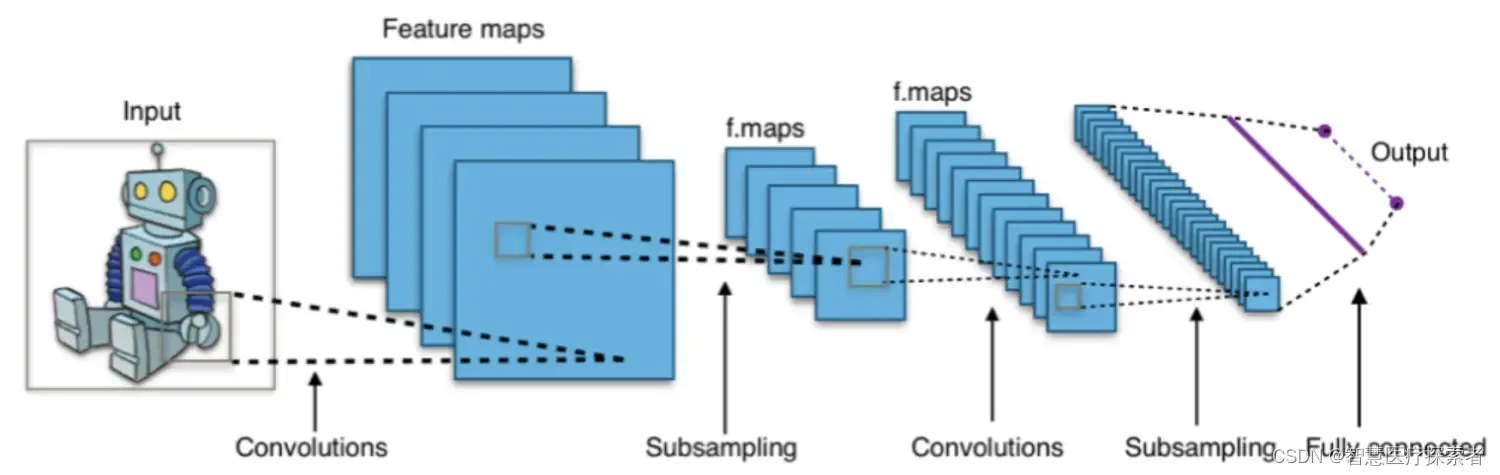
训练后，模型的最后一层捕获了图像分类任务所需的重要输入模式。在潜在空间中，描绘同一对象的图像具有非常接近的表示。通常，潜在空间中向量的距离对应于原始图像的语义相似性。

下面，我们可以看到动物分类模型的潜在空间是怎样的。绿色点对应于从模型的最后一层提取的每个图像的潜在向量。我们观察到相同动物的向量更接近潜在空间。因此，模型更容易使用这些特征向量而不是原始像素值对输入图像进行分类：

3.2 词嵌入空间

在自然语言处理中，词嵌入是词的数字表示，因此相似的词具有接近的表示。因此，词嵌入位于一个潜在空间中，每个词都被编码成一个低维语义向量。有许多学习词嵌入的算法，如 Word2Vec 或 GloVe。在下图中，我们可以看到潜在空间中词嵌入的拓扑图：

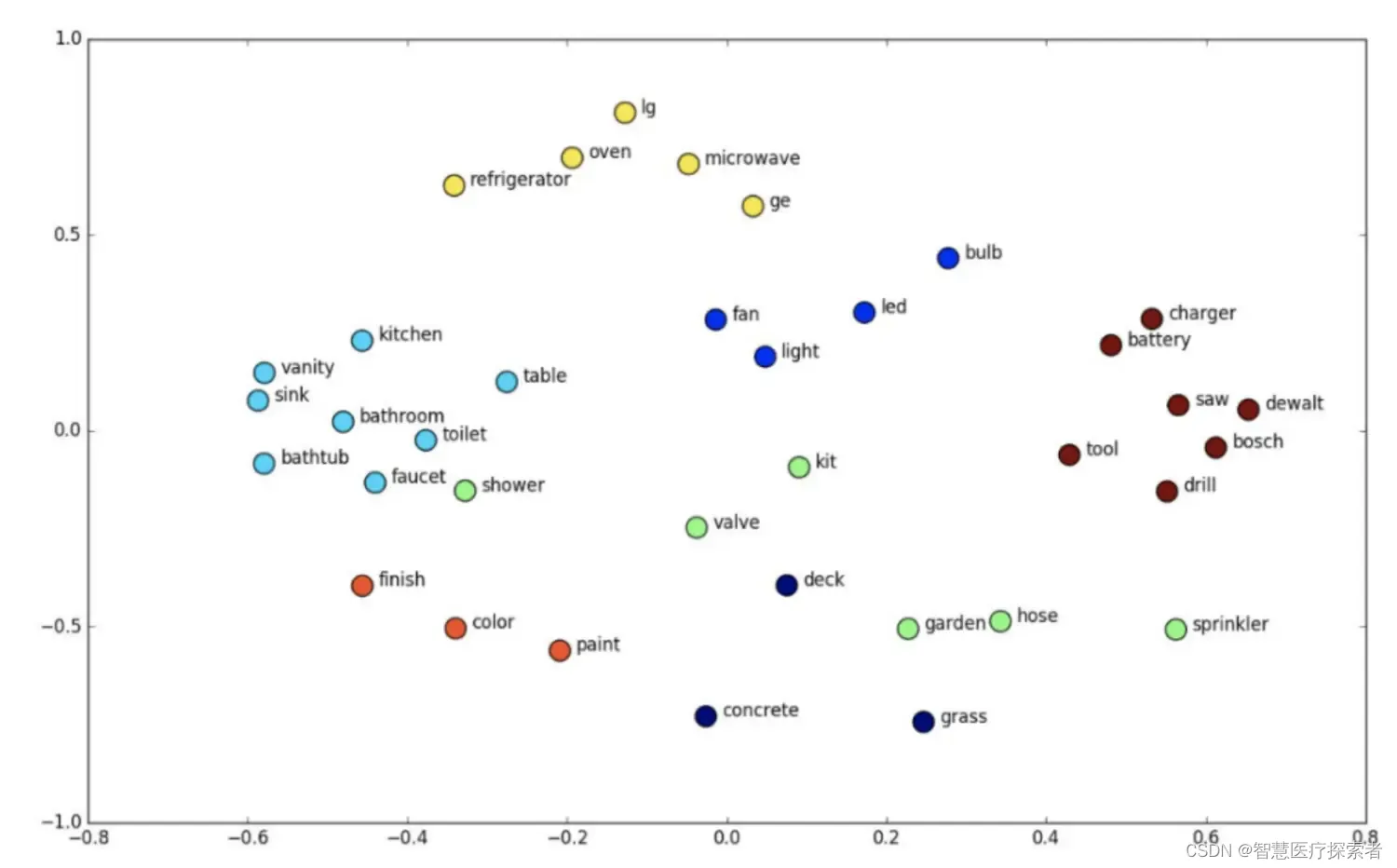
正如预期的那样，语义相似的词，如“toilet”和“bathroom”，在潜在空间中有紧密的词嵌入。

3.3 GANs

GAN 将来自某些先验分布和输出的随机向量作为输入和图像。该模型的目标是学习生成真实数据集的底层分布。例如，如果我们的数据集包含带椅子的图像，则 GAN 模型会学习生成带椅子的合成图像。GAN 的输入充当潜在向量，因为它将输出图像编码为低维向量。为了验证这一点，我们可以看到插值在潜在空间中是如何工作的，因为我们可以通过线性修改潜在向量来处理图像的特定属性。在下图中，我们可以看到如何通过改变生成人脸的 GAN 的潜在向量来处理人脸的姿势：

3.4 变分自编码器（VAE）

变分自编码器（Variational Autoencoder，VAE）是深度学习中一种强大的生成模型，它在处理数据生成和潜在空间探索方面具有广泛的应用，可用于处理各种类型的数据并解决多样的机器学习问题，如图像生成、音频生成、数据降维、异常检测等。VAE不仅可以有效地学习数据的紧凑表示，还可以生成具有连续分布的新样本，使其在图像生成、无监督学习和生成对抗网络（GAN）等领域大放异彩。

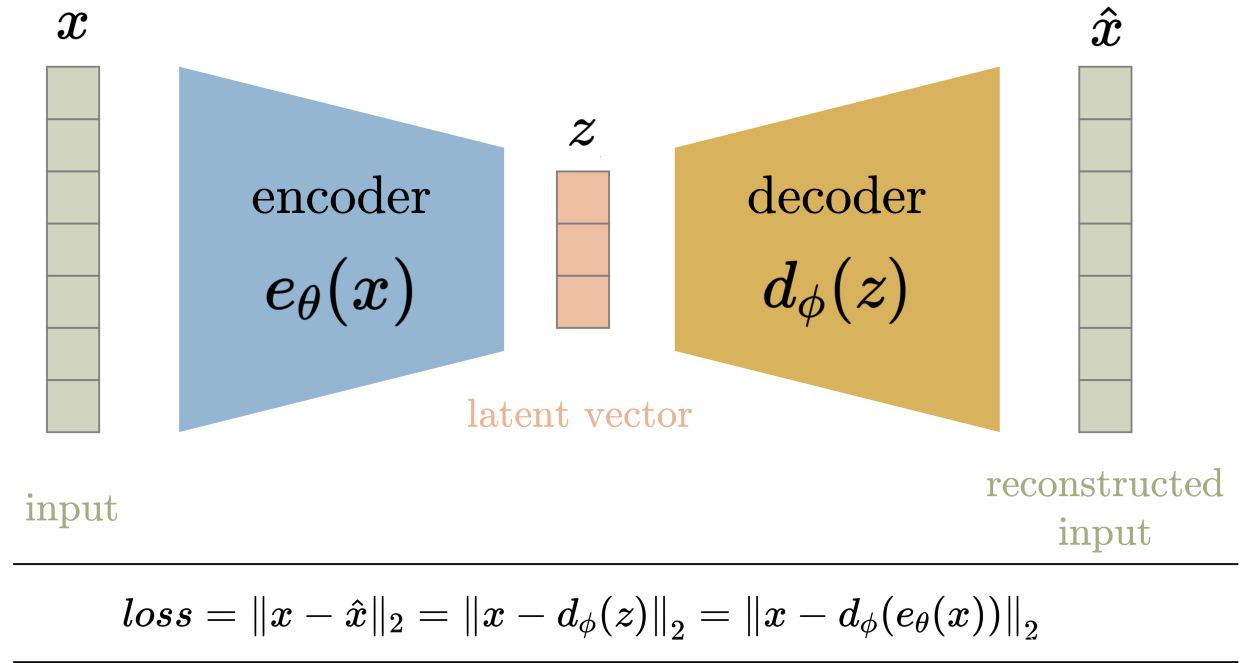
VAE的核心思想是引入潜在变量（Latent Variables）来表示数据的分布。与传统自编码器不同，VAE并不直接学习数据的确定性表示，而是学习数据的概率分布。下面是VAE的基本原理：

• 编码器（Encoder）：编码器将输入数据映射到潜在空间中，产生潜在变量的均值和方差。这两个参数用于定义一个潜在空间中的概率分布。

• 潜在变量采样（Sampling）：从概率分布中采样一个潜在变量，这个变量代表了输入数据的潜在表示。采样过程通常使用正态分布或其他分布来实现。

• 解码器（Decoder）：解码器接受采样后的潜在变量，并将其映射回原始数据空间，生成重建数据。

• 损失函数（Loss Function）：VAE的损失函数包括两部分，一部分是重建误差，用于测量重建数据与原始数据的差异；另一部分是潜在空间的正则化项，通常使用KL散度来度量潜在变量的分布与标准正态分布之间的差异。

VAE的一个重要特点是它学习到的潜在空间是连续的，这意味着在潜在空间中的插值产生具有语义连续性的结果。例如，在图像生成任务中，通过在潜在空间中进行插值，可以平滑地从一个样本过渡到另一个样本，而不会产生不连续的效果。