代码训练营Day.15 | 102. 二叉树的层序遍历、226. 翻转二叉树、101. 对称二叉树
102. 二叉树的层序遍历
1. LeetCode链接
2. 题目描述
如题。
3. 解法
1. 迭代法
? ? ? ? 这个不是普通的利用队列实现的层序遍历,难点在于同一层的节点数值要包在一起。
? ? ? ? 暴力一点,就是记录每一层的节点数目,然后用for循环在这个数目是打住。如何记录每一层的节点数目?
? ? ? ? 我们只要知道上一层有多少节点就行,因为,在将某一节点的左右孩子压入队列时,如果有孩子,那这一层的节点数目就++,这样层层往下。而第一层的数目永远知道。
? ? ? ? 之后还有一个偷懒小技巧。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> results;
queue<TreeNode*> qu;
if (root == NULL) return results;
int f_size = 1;
qu.push(root);
while (!qu.empty()) {
// TreeNode* cur = qu.front();
vector<int> result;
int z_size = 0;
for (int i = 0; i < f_size; i++) {
TreeNode* cur = qu.front();
result.push_back(cur->val);
qu.pop();
if (cur->left != NULL) {
qu.push(cur->left);
z_size++;
}
if (cur->right != NULL) {
qu.push(cur->right);
z_size++;
}
}
results.push_back(result);
f_size = z_size;
}
return results;
}
};这里有一个偷懒小技巧:因为其实每层的节点数目,就等于队列长度,(上一层的已经全pop掉了,下一层的还没开始),所以不用额外空间记录每层长度。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};2. 递归法
????????这道题用递归法就很巧。
????????前序遍历的递归方法你应该很熟了,基本上递归的逻辑顺序就是前序遍历的顺序。而前序遍历有什么特点?尤其是在每一层的维度上看,其实就是每一层的节点从左到右依次遍历。那么我们只要记录节点所在层数就行。
? ? ? ? 双层数组中,如果某一结点的层数不在双层数组中,则创建该层的一维数组。否则,直接在对应层push_back.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void order(TreeNode* root, vector<vector<int>>& results, int depth) {
if (root == NULL) return;
if (results.size() == depth) results.push_back(vector<int>());
results[depth].push_back(root->val);
order(root->left, results, depth + 1);
order(root->right, results, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> results;
int depth = 0;
order(root, results, depth);
return results;
}
};????????
226. 翻转字符串
1. LeetCode链接
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2. 题目描述


3. 想法
??????? 做完之前的层序遍历,乍一看可以在上一层节点下,倒叙连接下一层的节点。(与层序遍历不同的是,这里也要同时记录NULL孩子节点,注意避免NULL->left)
??????? 但是如果利用vector这样搞的话,需要在执行倒叙连接操作后,将该层对应vector也倒叙排列。这个方法可行,但其实绕了远路。
??????? 注意看反转后二叉树的特点,事实上就是,任意节点的左右孩子互换问题。
??????? 这样想的话,就可以通过简单遍历二叉树,反转每个节点的左右孩子。
前序递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
TreeNode* node;
invertTree(root->left);
invertTree(root->right);
node = root->left;
root->left = root->right;
root->right = node;
return root;
}
};///层序迭代法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> qu;
if (root == NULL) return root;
qu.push(root);
while (!qu.empty()) {
int f_size = qu.size();
for (int i = 0; i < f_size; i++) {
TreeNode* cur = qu.front();
TreeNode* swap;
qu.pop();
if (cur == NULL) continue;
qu.push(cur->left);
qu.push(cur->right);
swap = cur->left;
cur->left = cur->right;
cur->right = swap;
}
}
return root;
}
};101. 对称二叉树
1. LeetCode连接
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2. 题目描述

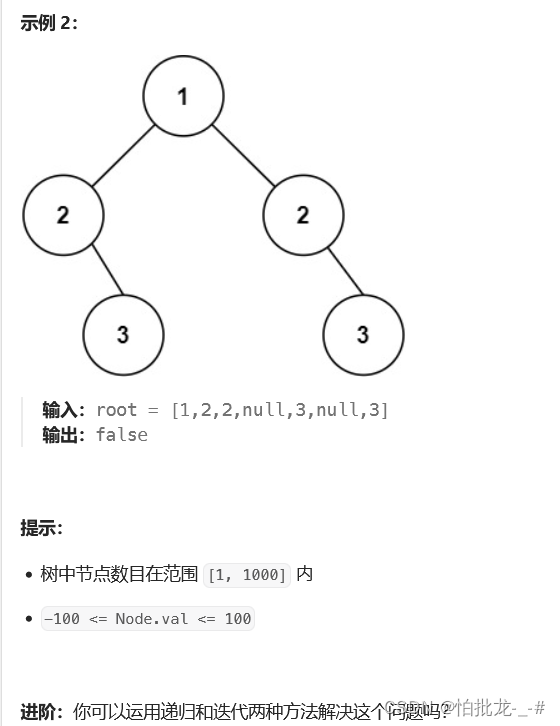
3. 解法
??????? 真男人要用多种解法。碎碎念,二叉树的揭发好像都不少。
1. 迭代法
??????? 我首先想到比较笨的方法是改写层序遍历,或者说上一题——翻转二叉树。需要利用一个额外的vector记录每层的值,然后判断这个vector是否对称即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode*> qu;
if (root == NULL) return root;
qu.push(root);
while (!qu.empty()) {
vector<int> result;
int f_size = qu.size();
for (int i = 0; i < f_size; i++) {
TreeNode* cur = qu.front();
TreeNode* swap;
qu.pop();
if (cur == NULL) {
result.push_back(111);
continue;
} else result.push_back(cur->val);
qu.push(cur->left);
qu.push(cur->right);
}
vector<int> aa = result;
reverse(result.begin(), result.end());
if (aa != result) return false;
}
return true;
}
};???????? 巧妙解法是,该题其实就是判断两棵树是否翻转对应。用队列来层序遍历两棵树。一棵树从左到右遍历,另一棵树从右到左遍历。同步遍历时,如果两棵树满足翻转关系,则当前两个指针的值必相等。(事实上,把队列换成栈仍然可以,代码几乎无改动)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode*> qu;
TreeNode* left = root->left;
TreeNode* right = root->right;
qu.push(left);
qu.push(right);
while (!qu.empty()) {
left = qu.front();
qu.pop();
right = qu.front();
qu.pop();
if (left == NULL && right == NULL) continue;
else if (right == NULL || left == NULL || left->val != right->val) return false;
qu.push(left->left);
qu.push(right->right);
qu.push(left->right);
qu.push(right->left);
}
return true;
}
};2. 递归法
??????? 既然可以用栈来迭代法,那就可以用递归。整体逻辑还是判断两棵树翻转对应。
??????? 设计一个判断两颗树是否翻转对应的函数。递归出口是两棵树都是NULL,返回true;两节点本身不对应则返回false;左树的左子树和右树的右子树继续递归判断;左树的右子树和右树的左子树继续递归判断。整体如下。
??????? 1. 确定参数和返回值。参数:两个树节点;返回值:两个树节点表示的两棵树是否对应翻转。
??????? 2. 终止条件。递归出口是两棵树都是NULL,返回true;两节点本身不对应则返回false。
??????? 3. 单层递归逻辑。左树的左子树和右树的右子树继续递归判断;左树的右子树和右树的左子树继续递归判断。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isReverse(TreeNode* left, TreeNode* right) {
if (left == NULL && right == NULL) return true;
if (left == NULL || right == NULL || left->val != right->val) return false;
return isReverse(left->left, right->right) && isReverse(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
TreeNode* left = root->left;
TreeNode* right = root->right;
return isReverse(left, right);
}
};????????
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!