深度学习 | 基础卷积神经网络

????????卷积神经网络是人脸识别、自动驾驶汽车等大多数计算机视觉应用的支柱。可以认为是一种特殊的神经网络架构，其中基本的矩阵乘法运算被卷积运算取代，专门处理具有网格状拓扑结构的数据。

---

1、全连接层的问题

1.1、全连接层的问题

??????? “全连接层”的特点是每个单元之间连接所有的前一层单元。这种连接方式使得全连接层能够学习到输入数据之间的非线性关系，并能够在神经网络中扮演重要的角色。

?????????

????????但是，全连接层也存在一些主要问题，这些问题主要表现在以下几个方面：

????????1、参数数量巨大：全连接层中的参数数量随着输入和输出单元数量的增加而急剧增加。这会导致训练时间增加，并且很容易导致过拟合。

????????举个例子：假设我们有一个全连接层，该层具有 1000 个输入单元和 100 个输出单元

??????? 意味着该层中有? 1000x100 = 100000 个权重参数和 100 个偏置参数。这对于较小的神经网络来说可能不是问题，但是对于规模较大的神经网络来说，参数数量的增加可能会导致训练时间增加，并且很容易导致过拟合。

????????例如，如果我们在该层之后再添加一个具有 100 个输入单元和 10 个输出单元的全连接层，则该层中将有 100*10=1000 个权重参数和 10 个偏置参数。这样，我们的神经网络中就有 101000 个参数。如果我们再添加几层全连接层，参数数量将会进一步增加。

????????可以看出，当神经网络中包含许多全连接层时，参数数量可能会变得非常庞大，这对于训练和推理来说都是挑战。

????????2、对空间不友好：全连接层对输入数据的空间属性没有任何假设，这意味着它不能很好地处理空间相关的数据。例如，图像数据中的像素是有空间位置关系的，而全连接层无法很好地利用这种关系。

????????3、对小型数据集不友好：由于全连接层中的参数数量非常庞大，因此在训练数据较少的情况下，很容易导致过拟合。

????????4、对计算资源不友好：全连接层中的大量参数意味着它需要大量的计算资源进行训练和推理。这对于计算资源有限的系统来说是一个挑战，尤其是在模型规模较大的情况下。

??????? 5、对于序列数据不友好：全连接层无法很好地处理序列数据，因为它无法保留序列中各个元素之间的顺序信息。例如，在处理文本数据时，单词的顺序是非常重要的，但全连接层无法保留这种顺序信息。

1.2、多层感知机的局限

????????前面学习的多层感知机，也就是仅仅使用全连接层的深度神经网络，除了上述问题外，在处理实际应用的时候还有很多局限。例如，人工智能试图解决的一大类问题都涉及到图像处理。而多层感知机在这方面遇到了两个显著的困难：平移不变性和局部性问题。

????????1. 平移不变性 （Translation Invariance）

????????它指的是模型对输入数据的平移不敏感。

????????例如，考虑一张 n 维的输入数据和一个平移矩阵 T ，其中 T 是一个 nxn 的矩阵。

????????对于一个平移不变的模型?，对于任意的 x 和 T ，都有 f(x) = f(Tx)。

????????这意味着，如果我们将输入数据 x 平移一小段距离，则模型应该能够正确地识别输入中的对象。

????????举个例子来说，在图像分类任务中，如果我们将一张图像平移一小段距离，则模型应该能够正确地识别图像中的对象。

????????

????????但是，多层感知机很难学习到这种平移不变性，因为它们是由许多全连接层组成的，其中每层的权重参数都是固定的。因此，多层感知机很难对输入数据的平移进行建模。

????????2. 局部性

????????局部性是指模型对输入数据的局部信息敏感。

????????这是神经网络中非常好的一个特性，因为在许多应用中，输入数据通常包含大量局部信息，而这些局部信息往往可以帮助我们识别数据中的模式。

????????比如图像分类任务中，可以借助图像局部信息识别对象。

????????然而遗憾的是，多层感知机很难学习到这种局部性。为什么呢？

????????因为它们是由许多全连接层组成的，其中每层的权重参数都是固定的。这意味着，多层感知机无法从输入数据的局部信息中学习到有用的特征。

????????还是以图像分类任务来说，假设我们有一张图像，其中包含一个狗的头部，这是想要识别的目标对象。如果我们使用的是多层感知机来进行图像分类，那么需要将整张图像输入到模型中，并期望模型能够从图像的整体信息中识别出狗的头部。然而，由于多层感知机没有学习到局部性的能力，因此很难做到这一点。

?????????

????????正是上述问题，促使科学家们思考如何改进多层感知机这样都是全连接层的网络。由此发展出来了卷积神经网络等一系列更加强大的高级模型。想要学好卷积神经网络，先要从什么是卷积开始。

---

?2、图像卷积

????????

2.1、卷积

????????卷积其实是一种数学运算，常用于信号处理和图像处理领域。

????????它的基本思想是将一个函数与另一个函数进行点积，并通过滑动窗口的方式计算整个输入数据的值。一维卷积的数学表示如下：

????????

????????其中 f 和 g 分别表示输入函数和卷积核函数，*? 表示卷积运算符，t 表示时间，τ 表示滑动窗口的位置。

????????二维卷积的数学公式类似，如下所示：

????????

????????其中 f 和 g 分别表示输入函数和卷积核函数，*? 表示卷积运算符，x 和 y 表示二维平面上的位置，x' 和 y' 表示滑动窗口的位置。

??????? 卷积值通常称为特征映射。

????????

---

2.2、图像卷积

????????在图像处理中，卷积通常用于图像卷积和图像滤波。

????????图像卷积是指将图像与卷积核进行卷积运算，从而得到新的图像。

????????

????????

---

2.3、互相关运算和卷积运算

*** 存疑

?????????在图像卷积中，这两个数学概念经常容易混淆。互相关运算（cross-correlation）的数学定义如下：

????????

????????其中，I 是输入图像，K 是卷积核，* 是互相关运算的符号，?(x，y)是输出图像中的像素坐标。

????????真正的卷积运算（convolution）数学公式：

????????

????????二者是不是长的很像，只差了一个正负号，卷积和互相关相比加号变成了减号。

????????严格说在数学上它们是不同的运算，但是在图像处理领域，两者差别就没那么明显了，或者说反而产生了混用现象。

????????我们用一个例子来加以说明。

????????先看互相关运算，下图左边为原始图像，它和一个卷积核做互相关运算后得到右边的输出图像。

????????

????????卷积核在左边图像上滑动，同时做互相关运算，也就是对应元素相乘在相加。由于原图像多数元素都为0，只在输入图像中心为1，因此最后输出了右边图像。结果显示相当于把卷积核进行了180度翻转。

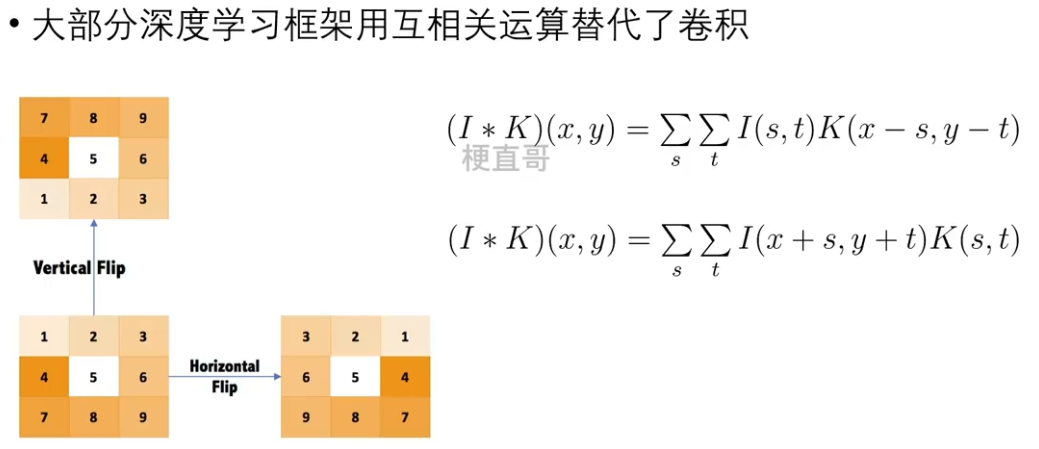
????????再来看卷积运算，公式中它和互相关相比改变了符号，体现在图像上就是先把卷积核进行了180度翻转，或者说就是先左右翻转，然后上下翻转，然后再进行互相关运算。如下图所示：

????????

????????由于卷积运算相当于翻转了两次，因此最后输出图像中还是123456789这样的顺序，而互相关运算只翻转了一次，最终结果变成了987654321这样的形式。

????????虽然两种运算看似不同，但由于卷积核是自己定的，本身没有顺序上的限制，所以完全可以用翻转过的卷积核，这样以来二者就没啥区别了。也正是因为这个原因，大部分深度学习框架在代码实现的时候偷了懒，干脆用了互相关运算替代了卷积。因此严格意义上说，卷积层用的是互相关运算，但依然被叫成了卷积。

????????

---

2.4、图像卷积的作用

????????

---

3、卷积层

?????????

??????? 应用了图像卷积操作的神经网络隐藏层。

????????卷积层的主要作用是提取输入数据的局部特征，并将这些局部特征抽象为更高级的特征。

? ????? Filter 滤波器也就是核函数。

????????

??????? 对比经典的神经元模型：

????????????????

3.1、图像内核的效果：

????????Image Kernels explained visually

3.2、感受野（Receptive Field）

??????? 感受野就是 对外界输入信息有相应的区域，是指输入张量中卷积层特征映射中的每个元素所能“感受”到的区域。

????????例如，假设输入张量的大小为 H x W ，内核大小为 k x k，那么卷积层的感受野大小就为 k x k。

????????举个例子，假设输入张量是一张 5x5 的图像，卷积层使用 3x3 的内核，stride 1 为?，padding 为 0 ，那么卷积层的输出张量大小为 3x3 ，感受野大小为 3x3 。

??????? 在计算机视觉当中，就是卷积核的大小；

??????? 在生物学中，就是神经元的刺激反应范围。

????????

3.3、卷积层和全连接层区别

??????? 卷积核大小限制放松了，卷积核可滑动 ~

????????

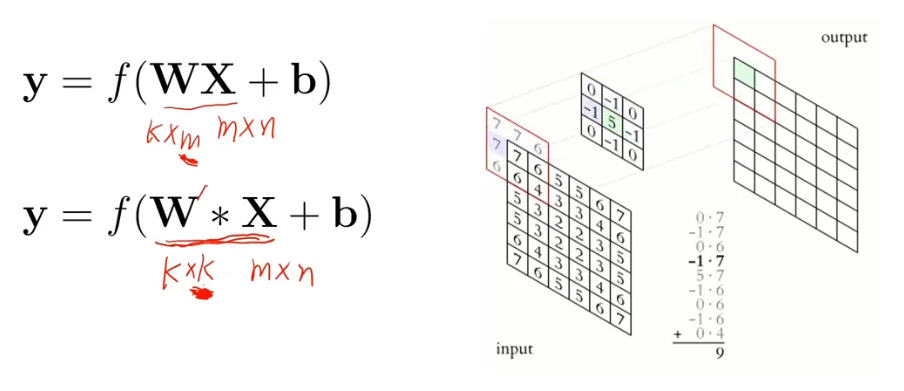
????????卷积层的输入是一个多维数组，而全连接层的输入是一个向量。

3.4、卷积层的性质

???????? 1、稀疏交互

??????? ***? 存疑

????????Sparse Interaction：核的大小远远小于输入的大小，连接变少，交互更加稀疏。

??????? 从而可以通过只有几十个或上百个像素点的图像内核，图像内核本身可以变得很小，来检测很小但是更加有意义的图像特征，就像拿着放大镜去看。

??????? 输入图像可能是非常大的，因此他就减少了对模型参数的存储，大大提高了统计的效率。

????????

???????? 2、参数共享

?????????Parameter Sharing: 空间不同位置共享同样的参数（内核小窗口滑动）。

????????共享权值的方式意味着，同一个卷积层内的所有节点都使用相同的权值。这与全连接层不同，全连接层中的每个节点都有一个独立的权值。因此卷积层的参数数量要比全连接层少得多。

????????显著降低模型参数存储需求，提高统计效率。

????????

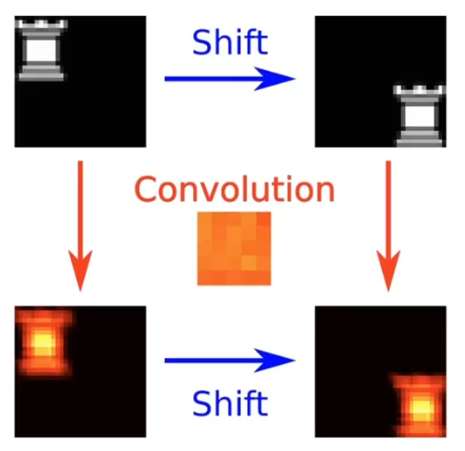
???????? 3、平移相等性（平移等变）

?????????Translation Equivariance

????????输入变化，输出跟着相同变化。

??????? 假定 f 是特征，g 是变换，用公式表示：

????????????????

??????? 即先提取特征再进行变换和 先进行变换在提取特征 没什么区别。

????????

---

3.5、卷积层常见操作

3.5.1、Padding 填充

?????????如果卷积核和输入图像尺寸不同，输出图像的大小就不能与输入图像保持一致了。为了解决这个问题，人们想出了很简单但是实用的办法，就是填充（padding）操作。

??????? 卷积内核越界时，采用填充。

??????? padding = (卷积核大小 - 1) / 2

????????

????????使用填充时的注意事项：

• 在使用 padding 时，你需要确定 padding 的大小。一般来说，padding 的大小应该是卷积核的大小的一半。例如，如果卷积核的大小是 3x3，则 padding 的大小应该是 1。这样，卷积核就可以对输入图像的所有像素进行卷积运算，而不会忽略边缘像素。

• 在使用 padding 时，输入图像的大小会变大。这可能会导致模型的计算量增加，并可能需要更多的存储空间。因此，你需要考虑是否真的需要使用 padding，或者是否可以使用更小的 padding 大小。

• 在使用 padding 时，输出图像的大小也会变大。这可能会导致模型的计算量增加，并可能需要更多的存储空间。因此，你需要考虑是否真的需要使用 padding，或者是否可以使用更小的 padding 大小。

• 在使用 padding 时，你可能需要使用更多的卷积层来捕捉更多的特征。因为使用 padding 后输入图像的大小会变大，所以你可能需要使用更多的卷积层来提取图像的特征。

3.5.2、Stride 步长

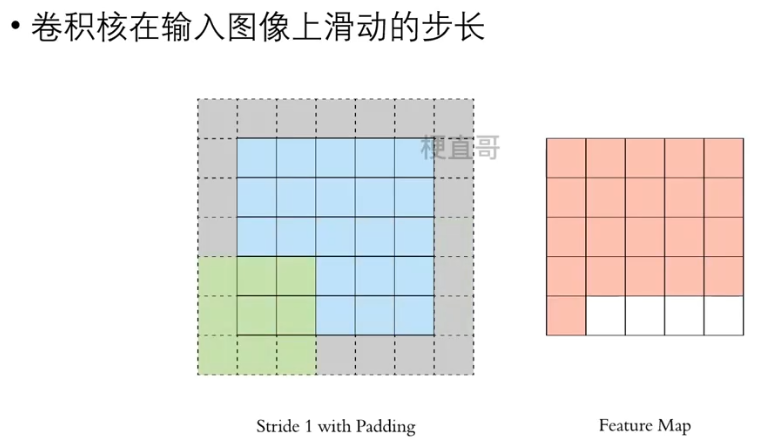
????????调整步长可以改变卷积核在输入图像上滑动的距离，

????????导致卷积核对输入图像进行卷积运算的次数减少，输出图像大小成倍减小，但是可能导致信息丢失。

????????此外，步长还可以用于控制卷积核的步长在输入图像的哪一维方向滑动。

????????例如，假设我们有一个 4x4 的输入图像和一个 3x3 的卷积核。如果我们设置步长为 (1, 2)，则卷积核会在输入图像的行方向滑动 1 个像素，在列方向滑动 2 个像素。这样，卷积核会对输入图像进行 4 次卷积运算，并产生一个 2x2 的输出图像。

????????

代码实现：

import?torch

#?创建输入图像
input_image?=?torch.tensor([[1,?2,?3,?4],
????????????????????????????[5,?6,?7,?8],
????????????????????????????[9,?10,?11,?12],
????????????????????????????[13,?14,?15,?16]])

#?创建卷积核
kernel?=?torch.tensor([[0,?1,?0],
???????????????????????[1,?1,?1],
???????????????????????[0,?1,?0]])

#?使用步长为?1?进行卷积运算
output_image?=?torch.conv2d(input_image.unsqueeze(0).unsqueeze(0),?kernel.unsqueeze(0).unsqueeze(0),?stride=1,?padding=1)
print("Output?image?with?stride=1:")
print(output_image)?

#?使用步长为?2?进行卷积运算
output_image_strided?=?torch.conv2d(input_image.unsqueeze(0).unsqueeze(0),?kernel.unsqueeze(0).unsqueeze(0),?stride=2,padding=1)
print("Output?image?with?stride=2:")
print(output_image_strided)??

#?使用步长为?3?进行卷积运算
output_image_strided?=?torch.conv2d(input_image.unsqueeze(0).unsqueeze(0),?kernel.unsqueeze(0).unsqueeze(0),?stride=3)
print("Output?image?with?stride=3:")
print(output_image_strided)??

Output image with stride=1:
tensor([[[[ 8, 12, 16, 15],
          [21, 30, 35, 31],
          [37, 50, 55, 47],
          [36, 52, 56, 43]]]])
Output image with stride=2:
tensor([[[[ 8, 16],
          [37, 55]]]])
Output image with stride=3:
tensor([[[[30]]]])

3.6、卷积常见参数关系

????????卷积层的特征映射（feature map）是指卷积层对输入数据进行卷积后得到的输出张量。????????

????????特征映射中的每个元素都是输入张量中相应区域的卷积和，其中区域的大小和形状由卷积层的内核大小决定。

?????????

??????? 为什么不用 奇数 x 偶数，偶数 x 偶数 的卷积核呢？

??????? 这是由于 奇数 x 奇数 的卷积核 更容易进行padding，而且更容易找到卷积的锚点。

3.7、多通道卷积

????????

??????? 每个滤波器 Filter 都是卷积核的一个集合。

????????

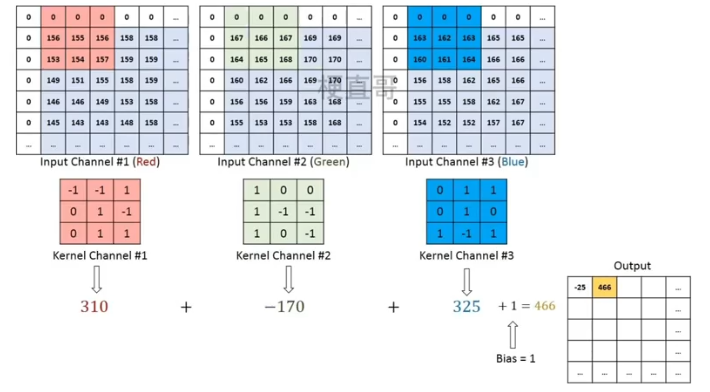
??????? 输入通道数 = 卷积核通道个数

????????

??????? 滤波器个数 = 输出通道数

????????

??????? 最后输出 feature map。

---

3.8、分组卷积

?????????

????????从上图可以看出，一般的卷积会对输入数据的整体一起做卷积操作，

????????即输入数据：H1×W1×C1；

??????? 而卷积核大小为h1×w1，一共有C2个，即共有C2个h×w×c1的滤波器，

????????然后卷积得到的输出数据就是H2×W2×C2。

????????这里我们假设输出和输出的分辨率是不变的。主要看这个过程是一气呵成的，这对于存储器的容量提出了更高的要求。?

????????

?? ? ?? 如果将输入 feature map 按通道分为 g 组，则每组特征图的尺寸为 ，

? ? ??? 每组对应的滤波器卷积核的 尺寸 为? ，

? ? ??? 每组的滤波器数量为? 个，滤波器总数依然为 C2 个。

?? ? ?? 每组的滤波器只与其同组的输入 map 进行卷积，每组输出特征图尺寸为 ，

??????? 将 g 组卷积后的结果进行拼接 (concatenate) ，

????????得到最终的得到最终尺寸为? 的输出特征图。

---

?4、池化层 Pooling

??????? 本质就是采样，用来压缩信息。

??????? 将输入的特征映射到更小的特征空间中，从而使网络结构变得更加紧凑。

????????如果没有池化层，网络的参数数量就会变得非常大，这会导致训练时间变长，并且容易出现过拟合现象。

????????池化层通过下采样的方式实现了信息的压缩，减少了网络的参数数量，这有助于缩短训练时间，并且可以防止过拟合。

????????这里，下采样是指将输入的特征缩小为原来的一部分。此外，池化层还可以帮助网络学习更加抽象的特征，从而提升分类的准确率。

????????总体而言，池化层在卷积神经网络中起到了信息压缩的作用，减少了参数的数量，防止过拟合，并且可以帮助网络学习更加抽象的特征。

4.1、卷积网络典型结构

??????? 分类问题会加上一层 softmax。

????????

4.2、最大池化 Max Pooling

????????使用邻域内最大值来代替网络在该位置的输出

????????

4.3、平均池化 Average Pooling

???????? 求区域（滤波器 / 窗口）的平均值。

????????

????????最大池化层可以帮助网络学习更强的特征，而平均池化层可以帮助网络学习更平滑的特征。二者都可以帮助网络学习更强的特征，同时还可以防止过拟合。当然，池化层可能会丢失某些有用的信息，并且对噪声敏感。

4.4、填充、步长和多通道问题

????????Padding：与卷积层类似，用于控制输出大小。例如，在池化层后使用全连接层时，可以使用填充来确保输入和输出大小相同。

????????Stride：池化运算期间每次滑动的窗口的距离。步长越大，窗口在输入图像上的滑动距离就越大，这意味着输出的特征图就越小。步长越小，窗口在输入上的滑动距离就越小，这意味着输出的特征图就越大。

????????多通道： 每个通道上单独池化再拼接；混合池化；全局池化等

4.5、池化层的特点

????????不变性(invariance)： 含平移，旋转和缩放，池化主要指平移不变。

??????? 如果输出是给出图中猫的位置，不管输入怎么移动、缩放，输出相应的改变这就是等变性。

??????? 如果只是输出是否有猫，无论猫怎么移动，输出都保持有猫的判断，就是不变性。

????????

????????不变性(invariance)：池化层主要是平移不变性。

????????保留主要特征的同时减少参数和计算量，防止过拟合。

????????可以帮助网络学习更加抽象的特征。

????????池化层没有参数。

?????????????????

---

4.6、先验视角看卷积和池化

????????

????????卷积：隐藏神经元权重必须与其邻居权重相同。

????????池化：神经元具有少量平移、旋转、缩放的不变性。

????????卷积和池化可以看成是模型引人了很强的先验概率分布。

????????

---

5、LeNet 模型

????????最经典的深度卷积神经网络，由Yann LeCun在1998年提出的LeNet。它是为了解决手写数字识别问题而设计的，并且在当时取得了很好的成功。

LeNet结构

????????????????

• 输入层：LeNet的输入层接受28x28像素的灰度图像。

• 卷积层1：这一层包含6个卷积核，每个卷积核的大小为5x5，卷积步长为1。该层使用Sigmoid激活函数。

• 池化层1：这一层使用2x2的最大池化窗口，步长为2。这一层的作用是降低图像尺寸，并保留最重要的特征。

• 卷积层2：这一层包含16个卷积核，每个卷积核的大小为5x5，卷积步长为1。该层使用Sigmoid激活函数。

• 池化层2：这一层使用2x2的最大池化窗口，步长为2。这一层的作用与池化层1相同。

• 全连接层：这一层包含120个节点，使用Sigmoid激活函数。

• 全连接层：这一层包含84个节点，使用Sigmoid激活函数。

• 输出层：这一层包含10个节点，对应0~9的十个数字。

代码实现：

# 导入必要的库，torchinfo用于查看模型结构
import torch
import torch.nn as nn
from torchinfo import summary

模型定义

# 定义LeNet的网络结构
class LeNet(nn.Module):
    def __init__(self, num_classes=10):
        super(LeNet, self).__init__()
        # 卷积层1：输入1个通道，输出6个通道，卷积核大小为5x5
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        # 卷积层2：输入6个通道，输出16个通道，卷积核大小为5x5
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        # 全连接层1：输入16x4x4=256个节点，输出120个节点，由于输入数据略有差异，修改为16x4x4
        self.fc1 = nn.Linear(in_features=16 * 4 * 4, out_features=120)
        # 全连接层2：输入120个节点，输出84个节点
        self.fc2 = nn.Linear(in_features=120, out_features=84)
        # 输出层：输入84个节点，输出10个节点
        self.fc3 = nn.Linear(in_features=84, out_features=num_classes)

    def forward(self, x):
        # 使用ReLU激活函数，并进行最大池化
        x = torch.relu(self.conv1(x))
        x = nn.functional.max_pool2d(x, kernel_size=2)
        # 使用ReLU激活函数，并进行最大池化
        x = torch.relu(self.conv2(x))
        x = nn.functional.max_pool2d(x, kernel_size=2)
        # 将多维张量展平为一维张量
        x = x.view(-1, 16 * 4 * 4)
        # 全连接层
        x = torch.relu(self.fc1(x))
        # 全连接层
        x = torch.relu(self.fc2(x))
        # 全连接层
        x = self.fc3(x)
        return x

网络结构

# 查看模型结构及参数量，input_size表示示例输入数据的维度信息
summary(LeNet(), input_size=(1, 1, 28, 28))

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
LeNet                                    [1, 10]                   --
├─Conv2d: 1-1                            [1, 6, 24, 24]            156
├─Conv2d: 1-2                            [1, 16, 8, 8]             2,416
├─Linear: 1-3                            [1, 120]                  30,840
├─Linear: 1-4                            [1, 84]                   10,164
├─Linear: 1-5                            [1, 10]                   850
==========================================================================================
Total params: 44,426
Trainable params: 44,426
Non-trainable params: 0
Total mult-adds (M): 0.29
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.04
Params size (MB): 0.18
Estimated Total Size (MB): 0.22
==========================================================================================

模型训练

# 导入必要的库
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
from tqdm import * # tqdm用于显示进度条并评估任务时间开销
import numpy as np
import sys

# 设置随机种子
torch.manual_seed(0)

# 定义模型、优化器、损失函数
model = LeNet()
optimizer = optim.SGD(model.parameters(), lr=0.02)
criterion = nn.CrossEntropyLoss()

# 设置数据变换和数据加载器
transform = transforms.Compose([
    transforms.ToTensor(),  # 将数据转换为张量
])

# 加载训练数据
train_dataset = datasets.MNIST(root='../data/mnist/', train=True, download=True, transform=transform)
# 实例化训练数据加载器
train_loader = DataLoader(train_dataset, batch_size=256, shuffle=True)
# 加载测试数据
test_dataset = datasets.MNIST(root='../data/mnist/', train=False, download=True, transform=transform)
# 实例化测试数据加载器
test_loader = DataLoader(test_dataset, batch_size=256, shuffle=False)

# 设置epoch数并开始训练
num_epochs = 10  # 设置epoch数
loss_history = []  # 创建损失历史记录列表
acc_history = []   # 创建准确率历史记录列表

# tqdm用于显示进度条并评估任务时间开销
for epoch in tqdm(range(num_epochs), file=sys.stdout):
    # 记录损失和预测正确数
    total_loss = 0
    total_correct = 0
    
    # 批量训练
    model.train()
    for inputs, labels in train_loader:

        # 预测、损失函数、反向传播
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        
        # 记录训练集loss
        total_loss += loss.item()
    
    # 测试模型，不计算梯度
    model.eval()
    with torch.no_grad():
        for inputs, labels in test_loader:

            # 预测
            outputs = model(inputs)
            # 记录测试集预测正确数
            total_correct += (outputs.argmax(1) == labels).sum().item()
        
    # 记录训练集损失和测试集准确率
    loss_history.append(np.log10(total_loss))  # 将损失加入损失历史记录列表，由于数值有时较大，这里取对数
    acc_history.append(total_correct / len(test_dataset))# 将准确率加入准确率历史记录列表
    
    # 打印中间值
    if epoch % 2 == 0:
        tqdm.write("Epoch: {0} Loss: {1} Acc: {2}".format(epoch, loss_history[-1], acc_history[-1]))

# 使用Matplotlib绘制损失和准确率的曲线图
import matplotlib.pyplot as plt
plt.plot(loss_history, label='loss')
plt.plot(acc_history, label='accuracy')
plt.legend()
plt.show()

# 输出准确率
print("Accuracy:", acc_history[-1])

Epoch: 0 Loss: 2.7325645021239664 Acc: 0.2633
Epoch: 2 Loss: 2.630008887238046 Acc: 0.6901  
Epoch: 4 Loss: 1.9096679044736495 Acc: 0.9047 
Epoch: 6 Loss: 1.7179356540642037 Acc: 0.9424 
Epoch: 8 Loss: 1.5851480201856594 Acc: 0.9413 
100%|██████████| 10/10 [01:46<00:00, 10.65s/it]

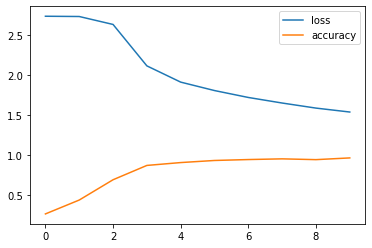
Accuracy: 0.9628

---

参考

7-5 卷积神经网络

Chapter-07/7.6 卷积神经网络代码实现.ipynb · 梗直哥/Deep-Learning-Code - Gitee.com

分组卷积：Grouped convolution-CSDN博客

轻量级网络论文-MobileNetv1 详解 - 知乎