压缩编码之不同缩放参数对重建图像质量的影响的python实现——JPEG变换编码不同压缩率的模拟
原理
JPEG(Joint Photographic Experts Group)是一种常用的图像压缩标准,它通过采用离散余弦变换(DCT)和量化来实现图像的压缩。
离散余弦变换(DCT):
JPEG首先将图像分割成8x8的块。对于每个块,使用离散余弦变换(DCT)将空间域的图像数据转换为频域的系数。
DCT变换会将图像信息从原始的空间域转换到频域,这意味着图像中的信息被表示为一系列频率分量。
量化:
对于DCT变换后的每个8x8块,JPEG使用一个量化矩阵将其系数进行量化。量化的目的是减小高频部分的系数,因为在视觉上,人对于高频细节的敏感性较低。
JPEG定义了不同的量化矩阵,而不同的量化矩阵会导致不同的压缩质量。更高的压缩率通常对应着更大的量化值,因此导致更多的系数被舍弃。
熵编码:
量化后,对每个块的系数进行熵编码,通常使用Huffman编码。
Huffman编码是一种变长编码,通过为频繁出现的值分配短码字,为不太频繁出现的值分配长码字,从而进一步减小图像数据的大小。
压缩率控制:
JPEG允许用户通过设置不同的压缩质量参数来控制压缩率。更高的压缩质量通常对应着更小的压缩率,因为它会导致更少的量化失真。
压缩率的选择通常是一个权衡,用户需要根据具体的应用需求和存储/传输限制来确定适当的压缩率。
总的来说,JPEG通过DCT、量化和熵编码的组合来实现图像的有损压缩。不同的压缩率主要通过调整量化矩阵和压缩质量参数来实现。更高的压缩率通常会导致更多的信息损失,但可以获得更小的文件大小。
python实现下图

提示
结果显示了用不同比例因子去乘标准化阵列后得到的DCT编解码结果。先将原图分割为大小为8×8的子图像,并对每个子图像进行DCT变换,之后对系数阵列进行如下运算来对其量化

最后对量化后的系数阵列进行反变换得到近似图像。
代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena_gray_512.tif",0)
img=img.astype(np.float)
rows,cols=img.shape
img_list = []
img_name_list = []
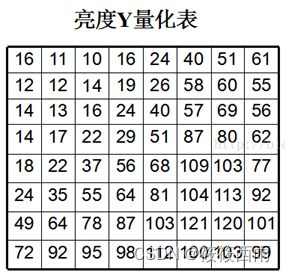
Z = np.array([[16, 11, 10, 16, 24, 40, 51, 61],
[12, 12, 14, 19, 26, 58, 60, 55],
[14, 13, 16, 24, 40, 57, 69, 56],
[14, 17, 22, 29, 51, 87, 80, 62],
[18, 22, 37, 56, 68, 109, 103, 77],
[24, 35, 55, 64, 81, 104, 113, 92],
[49, 64, 78, 87, 103, 121, 120, 101],
[72, 92, 95, 98, 112, 100, 103, 99]])
scl_par=[1,2,4,8,16,32]
for scl in scl_par:
dct_inv_img = np.zeros(img.shape)
for i in range(0, rows, 8):
for j in range(0, cols, 8):
dct = cv2.dct(img[i:i+8, j:j+8])
dct = np.round(dct / (Z * scl))
dct_inv_img[i:i+8, j:j+8] = cv2.idct(dct)
img_list.append(dct_inv_img)
img_name_list.append('scl=' + str(scl))
_, axs = plt.subplots(2, 3)
for i in range(2):
for j in range(3):
axs[i, j].imshow(img_list[i*3+j], cmap='gray')
axs[i, j].set_title(img_name_list[i*3+j])
axs[i, j].axis('off')
plt.show()
结果展示
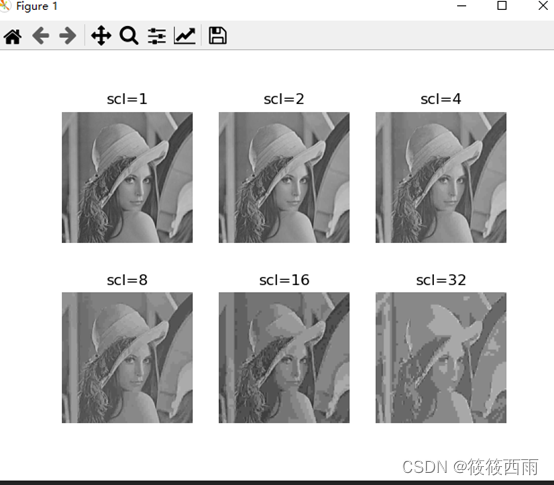
总结
整个JPEG压缩原理就是通过DCT变换去空间冗余来达到图片压缩的。经过DCT变换之后DCT系数只保留的左上角的数据(低频分量数据),右下角部分均变成0.因此,想要进一步压缩就可以从量化表下手。量化表的量化系数越大,得到的量化后的DCT系数就越小,高频信息消失的更多,图片容量就越小。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!