平衡二叉树(AVL树)原理
1、平衡二叉树(AVL树)
平衡二叉树也称之为AVL树,是一个具有以下特征的二叉搜索树:
1、左子树和右子树高度差不会大于1
2、左右两颗子树都满足第一个条件。
1.1、满足条件的AVL树
以下树,左边的高度为3,右边的高度为2,高度差为1,满足条件。
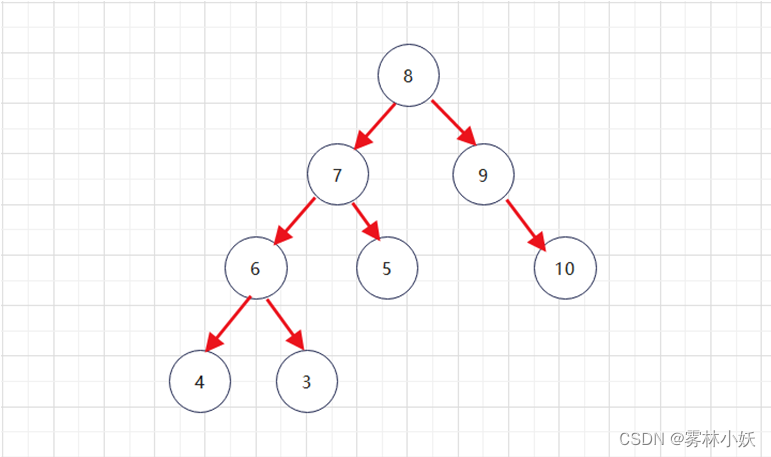
1.2、不满足条件的AVL树
以下树,左边的高度为4,右边的高度为2,高度差大于1,不满足条件。
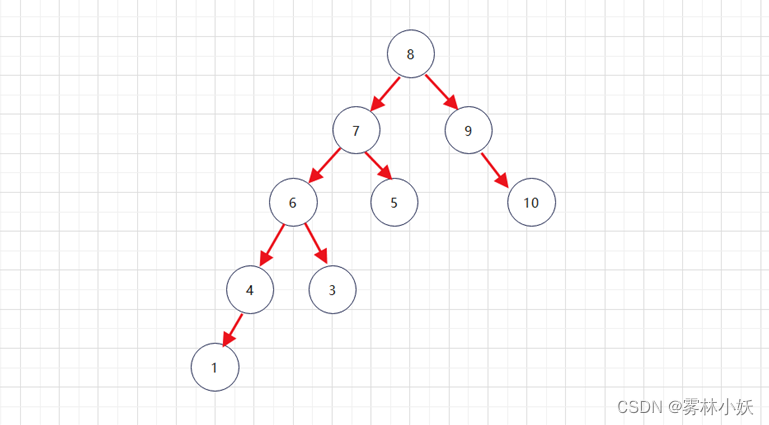
1.3、为什么需要平衡二叉树
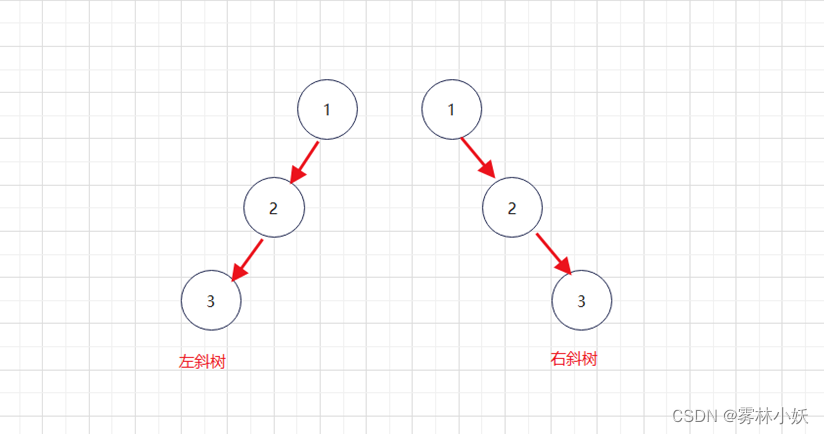
平衡二叉树是为了提高二叉树的查询速度。如果没有平衡二叉树,当我们给有序数据排序时,会产生一颗斜树,斜树是单链结构,失去查询速度快的优势。下面生成一颗斜树。
从图中可以看出,左斜树或者右斜树像是一个链表,插入和删除的速度依旧较快,但是查询的速度较慢,因为遍历深度更深,需要消耗更多的磁盘I/O操作。这个时候我们可以对其进行改造。
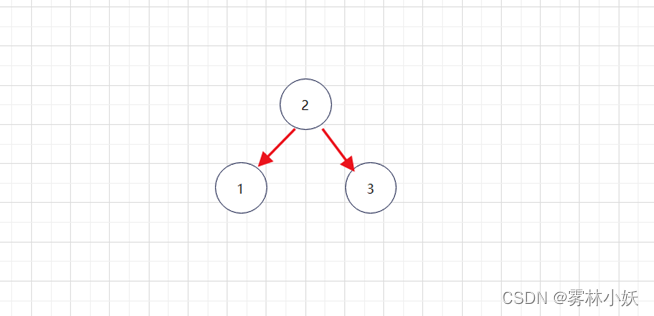
1.4、改造之后的二叉树
这个时候我们可以看出,平衡二叉树有了左子树和右子树,树的高度发生了变化,查询时候的磁盘I/O开销更小,速度更快。
1.5、平衡二叉树需要进行左旋转操作和右旋转操作
平衡二叉树需要满足:左子树和右子树高度差不会大于1,如果大于1这个时候需要进行左旋转或右旋转。如下图二叉树就需要进行左旋转操作。
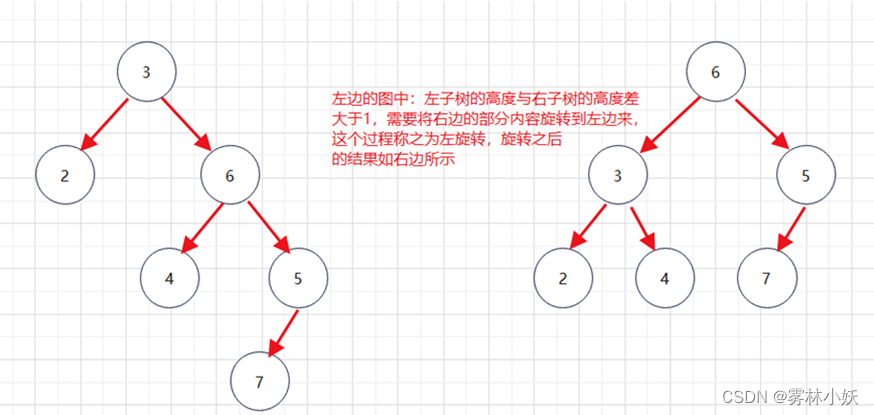
2、平衡二叉树左旋转或右旋转规则
右旋转相反,不做过多的阐述。
2.1、平衡二叉树左旋转
2.1.1、左旋转过程
1、获取当前二叉树的根节点,作为新节点并创建节点
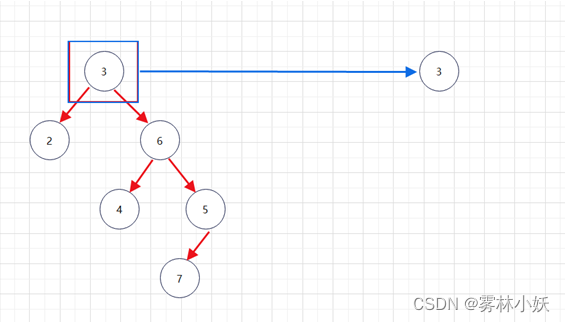
2、获取当前二叉树的左子树,作为新节点的的左子树。
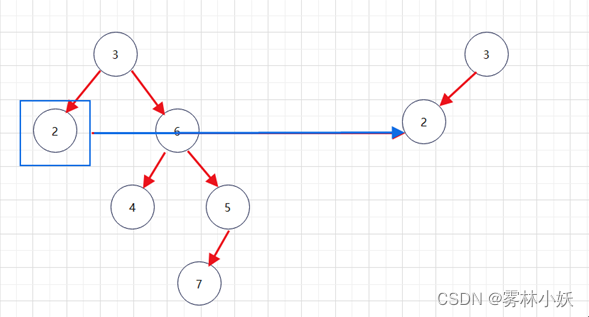
3、获取当前二叉树根节点的右子树的左节点,作为新节点的右子树。
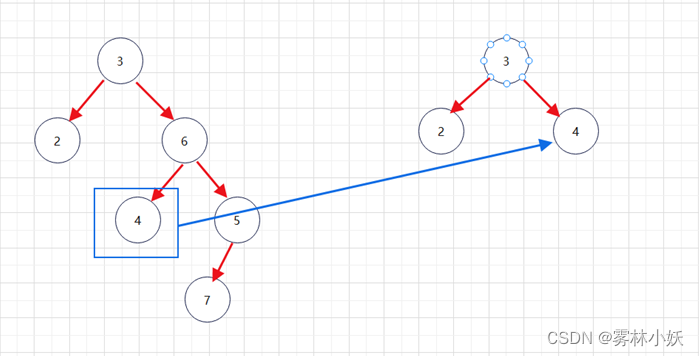
4、获取当前二叉树右节点的值,作为新树的根节点。
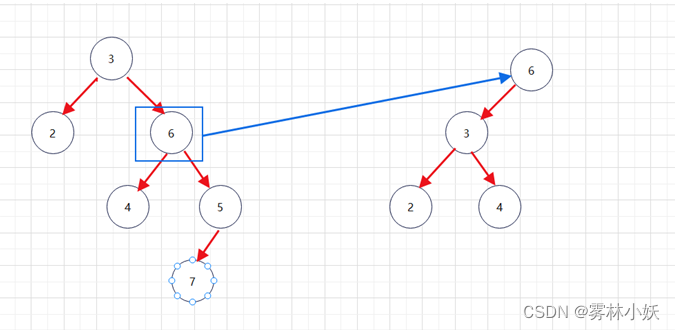
5、获取当前二叉树右节点的右子树,作为新二叉树的右子树
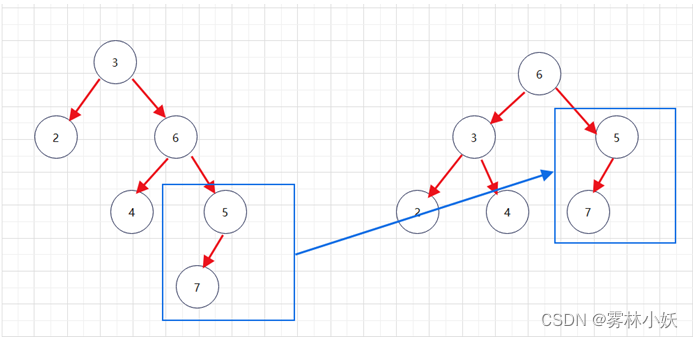
3、平衡二叉树需要双旋转的情况
案例中为了跟上面的案例达到一脉相承的效果,写了一个4.1,比较突兀,就是为了满足条件,大家可以使用权限的数字替代也行。
3.1、双旋转过程
双旋转是基于单旋转(左旋、右旋),其只是对单旋转的代码调用,通过代码来理解双旋转即可。
双旋转代码的核心思想在于:在创建二叉树的过程中,每次添加新的节点,都要判断一下该二叉树是否需要旋转。
如果二叉树需要左旋,则先判断根节点的右子节点的左子树高度是否大于右子树的高度,如果大于则先对根节点的右子树进行右旋,最后再对原二叉树进行左旋;
如果二叉树需要右旋,则先判断根节点的左子节点的右子树高度是否大于左子树的高度,如果大于则先对根节点的左子树进行左旋,最后再对原二叉树进行右旋。
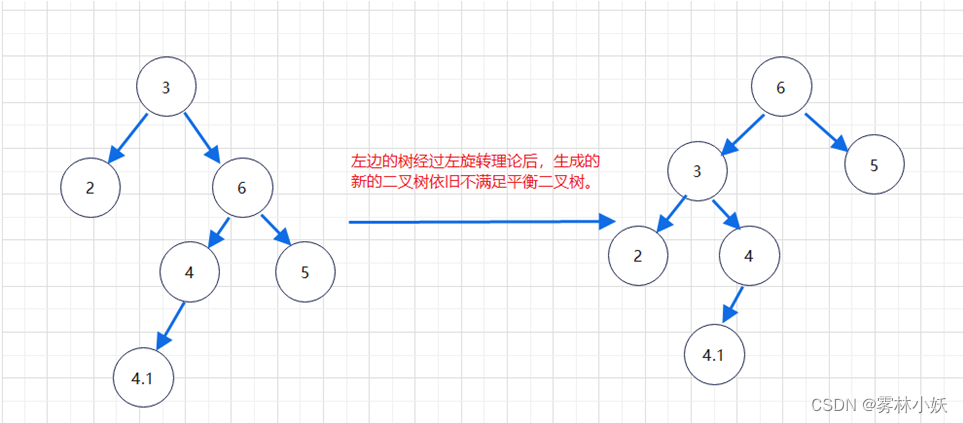
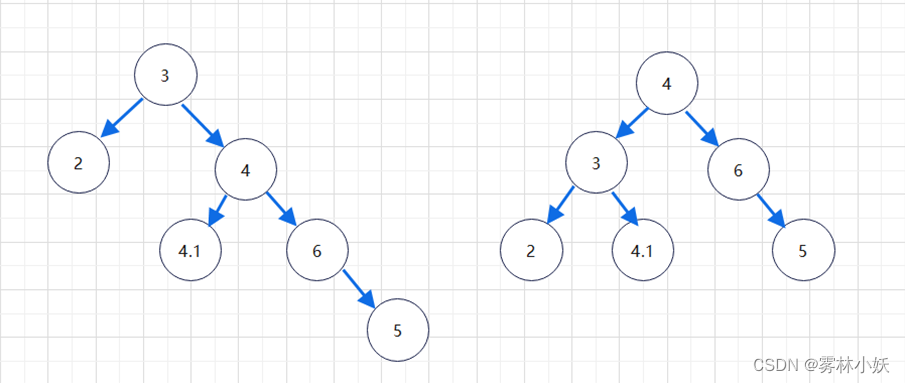
3.2、解决上述问题
我们可以在对原二叉树右旋之前,将其右子树(以 6 为根节点的树)进行一次右旋即可。
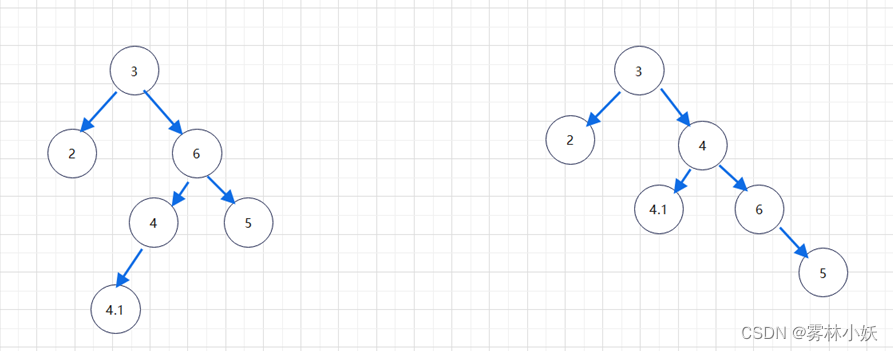
然后再对整颗树进行左旋转
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Spring 框架有哪些缺点?
- 浅谈新一代账务系统的高可用演进思路
- 【HarmonyOS4.0】第九篇-ArkUI布局容器组件(一)
- Linux命令之pwd,cd,ls,cat,more,less,head,tail文件目录类命令的使用
- 游戏开发公司需要具备哪些能力?
- 基于Spring自动注入快速实现策略模式+工厂模式优化过多的if..else
- 一文速通Nginx网关与gateway网关区分
- 【FLIP】一种用于训练CLIP的简单而有效的方案
- HTML 网页设计 简约风格 注册界面
- 司铭宇老师:销售管理技巧培训 如何激发团队斗志