代码随想录算法训练营第十四天| 二叉树 110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和
110. 平衡二叉树
本题与二叉树的高度相关,可以使用后序遍历。

确定函数参数与返回值:由于需要对比左右子树的高度差是否为1,对比的是高度值,因此参数为结点,返回值类型为int。
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
确定终止条件:当为空结点时遍历结束,返回0.
确定递归逻辑:首先先遍历左子树,如果此时返回值为标记-1,没有必要继续遍历了,可以直接返回-1,然后使用if语句判断差值是否为1,如果是的话高度+1.
class Solution {
public:
int getheight(TreeNode* node){
if(node==NULL)return 0;
int leftheight=getheight(node->left);
if (leftheight==-1)return -1;
int rightheight=getheight(node->right);
if(rightheight==-1)return -1;
if(abs(leftheight-rightheight)>1)return -1;
else return 1+max(leftheight,rightheight);
}
bool isBalanced(TreeNode* root) {
return getheight(root)==-1?false:true;
}
};257. 二叉树的所有路径
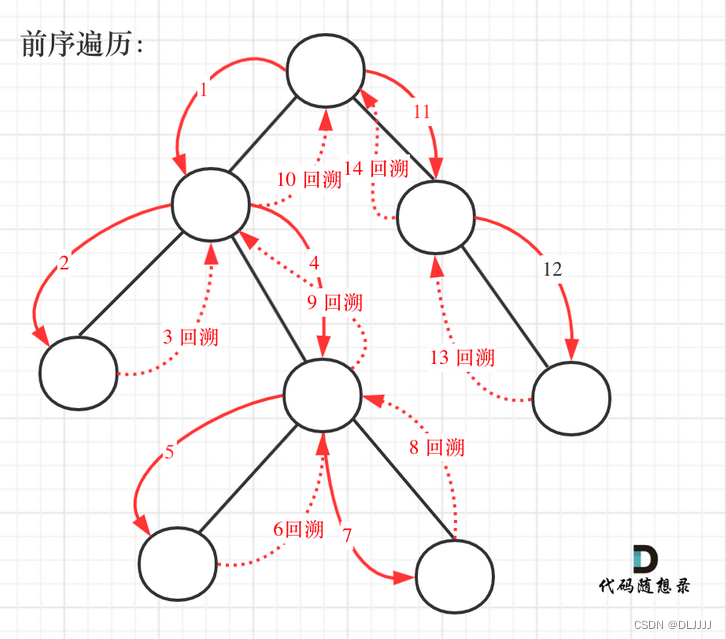
本题想不出回溯的思想,通过查看题解。题解使用前序遍历的思想,因为每次都需要从上往下遍历,使用前序中左右才可以达到。
确定函数参数及返回值:传入根结点,然后需要一个容器保存每条路径,使用一个容器储存结果,由于储存结果都使用引用的方式,可以不需要返回值。
确定函数终止条件:常常会理所当然想到如果遍历到的结点为空,递归返回。但是对于本题来说,找到叶子结点就可以结束递归了,因此设置左右结点都为空时循环停止,然后输出结果,将前面的路径转化为字符串导出。
代码中,由于到最后一个结点就结束了,如果不把path.push_back()放其前面的话,path会无法访问到叶子结点。
确定单层函数逻辑:由于前面没有确定是否是空结点,因此这里需要判断左节点以及右节点是否为空,如果为空则不需要放入路径中。由于此时递归回到叶子结点才结束,为了返回到上一个结点(回溯),需要把最后的弹出。
出现错误
在函数定义中,忘记使用引用,导致一直输出空结果。
class Solution {
public:
void travelsal(TreeNode* node,vector<int> &path,vector<string>&res){
path.push_back(node->val);//中,为了使最后一个结点(叶子结点)也要放入数组中
if(node->left==NULL&&node->right==NULL){
string spath;
for(int i=0;i<path.size()-1;i++){
spath+=to_string(path[i]);
spath+="->";
}
spath += to_string(path[path.size() - 1]);
res.push_back(spath);
return;
}
if(node->left){
travelsal(node->left,path,res);
path.pop_back();
}
if(node->right){
travelsal(node->right,path,res);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
vector<int>path;
if(root==NULL) return res;
travelsal(root,path,res);
return res;
}
};404. 左叶子之和
本题需要使用后序遍历。本题有一个地方没有想清楚就去看了题解,就是:判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
确定函数参数以及返回值类型:返回值需要为int,函数参数为结点
确定终止条件:当结点没有左子结点时,就没有必要继续进行下去了。
确定单层循环逻辑:由于叶子结点无法判断是否为子结点,需要判断它的上一个结点,如果上一个结点满足有左子结点,然后左子节点是叶子结点,则结束,记录它的左子结点的值。然后对于往右遍历的,由于那个if判断,所以valright也会是其左子结点的值。
class Solution {
public:
int valLeftLeaves(TreeNode* node){
if(node->left==NULL)return 0;
// if(node->left&&node->right) return 0;
int valleft=valLeftLeaves(node->left);
if(node->left && !node->left->left&&!node->left->right) valleft=node->left->val;
cout<<valleft<<" ";
//************************************************
int valright=valLeftLeaves(node->right);//卡在这里其实最后只要算的是left值,可以进行往右遍历,通过上面一个if条件确保提取的是左叶子结点
int sum=valleft+valright;
return sum;
}
int sumOfLeftLeaves(TreeNode* root) {
return valLeftLeaves(root);
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第十章 web入门
- 【Image captioning】图像描述标注(Image captioning)软件的设计与实现
- Kasada p.js (kpsdk-cd、integrity)
- 读取小数部分
- 干货:教你如何在JMeter中调用Python代码N种方法!
- WEB服务器-Tomcat
- 基于xgboost-LGBM-SVM的病人哮喘病识别检测 数据+代码
- Python爬虫基础篇1
- 【粉丝福利社】巧用ChatGPT高效搞定Excel数据分析(文末送书-进行中)
- 生产系统稳定上线600天!中国联通CUDB for OceanBase的开源共建和规模化应用