前缀和数组、差分数组、树状数组在Leetcode中的应用
文章目录
前缀和数组、差分数组、树状数组知识简单回顾
之前的文章中讲了前缀和数组、差分数组和树状数组。主要总结一下:
原数组: a i a_i ai?
前缀和数组: S i = a 1 + a 2 + . . . + a i S_i = a_1 + a_2 + ... + a_i Si?=a1?+a2?+...+ai?
差分数组: X i = a i ? a i ? 1 X_i = a_i - a_{i - 1} Xi?=ai??ai?1?
树状数组:前缀和数组的一种特殊表现形式,使得前缀和数组更方便进行单点修改。
关系:原数组是前缀和数组的差分数组;原数组是差分数组的前缀和数组。
前缀和数组与差分数组、树状数组并没有增加信息,只是原数组信息的另外一种表示,在处理问题时数据的处理时间复杂度不同。
问题1:求原数组的区间和,原数组上的时间复杂度为 O ( n ) O(n) O(n),前缀和数组上操作时间复杂度为 O ( 1 ) O(1) O(1).
问题2:原数组区间元素修改(同时加一个值)
例如a2到a5的元素都增加d, 体现在差分数组上为x2+d, x6 - d, 其他元素不变。即只有两个点发生变化。
上面两类问题下原数组时间复杂度为 O ( n ) O(n) O(n), 差分数组或前缀和数组上的时间复杂度为 O ( 1 ) O(1) O(1).
Leetcode 1109. 航班预订统计
题目描述:

题目分析:相当于对于原数组,某一个区间上的值同时增加一个数。即区间修改。这种情况下用差分数组更方便。例如a2到a5的元素都增加d, 体现在差分数组上为x2 + d, x6 - d, 其他元素不变。即只有两个点发生变化。
所以本题先根据输入,对差分数组进行单点修改(相当于对原数组进行区间修改),最后再对差分数组求前缀和,即得到了原数组。
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> d(n + 1); //原数组的差分数组
for (int i = 0; i < bookings.size(); i++) {
int start = bookings[i][0];
int last = bookings[i][1];
int seat = bookings[i][2];
d[start] += seat;
if (last + 1 <= n) d[last + 1] -= seat;
}
// for (int i = 1; i <= n; i++) printf("%d ", d[i]);
// printf("\n");
// printf("s finish\n");
vector<int> res(n); //res[i]代表原数组的第i + 1位的值
res[0] = d[1]; //原数组为a, res[i] = a[i + 1]
for (int i = 2; i <= n; i++) {
// 原数组: a[i] = a[i - 1] + d[i];
//res原数组是原数组的位移: res[i] = a[i + 1]
res[i - 1] = res[i - 2] + d[i];
}
return res;
}
};
代码运行结果:

总结:本题直接用差分数组,求前缀和即得到原数组。这里求前缀和可以直接求,也可以利用树状数组来求。
本题也可以在区间修改的过程中,直接利用树状数组来维护原数组:
#define lowbit(x) (x & (-x))
class FenwickTree{
public:
FenwickTree(int size): n(size), c(size + 1){}
//size表示最大访问到的下标,所以c数组的长度就是size + 1;
void add(int i, int x) {
//单点修改:在原数组的第i个位置上的元素加x
while(i <= n) {
c[i] = c[i] + x;
i = i + lowbit(i);
}
return;
}
int query(int x) {
//对原数组的前x位进行前缀和查询
int sum = 0;
while (x) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int at(int ind) {
//原数组在ind位置的值
return query(ind) - query(ind - 1);
}
void output() {
int len = 0;
for (int i = 1; i <= n; i++) {
len += printf("%5d", i);
}
printf("\n");
for (int i = 1; i <= len + 6; i++) printf("=");
printf("\n");
for (int i = 1; i <= n; i++) {
printf("%5d", c[i]);
}
printf("\n");
for (int i = 1; i <= n; i++) printf("%5d", query(i) - query(i - 1));
printf("\n\n\n");
return;
}
private:
int n; //树状数组所维护的下标的最大上限
vector <int> c; //树状数组
};
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
FenwickTree tree(n);
for (auto x: bookings) {
tree.add(x[0], x[2]);
tree.add(x[1] + 1, -x[2]);
}
vector<int> res(n);
for (int i = 0; i < n; i++) {
res[i] = tree.query(i + 1);
}
return res;
}
};
上述代码相当于把差分数组看做原数组,对差分数组单点修改,然后这个过程中直接利用树状数组维护其前缀和数组。最后输出差分数组的树状数组。
Leetcode 307. 区域和检索-数组可修改

题目分析:同时涉及到原数组的单点修改和区间和查询,如果存储原数组求区间和的时候复杂度为O(n), 如果存储前缀和数组单点修改的时候复杂度为O(n), 所以可以直接存储树状数组,无论单点修改还是求区间和,复杂度均为O(logn)。
需要注意前缀和数组我们实现的时候下标是从1开始的,需要和本题中的数组有一个下标偏移转换。
#define lowbit(x) (x & (-x))
class FenwickTree{
public:
FenwickTree(int size): n(size), c(size + 1){}
//size表示最大访问到的下标,所以c数组的长度就是size + 1;
void add(int i, int x) {
//单点修改:在原数组的第i个位置上的元素加x
while(i <= n) {
c[i] = c[i] + x;
i = i + lowbit(i);
}
return;
}
int query(int x) {
//对原数组的前x位进行前缀和查询
int sum = 0;
while (x) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int at(int ind) {
//原数组在ind位置的值
return query(ind) - query(ind - 1);
}
void output() {
int len = 0;
for (int i = 1; i <= n; i++) {
len += printf("%5d", i);
}
printf("\n");
for (int i = 1; i <= len + 6; i++) printf("=");
printf("\n");
for (int i = 1; i <= n; i++) {
printf("%5d", c[i]);
}
printf("\n");
for (int i = 1; i <= n; i++) printf("%5d", query(i) - query(i - 1));
printf("\n\n\n");
return;
}
private:
int n; //树状数组所维护的下标的最大上限
vector <int> c; //树状数组
};
class NumArray {
public:
FenwickTree tree;
NumArray(vector<int>& nums):tree(nums.size()) {
int n = nums.size();
// printf("n : %d\n", n);
for (int i = 0; i < n; i++) {
tree.add(i + 1, nums[i]);
// num的 i 索引 ~ tree的 i+1 索引
}
}
void update(int index, int val) {
tree.add(index + 1, val - tree.at(index + 1));
return;
}
int sumRange(int left, int right) {
return tree.query(right + 1) - tree.query(left - 1 + 1);
}
// private:
// FenwickTree tree;
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* obj->update(index,val);
* int param_2 = obj->sumRange(left,right);
*/
总结:树状数组最直接的应用。
LeetCode 面试题10.10. 数字流的秩

题目分析:一开始看到找到小于等于x的个数,先想到的是二叉排序树,同时维护一个二叉排序树,以及每个节点所包含的节点个数。但是二叉排序树又有一个弊端,就是当读入数字有序的时候,会退化为一个链表。这时候就又要用到AVL数,甚至红黑树,问题变得复杂。
看到本题的数字范围,x <= 50000, 不是很大,事实上本题的数字范围还是>=0的。所以可以用计数数组来建模(计数排序时有用到计数数组)。
首先建立一个计数数组a[n],下标最大范围为50000. 然后读入一个数字x时,只需让a[x]+=1;
当要求某个数字x,有多少个数字小于等于它时,实际上就是求a[n]数组中x位置对应的前缀和。
所以本题实际上就是只涉及计数数组的单点修改和前缀和查询。 而为了更快速的求前缀和,我们可以用树状数组来实现。
#define lowbit(x) (x & (-x))
class FenwickTree{
public:
FenwickTree(int size): n(size), c(size + 1){}
//size表示最大访问到的下标,所以c数组的长度就是size + 1;
void add(int i, int x) {
//单点修改:在原数组的第i个位置上的元素加x
while(i <= n) {
c[i] = c[i] + x;
i = i + lowbit(i);
}
return;
}
int query(int x) {
//对原数组的前x位进行前缀和查询
int sum = 0;
while (x) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int at(int ind) {
//原数组在ind位置的值
return query(ind) - query(ind - 1);
}
void output() {
int len = 0;
for (int i = 1; i <= n; i++) {
len += printf("%5d", i);
}
printf("\n");
for (int i = 1; i <= len + 6; i++) printf("=");
printf("\n");
for (int i = 1; i <= n; i++) {
printf("%5d", c[i]);
}
printf("\n");
for (int i = 1; i <= n; i++) printf("%5d", query(i) - query(i - 1));
printf("\n\n\n");
return;
}
private:
int n; //树状数组所维护的下标的最大上限
vector <int> c; //树状数组
};
class StreamRank {
public:
FenwickTree tree;
StreamRank():tree(50001) {
// tree的索引i+1 ~ 数字i
// tree为计数数组
}
void track(int x) {
tree.add(x + 1, 1);
return;
}
int getRankOfNumber(int x) {
return tree.query(x + 1);
}
};
/**
* Your StreamRank object will be instantiated and called as such:
* StreamRank* obj = new StreamRank();
* obj->track(x);
* int param_2 = obj->getRankOfNumber(x);
*/
提交结果:

总结:需要先分析题目,如何建模解决问题。然后再建模解模的过程中,为了快速求解其中的前缀和,我们用到了树状数组。
LeetCode 1310. 子数组异或查询

题目分析:本题求的是区间所有元素的异或。我们已经知道区间所有元素的和,可以用前缀和的差来求。因为和的逆运算就是减法。那么仿照前缀和的思路,区间和的异或运算,我们也可以采用关于前缀和的异或来求。
这里就涉及到异或运算的的一个性质,那就是它的逆运算还是它自己。
比如对于加减法, a + b = c a+b = c a+b=c, 因为减法是加法的逆运算,所以用减法,可以由c和a运算得到 b . ( c ? a = b ) b. (c - a = b) b.(c?a=b), 或者由c和b运算得到 a . ( c ? b = a ) a. (c - b = a) a.(c?b=a);
对于异或运算, 如果已知a ^ b = c, 那么如何由a和c运算得到b呢?答案就是异或运算,即c ^ a = b, 同样 c ^ b = a。
所以对于本题,完全可以建立一个异或运算的前缀和数组,对于区间和,用两个端点的异或前缀和再做异或运算,即可解决。
class Solution {
public:
vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) {
int n = arr.size();
int m = queries.size();
vector<int> sum_xor(n); //异或的前缀和数组
vector<int> res(m);
for (int i = 0; i < n; i++) {
if (i == 0) sum_xor[i] = arr[i];
else sum_xor[i] = sum_xor[i - 1] ^ arr[i];
}
for (int i = 0; i < m; i++) {
int start = queries[i][0];
int end = queries[i][1];
if (start == 0) res[i] = sum_xor[end];
else res[i] = sum_xor[end] ^ sum_xor[start - 1];
}
return res;
}
};

总结:用前缀和的思路,需要了解异或运算的一个性质,其逆运算仍为自己。
LeetCode 1409. 查询带键的排列

题目分析:本题比较复杂的是需要多次移动数组P中的元素。不论是直接存储维护原数组还是用哈希表,每次移动的时间复杂度都是O(n)。
所以这里考虑使用一个下标处理小技巧,即使用计数数组。将P数组中的数字存储在计数数组中:
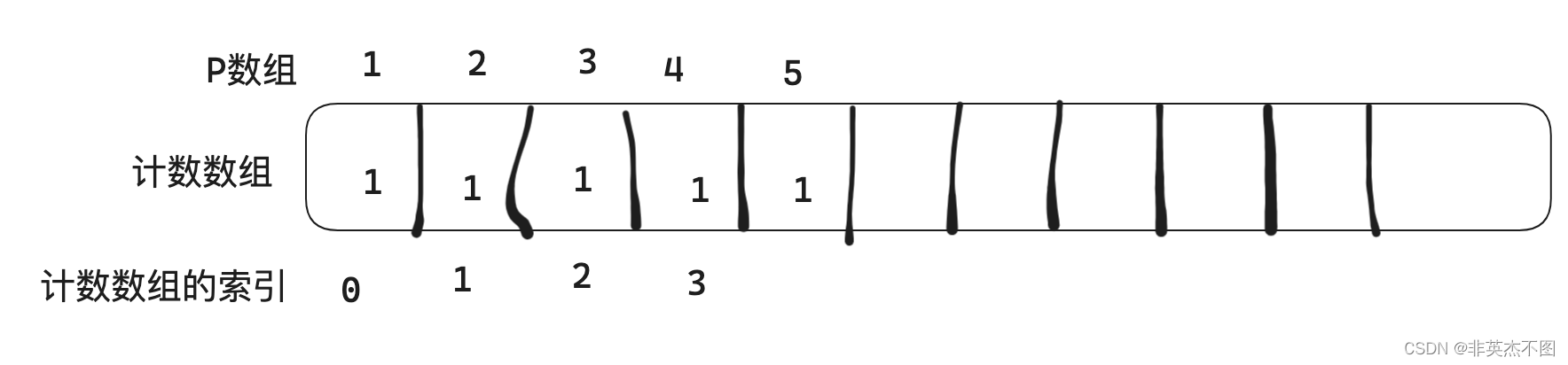
例如P数组中的数字3对应计数数组的前缀和是3,就说明3这个数字在P数组中是第三个数(对应P数组的索引)。
然后本题需要将P数组中特定位置的数字移动到最前面,所以可以对计数数组做一定量的向右偏移,移动的过程就可以这样操作:

这样通过计算计数数组的前缀和,就可以快速的求出P数组对应元素的索引。 移动的过程也仅仅是计数数组的单点修改。
所以本题主要维护一个计数数组,再维护数组P中的每一个数在计数数组中的索引,即可解决题目要求。
#define lowbit(x) (x & (-x))
class FenwickTree{
public:
FenwickTree(int size): n(size), c(size + 1){}
//size表示最大访问到的下标,所以c数组的长度就是size + 1;
void add(int i, int x) {
//单点修改:在原数组的第i个位置上的元素加x
while(i <= n) {
c[i] = c[i] + x;
i = i + lowbit(i);
}
return;
}
int query(int x) {
//对原数组的前x位进行前缀和查询
int sum = 0;
while (x) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int at(int ind) {
//原数组在ind位置的值
return query(ind) - query(ind - 1);
}
void output() {
int len = 0;
for (int i = 1; i <= n; i++) {
len += printf("%5d", i);
}
printf("\n");
for (int i = 1; i <= len + 6; i++) printf("=");
printf("\n");
for (int i = 1; i <= n; i++) {
printf("%5d", c[i]);
}
printf("\n");
for (int i = 1; i <= n; i++) printf("%5d", query(i) - query(i - 1));
printf("\n\n\n");
return;
}
private:
int n; //树状数组所维护的下标的最大上限
vector <int> c; //树状数组
};
class Solution {
public:
vector<int> processQueries(vector<int>& queries, int m) {
//计数数组数组a(对应树状数组tree):0~2m+5, 初始时m~2m的位置存储1, 其前缀和即为P数组对应的索引。
//索引数组arr_ind: 存储排列P在计数数组中的存放位置,初始时0-m分别存储m~2m
FenwickTree tree(2 * m + 5); //大数组,计数数组对应的树状数组
vector<int> arr_ind(m + 1);
for (int i = 1; i <= m; i++) {
tree.add(m + i, 1); //计数数组先完成初始化计数
arr_ind[i] = m + i;
}
int n = queries.size();
vector<int> ret(n);
int prefix_ind = m;
for (int i = 0; i < n; i++) {
int num = queries[i];
int ind_a = arr_ind[num];
int ind_p = tree.query(ind_a) - 1; //通过计数数组的前缀和求出P数组的索引
ret[i] = ind_p;
//将num这个数字移动到了原数组a的prefix_ind位置上,其余不变
tree.add(prefix_ind, 1);
tree.add(ind_a, -1);
arr_ind[num] = prefix_ind;
prefix_ind--;
}
return ret;
}
};
提交结果:
总结:本题通过维护计数数组,既可以快速求出原数组P的索引,也可以通过单点修改就实现数字的移动。思路巧妙,相关技巧可供参考。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!