【AI数学】NeRF中的球面谐波函数（Spherical Harmonics）
球面谐波（SH）因为其良好的性质活跃在NeRF、Plenoxels、3DGS等显隐式场景表示的方法中。
问：球面谐波是什么？
答：一组基函数。可以理解为傅里叶分解的一种特殊形式，即“任何函数都可以用这组基的算术组合来近似”。
先描述一种通用情况：
假设我们有一组基数为3的完备基函数：
[
e
1
(
x
)
,
e
2
(
x
)
,
e
3
(
x
)
]
[e_1(x), e_2(x),e_3(x)]
[e1?(x),e2?(x),e3?(x)]
我们存在一个目标函数
f
(
x
)
f(x)
f(x)，那么
f
(
x
)
f(x)
f(x)可以用这组基函数来表达：
f
(
x
)
=
a
1
e
1
(
x
)
+
a
2
e
2
(
x
)
+
a
3
e
3
(
x
)
f(x)=a_1e_1(x)+a_2e_2(x)+a_3e_3(x)
f(x)=a1?e1?(x)+a2?e2?(x)+a3?e3?(x)这里的
[
a
1
,
a
2
,
a
3
]
[a_1,a_2,a_3]
[a1?,a2?,a3?]就是这组基的系数了。当然，我们可以用更“细致”的正交基来拟合目标函数，一般对应着更多的基数。我们可以浅看一张图：
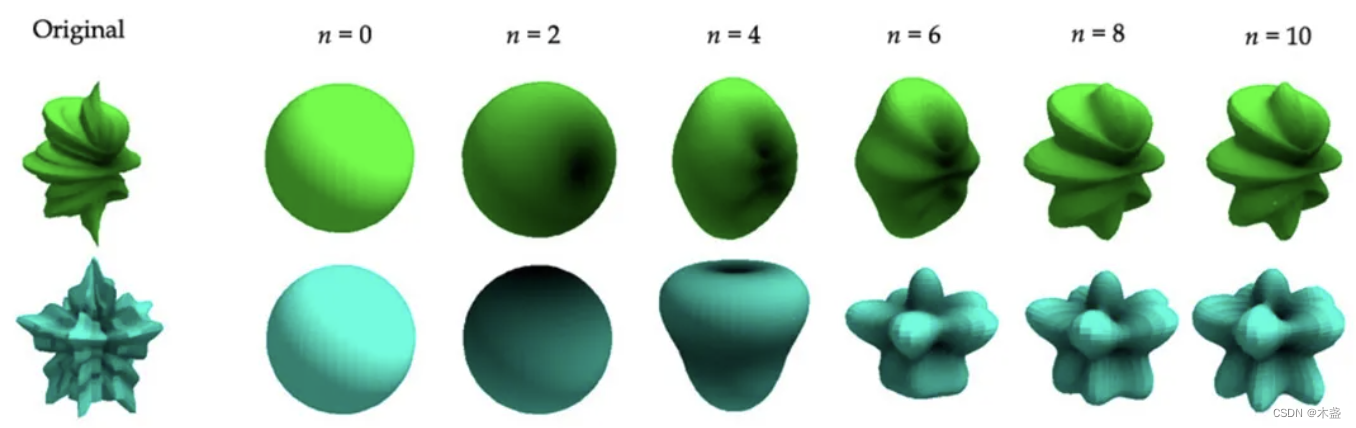
这里的n表示基数，用的是球面谐波基。由此可见，基数越多，拟合效果越佳。
球面谐波
球面谐波基，顾名思义，跟球面有关。首次将SH引入NeRF的工作是PlenOctrees。
未完待续…
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！