代码随想录刷题题Day33

刷题的第三十三天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day33 任务
● 139.单词拆分
● 关于多重背包，你该了解这些！
● 背包问题总结篇！

1 单词拆分

139.单词拆分

思路：
动态规划法
（1）确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词
（2）递推公式

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
（3）dp数组如何初始化

dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递推的根基，dp[0]一定要为true，否则递推下去后面都都是false了

（4）确定遍历顺序

（1）如果求组合数就是外层for循环遍历物品，内层for遍历背包。
（2）如果求排列数就是外层for遍历背包，内层for循环遍历物品。

本题是求排列数
（5）举例推导dp[i]

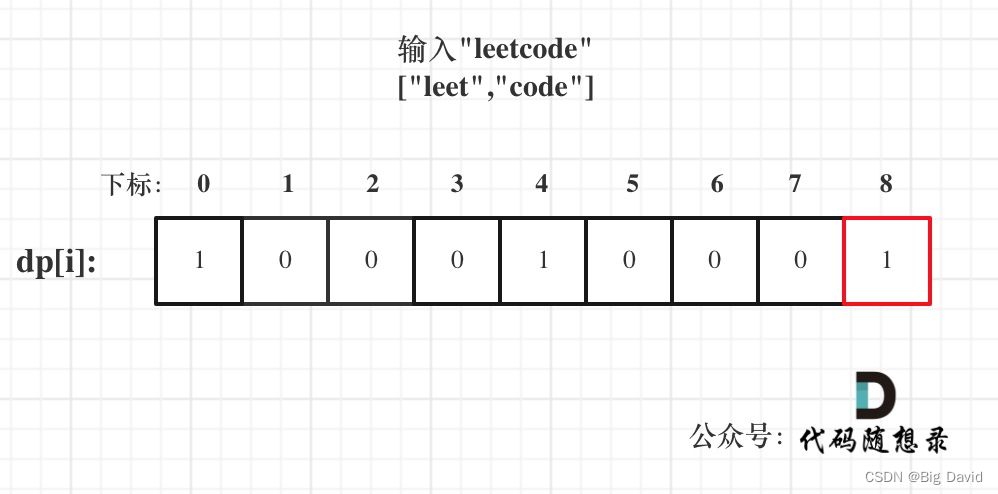
C++：

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;
        for (int i = 1; i <= s.size(); i++) {// 遍历背包
            for (int j = 0; j < i; j++) { // 遍历物品
                string word = s.substr(j, i - j);
                if (wordSet.find(word) != wordSet.end() && dp[j]) {//substr(起始位置，截取的个数)
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

时间复杂度：$O(n^3)$，因为substr返回子串的副本是$O(n)$的复杂度
空间复杂度：$O(n)$

2 多重背包

有N种物品和一个容量为V的背包。第i种物品最多有$M_i$件可用，每件耗费的空间是$C_i$ ，价值是$W_i$ 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。
多重背包和01背包很像。


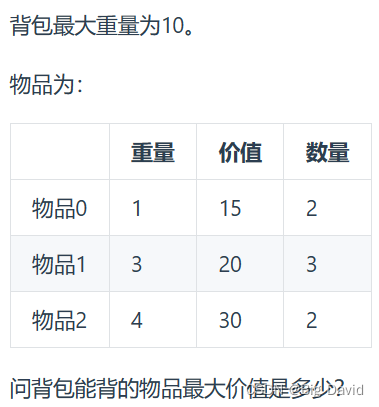
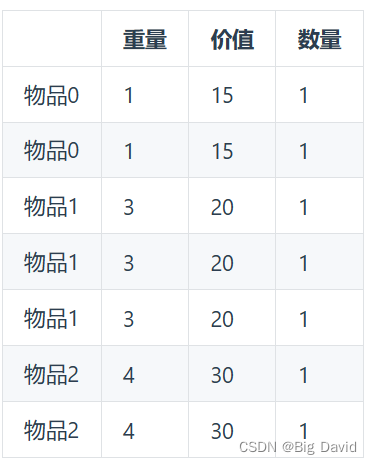
C++：

#include <iostream>
#include <vector>
using namespace std;
int main()
{
	int bagWeight, n;
	cin >> bagWeight >> n;
	vector<int> weight(n, 0);
	vector<int> value(n, 0);
	vector<int> nums(n, 0);
	for (int i = 0; i < n; i++) cin >> weight[i];
	for (int i = 0; i < n; i++) cin >> value[i];
	for (int i = 0; i < n; i++) cin >> nums[i];

	vector<int> dp(bagWeight + 1, 0);
	for(int i = 0; i < n; i++) { // 遍历物品
		for (int j = bagWeight; j > weight[i]; j--) { // 背包
			for (int k = 1; k <= nums[i] && (j - k * weight[i] >= 0; k++) {// 遍历个数
				dp[j] = max(dp[j], dp[j - k * weight[i] + k * value[i]);
			}
		}
	}
	cout << dp[bagWeight] << endl;
}

时间复杂度：$O(m\times n\times k)$，m：物品种类个数，n背包容量，k单类物品数量

3 背包问题总结

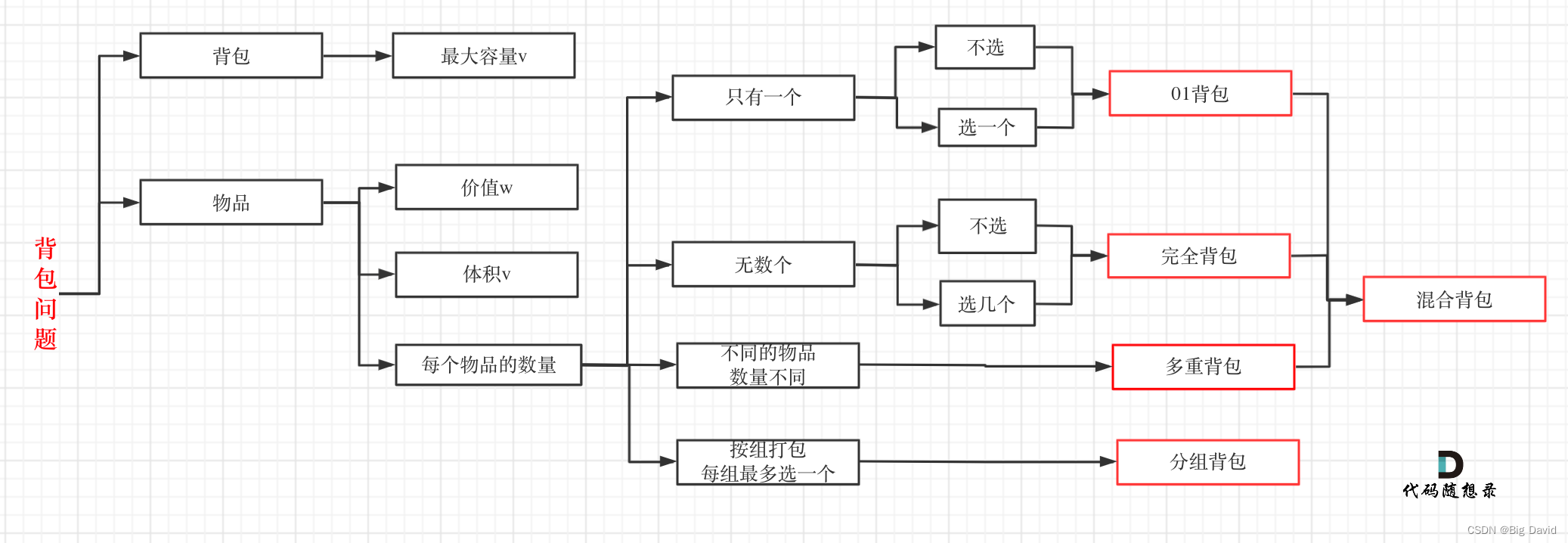
五部曲：
（1）确定dp数组（dp table）以及下标的含义
（2）确定递推公式
（3）dp数组如何初始化
（4）确定遍历顺序
（5）举例推导dp数组

确定递推公式和确定遍历顺序都具有规律性和代表性

3.1 背包递推公式

1. 问能否能装满背包（或者最多装多少）$d[j]=max(dp[j],dp[j?nums[i]]+nums[i])$
2. 问装满背包有几种方法：$dp[j]+=dp[j?nums[i]]$
3. 问背包装满最大价值：$dp[j]=max(dp[j],dp[j?weight[i]]+value[i]);$
4. 问装满背包所有物品的最小个数：$dp[j]=min(dp[j?coins[i]]+1,dp[j])$

3.2 遍历顺序

01背包：
（1）二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历
（2）一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历

完全背包：
纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历

（1）如果求组合数就是外层for循环遍历物品，内层for遍历背包。
（2）如果求排列数就是外层for遍历背包，内层for循环遍历物品。

---

鼓励坚持三十四天的自己😀😀😀