python解决求解图的最短路径问题

对于图的经常遇到的问题当中，还有一个经典问题，那就是关于如何求解图的最短路径问题，主要是求某一顶点到其余各个顶点之间的最短路径问题，这也称为是一对多的最短路径问题，这个问题的阶梯思路一般使用的是迪杰斯特拉算法来解决。

对于给定的graph二维列表和point列表，这两个分别用于表示一个有向连通图各顶点之间的距离和各顶点的名称，对这个两个列表所表示的有向连通图求某一个顶点到其余各个顶点之间的最短路径，并且需要将到各个顶点之间的路径体现出来。

如下例子：

添加图片注释，不超过 140 字（可选）

添加图片注释，不超过 140 字（可选）

以上例子的输出为：

添加图片注释，不超过 140 字（可选）

另一个例子如下：

添加图片注释，不超过 140 字（可选）

对应的输出为：

添加图片注释，不超过 140 字（可选）

针对该问题的解决思路，将会使用到迪杰斯特拉算法思想来解决，该算法主要是用于求解某一个顶点到其余各个顶点的最短路径，基本步骤是，给定某一个顶点start来作为起点，定义使用集合use来表示已经找到的最短路径的顶点的集合，定义使用集合unuse来表示还未找到最短路径的顶点的集合，初始的时候，集合已经找到最短路径use中只有定义的起点use，unuse集合中则包含除了start之外的其他所有顶点，使用length列表来表示当前顶点start到其余各个顶点的最短路径，如果起点与某一个顶点之间是没有路径的，则使用sys.maxsize来表示，定义front来表示起点到达各个顶点的上一个顶点。

从length列表中来选取最短路径，说今年已经找到了顶点到达该顶点的最短路径，并且将该顶点加入到use集合中，同时从unuse集合中移除出去。如果起点到某一个顶点之间的距离会大于起点到该顶点之间的一个顶点距离加上中间顶点到该顶点之间的距离，则表示length列表当中的值不是最短距离，需要将length中的该值进行更新并且front列表也进行更新。将前两个步骤进行重复，直到use集合当中包含了所有的顶点则结束。

对于如上的步骤使用一个图来进行整个流程的解释：

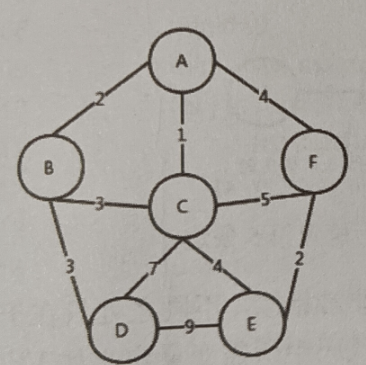
添加图片注释，不超过 140 字（可选）

首先是对于length列表中现挑选出最短的边是3，也就是顶点D和顶点B之间的距离，将集合use[1]置为1，同时将length列表和front列表进行更新，由于顶点B的加入，顶点D到顶点A的距离变成了5，到定点C的距离变成了6，并且定点A和顶点C的上一个顶点变成了B，如下图所示：

添加图片注释，不超过 140 字（可选）

然后就是在length列表中继续挑选，选出了最短的边是5，是为顶点D到定点A之间的距离，更新use[0]=1，更新length和front列表，A的加入会导致定点F到定点A之间的距离变成了9，定点F的上一个顶点变成了A，如下图所示：

添加图片注释，不超过 140 字（可选）

继续挑选出length列表中的对应的use的值为0的最短边，也即是顶点B到顶点C之间的边的，use[2]=1,C虽然加入，但是不需要更新length和front列表。

添加图片注释，不超过 140 字（可选）

继续就是顶点D到顶点E之间的边是use的值为0的边，更新use[4]=1，无需更新length和front。

最后就是顶点A到定点F之间的边，当F顶点加入之后，也就已经求出了最短路径：

添加图片注释，不超过 140 字（可选）

使用python实现的代码如下：

import sys
def dijkstra(graph,point,start):
    length=graph[start]
    use=[0 for _ in range(len(graph))]
    use[start]=1
    front=[point[start] for _ in range(len(graph))]
    for i in range(len(graph)):
        minid=0
        min_=sys.maxsize
        for j in range(len(length)):
            if not use[j] and length[j]<min_:
                min_=length[j]
                minid=j
        use[minid]=1
        for k in range(len(graph)):
            if not use[k] and min_+graph[minid][k]<length[k]:
                length[k]=min_+graph[minid][k]
                front[k]=point[minid]    
    return length,front