欧拉图及其应用
什么是欧拉图
提到欧拉图就要谈到哥尼斯堡七桥问题,最初有这样的一个问题的:18世纪中叶,东普鲁士哥尼斯堡城有一条贯穿全城的普雷格尔河,河中有两个岛,通过七座桥彼此相连,如下图所示
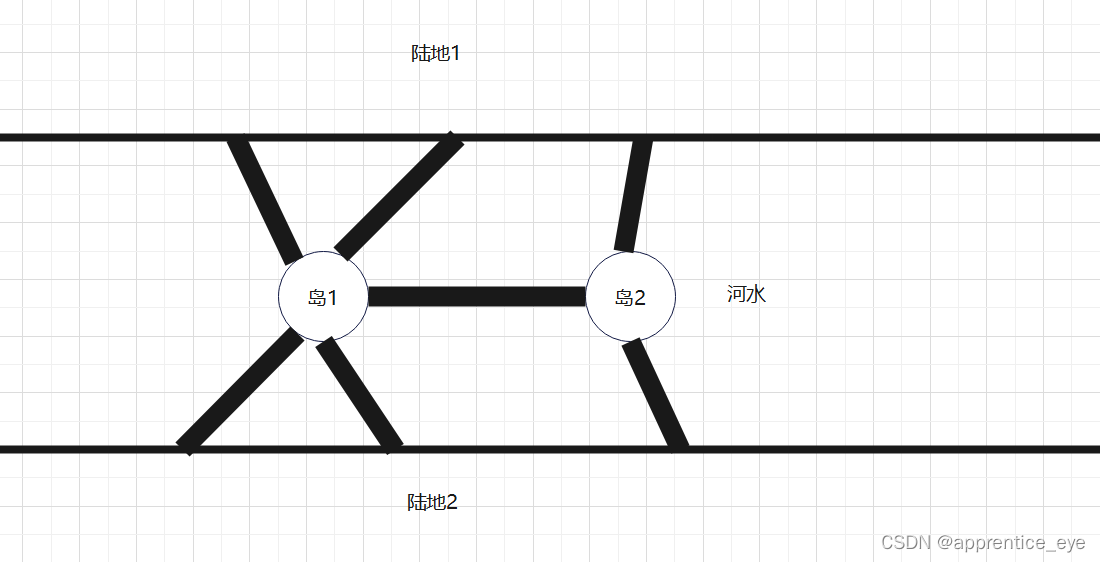
问题是这样的:有人从四块陆地中的任意一块出发,按什么样的路线能做到每座桥只通过一次而最后返回原地。
我们可以将整个问题抽象成下面的图进行解答:
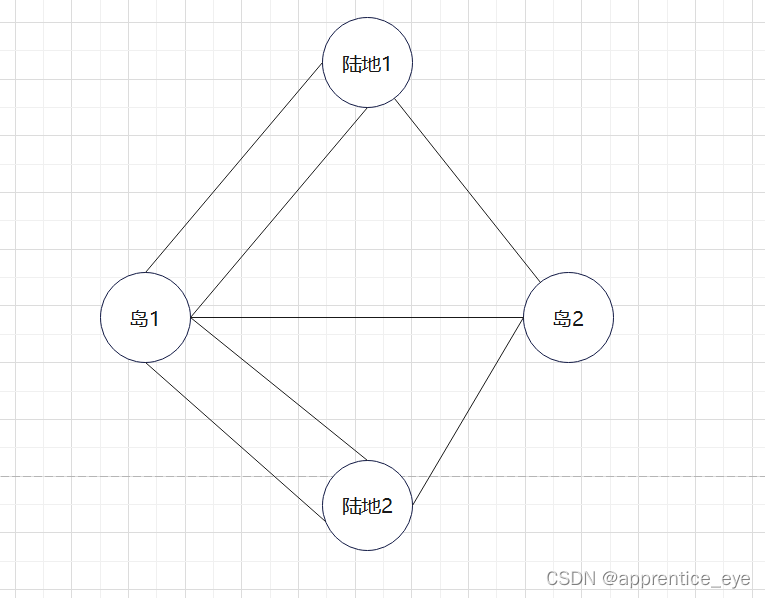
如果我们将每个节点与其他边数查出来(即数出每个节点的度数)这样就有下面的列表:
| 名称 | 度数 |
|---|---|
| 陆地1 | 3 |
| 陆地2 | 3 |
| 岛1 | 4 |
| 岛2 | 3 |
对于一个结点来说,每出一次节点,代表与结点相连的某一条边已经走过了即结点度数减1,与其相连的结点的度数也减1,如果上述哥尼斯堡有解的话,就应该存在这样一条回路从某个地点出发最后回到某个地点。
每走过一条边会导致这条边的两个端点的度数减1,如下图所示:

| 名称 | 度数 |
|---|---|
| 陆地1 | 3-1=2 |
| 陆地2 | 3 |
| 岛1 | 4-1=3 |
| 岛2 | 3 |
也就是说如果能够不重复的走过所有的桥,最后各个结点的度数一定为0.即
| 名称 | 最终不断计算度数变化 |
|---|---|
| 陆地1 | 0 |
| 陆地2 | 0 |
| 岛1 | 0 |
| 岛2 | 0 |
如果七桥问题有解,由于最终是回到起点,所以走的路径一定是回路

假设在七桥问题中存在这样一条回路,先考虑回路除起点(终点)外的其他结点,那么进入某个结点之后应该能够出来,也就是每经过一个结点会造成结点的度数减2
也就是说非起点(终点)结点的度数一定得是偶数,才能经过不断的减2、减2最终变成0
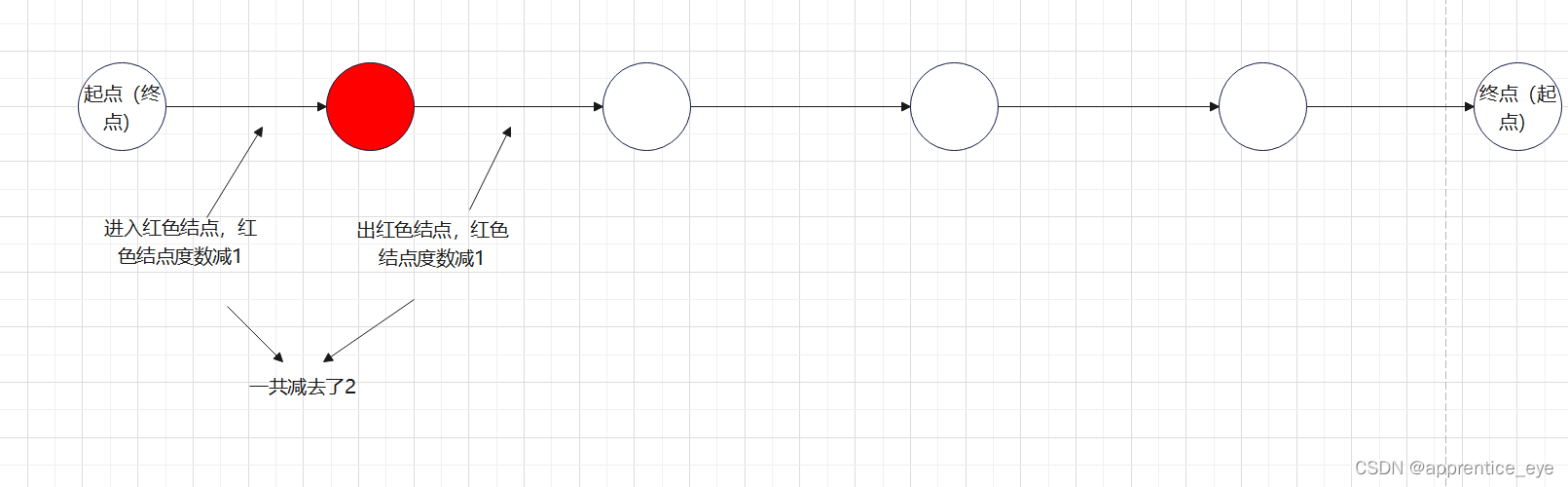
起点(终点)在最初的时候出了一次,度数减去1,在最终的时候回了一次,度数减去1,这样就减去了2,
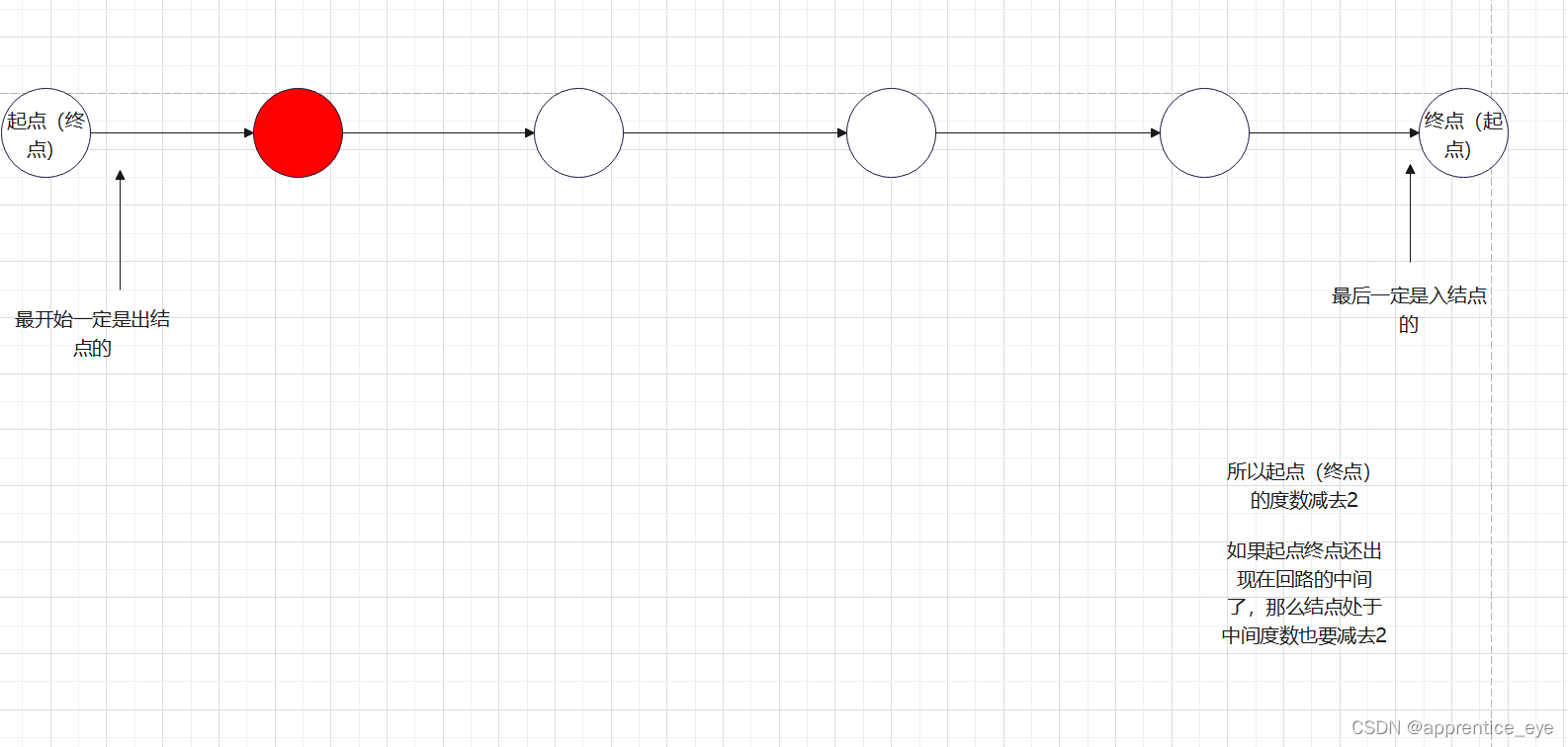
经过分析起点(终点)结点的度数一定得是偶数,才能经过不断的减2、减2最终变成0。
也就是说必须在所有结点的度数均为偶数的情况下,才能找到一条回路经过一次所有边且只经过一次。
欧拉在解决了哥尼斯堡七桥问题之后,提出并解决了一个更加一般性的问题:在什么样的图中能够找到通过图中每条边一次且仅一次的回路?
我们将能够在图中找到通过图中每条边一次且仅一次的通路(注意没有说回路)的图称为欧拉图。这样的通路叫做欧拉通路。具有欧拉通路的图叫欧拉图。
如何确定欧拉图
上边已经确定分析了具有欧拉回路的情况,因为是回路,所以其中所有的结点的度数都是偶数。
那么不是回路,但是通过所有的边一次且仅以此的通路,会让我们得出什么样的结论呢?
非起点或终点的结点,即路径中间的经过的结点,我们可以通过如下图的分析得到:

中间的结点仍然是减去2
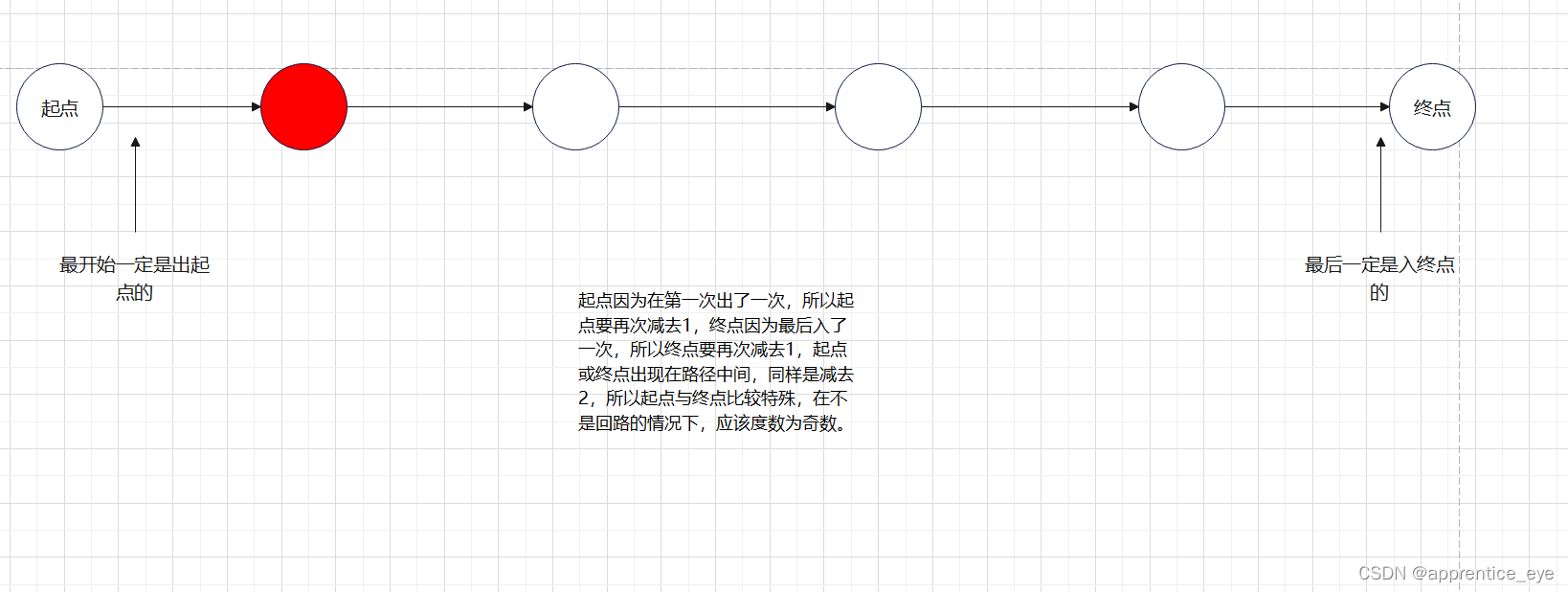
也就是说在欧拉通路不是回路的情况下,只有两个结点的度数为奇数,其余结点的度数均为偶数。
结合欧拉通路是回路的情况也就是说,一个图要是欧拉图,要么所有结点的度数均为偶数,要么其中两个结点的度数为奇数,其余结点的度数为偶数,即奇度数结点的个数为0或2.注:奇度数结点为2的是半欧拉图。图必须是连通的,不连通一定不是欧拉图。
欧拉图的应用
欧拉图可以用来解决一笔画问题、蚂蚁比赛问题、计算机鼓轮设计、中国邮路问题,这些问题在以后有时间了在进行讨论。
如果有什么地方讲的不好或者讲错的地方欢迎大家指出来,如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦! 我是你们的好伙伴apprentice_eye 一个致力于让知识变的易懂的博主。本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!