2024华数杯国际赛A题B题思路及代码！

大家好，这里是本次华数杯国际数学建模竞赛的AB题思路代码讲解贴。

关于思路，可以移步我的视频讲解：

2024华数杯国际赛数学建模选题建议及初步思路！_哔哩哔哩_bilibili

本篇主要讲解代码。

问题A：日本放射性废水

对于这次的华数杯A题，在我五月份完成的数维杯A题目中：

就已经完成过地下水污染物的公式推导：

因此，展示部分示例代码吧，我会在修改后，实际应用于我们这次的华数杯国际赛A题：

import numpy as np
import matplotlib.pyplot as plt

# 参数设定
L = 100.0  # 空间长度
T = 10.0   # 总模拟时间
Nx = 100   # 空间步数
Nt = 200   # 时间步数
D = 2.0    # 扩散系数
u = 1.0    # 对流速度

dx = L / Nx  # 空间步长
dt = T / Nt  # 时间步长

# 稳定性条件 (Courant-Friedrichs-Lewy 条件)
if u * dt / dx > 1:
    raise ValueError("稳定性条件未满足，请调整步长")

# 初始条件（在中心放置污染源）
C = np.zeros(Nx)
C[int(Nx / 2)] = 1.0

# 对流-扩散方程的数值解
for n in range(1, Nt):
    C[1:-1] = C[1:-1] - u * dt / (2 * dx) * (C[2:] - C[:-2]) + D * dt / dx**2 * (C[2:] - 2 * C[1:-1] + C[:-2])

# 绘制结果
plt.plot(np.linspace(0, L, Nx), C, label=f"t = {T}")
plt.title("对流-扩散方程的数值解")
plt.xlabel("位置")
plt.ylabel("浓度")
plt.legend()
plt.show()

问题B：光伏发电

对于这道题目而言，思路我也已经在上一个文章中讲解，所以我先分享一下数据吧：

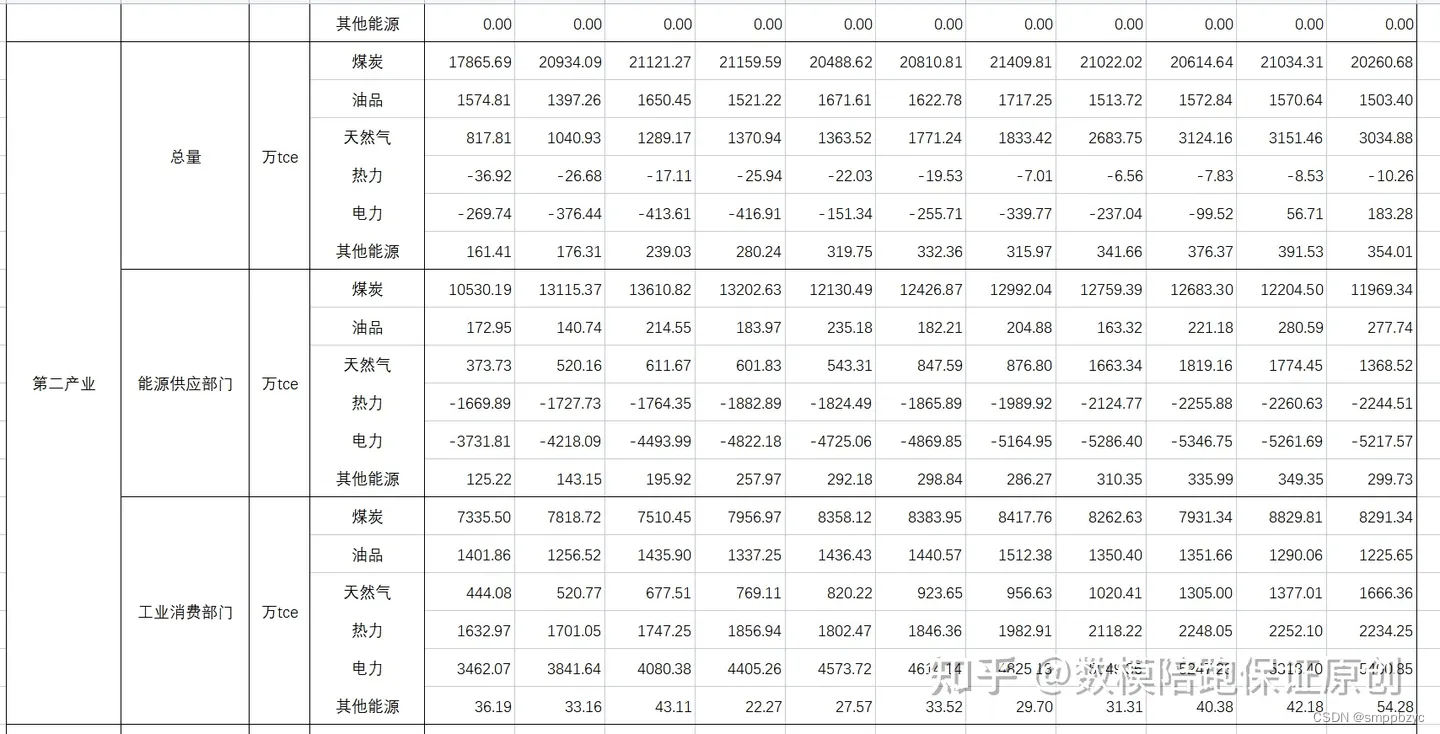
示例代码：

import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt

# 示例数据加载（您需要替换为实际的电力供应数据）
# 假设数据格式为两列：'Date' 和 'Electricity_Supply'
data = pd.read_csv('your_data.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

# 数据可视化（初步了解数据走势）
data.plot()

# ARIMA模型建立
# 参数(p,d,q)需要根据您的数据调整
model = ARIMA(data, order=(5,1,0))
model_fit = model.fit()

# 预测
# 这里预测从2024年到2060年的数据
forecast = model_fit.forecast(steps=36)
forecast.plot()

# 显示图表
plt.show()

以上免费数据表格，以及我之前的数维杯A题完整讲解视频都可以免费观看获取哈，此外，本次华数杯国际赛我会优先更新A题完整论文，预计在1.18号中午前更新，请点击我的下方个人卡片查看↓：