复杂网络基础

原文链接：02［复杂网络建模］第一讲：复杂网络的由来_哔哩哔哩_bilibili

目录

1.1复杂网络背景简介

1.2常用的复杂网络建模工具

1.3Python编程基础

创建一个简单的图

获取图的邻接矩阵

已知图的邻接矩阵，创建图

加权图

度、平均度以及度分布

路径和距离

连通性

集聚系数

---

1.1复杂网络背景简介

将人物抽象成节点，人物之间的关系抽象成连边

网络在自然和人类社会中无处不在，在每个系统的背后都有一个网络，他定义了组件之间的交互。

从社交网络到万维网，网络以一种无处不在的方式来组织各种现实世界的信息。

路径：是由网络的链接运行的路由；路径的长度表示路径包含的链接数。

在网络科学中，更多的是关注两个节点i和j之间的最短路径长度。

最短路径长度通常被称为它们之间的距离；

?

备注：平均距离---网络有多小

注意：为无向网络，以及任意一对节点

备注：Li表示邻居节点存在连边的数量

1.2常用的复杂网络建模工具

NetworkX — NetworkX documentation

igraph – Network analysis software(大规模的复杂网络)

备注：提供给图的算法并不是很丰富

Gephi - The Open Graph Viz Platform(针对可视化)

Snap.py Reference Manual — Snap.py 6.0 documentation (stanford.edu)

备注：用C++编写，具有很高的计算性能

graph-tool：使用 python 进行有效的网络分析 (skewed.de)

NetworKit

1.3Python编程基础

创建一个简单的图

import networkx as nx
import matplotlib.pyplot as plt  # 引入matplotlib.pyplot

# 创建一个空图
G = nx.Graph()
G.add_nodes_from([1, 2, 3, 4])
G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4)])

# 可视化
nx.draw(G, node_size=500, with_labels=True)

plt.show()  # 显示图形

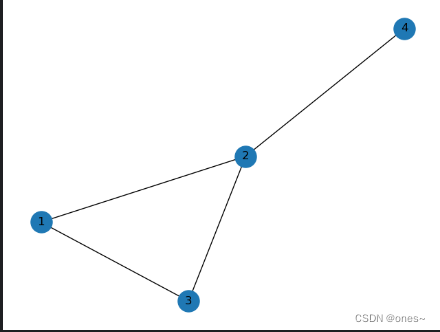
获取图的邻接矩阵

As=nx.adjacency_matrix(G)
A=As.todense()
print(A)

已知图的邻接矩阵，创建图

加权图

import networkx as nx

G=nx.Graph()
G.add_weighted_edges_from([(0,1,3.1),(1,2,7.5),(0,2,1.5)])
As=nx.adjacency_matrix(G)
print(As.todense())

度、平均度以及度分布

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G=nx.Graph()
#添加节点
G.add_nodes_from([1,2,3,4])
#添加边
G.add_edges_from([(1,2),(2,3),(2,4),(3,4)])
#获取网络G的度
d=nx.degree(G)
d=dict(nx.degree(G))
print(d)
print("平均度为：",sum(d.values())/len(G.nodes))

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G=nx.Graph()
#添加节点
G.add_nodes_from([1,2,3,4])
#添加边
G.add_edges_from([(1,2),(2,3),(2,4),(3,4)])
#获取网络G的度d
d=nx.degree(G)
d=dict(nx.degree(G))
print(d)
print("平均度为：",sum(d.values())/len(G.nodes))
#获取度分布
nx.degree_histogram(G)
x=list(range(max(d.values())+1))
y=[i/len(G.nodes) for i in nx.degree_histogram(G)]
print(x)
print(y)
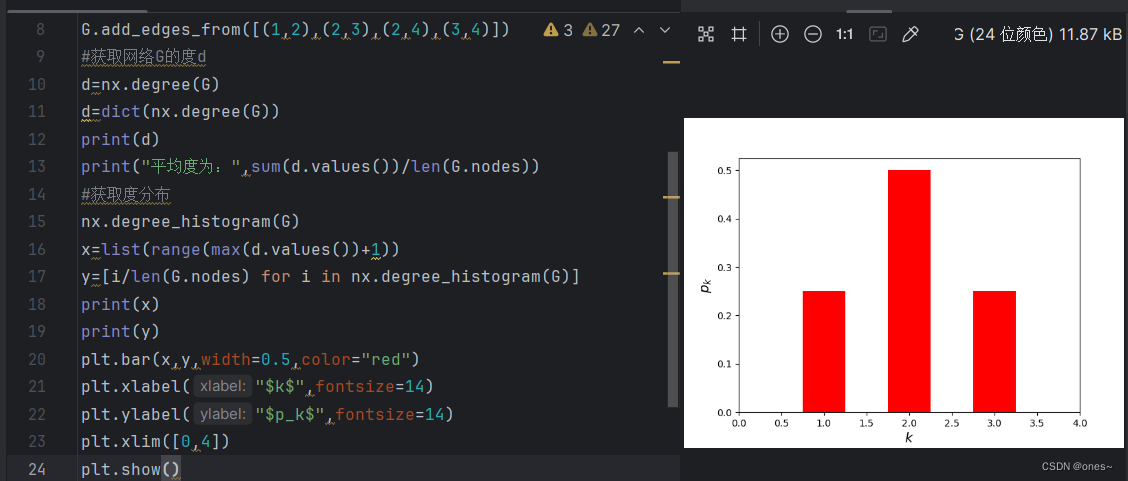
plt.bar(x,y,width=0.5,color="red")
plt.xlabel("$k$",fontsize=14)
plt.ylabel("$p_k$",fontsize=14)
plt.xlim([0,4])
plt.show()

路径和距离

连通性

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G=nx.Graph()
#添加节点
G.add_nodes_from([1,2,3,4,5,6,7])
#添加边
G.add_edges_from([(1,2),(1,3),(2,3),(4,7),(5,6),(5,7),(6,7)])
nx.draw(G,node_size=500,with_labels=True)

Gb=nx.Graph()
#添加节点
Gb.add_nodes_from([1,2,3,4,5,6,7])
#添加边
Gb.add_edges_from([(1,2),(1,3),(2,3),(2,4),(4,7),(5,6),(5,7),(6,7)])
nx.draw(Gb,node_size=500,with_labels=True)
print(nx.is_connected(G))
print(nx.is_connected(Gb))

集聚系数

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G=nx.Graph()
#添加节点
G.add_nodes_from([1,2,3,4,5,6,7])
#添加边
G.add_edges_from([(1,2),(2,3),(2,4),(2,5),(4,5),(4,6),(4,7),(5,7)])
nx.draw(G,node_size=500,with_labels=True)
print(nx.clustering(G,1))
#平均集聚系数
print(nx.average_clustering(G))
#全局集聚系数
print(nx.transitivity(G))
#plt.show()