数据结构第十章 排序

发布时间：2024年01月04日

排序的定义：计算机设计中的一种重要操作，它的功能是将一个数据元素的任意排序，重新排列成一个按关键字有序的序列

假设含n个记录(条件)的序列为

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?\left \{ {R_{1},R_{2},R_{3},R_{4}\cdot \cdot \cdot ,R_{n}}\right\}

其他相应关键字的序列为

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?K_{1},K_{2},K_{3}\cdot \cdot \cdot ,K_{n}

这里K1为1? Kn为n从小到大有记录顺序的排序,所以需要让他们满足下列关系排序：

? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ??R_{p1}<=R_{p2}<=R_{p3}\cdot \cdot \cdot <=R_{pn}

  • 排序稳定性：

    • 相同的关键字（52、52），通过排序算法排序后，顺序是否相同如果相同（52、52），算法是稳定算法
    • 如果不同（52、52），算法是不稳定算法。

  • 按照存储器不同分为：外部排序、内部排序

    • 内部排序：所有数据都在内存中进行的排序。适合数据量小的数据元素的排序。
    • 外部排序：排序过程中，需要访问外部存储器的排序。待排序的数据元素非常多必须存储在外部存储器上。

  • 按照相同关键字排序前后的位置分为：稳定排序、不稳定排序。例如：{3,4,2,3,1}

    • 稳定排序：相同关键字间的前后位置关系在排序前和排序后保持一致。例如：{1,2,3,3,4}
    • 不稳定排序：保持不一致。例如：{1,2,3,3,4}

简单的排序方法，时间复杂度：O(n^{2})

先进的排序方法，时间复杂度：O(n\log n)

基数排序，时间复杂度：O(d\cdot n)

1.直接插入排序

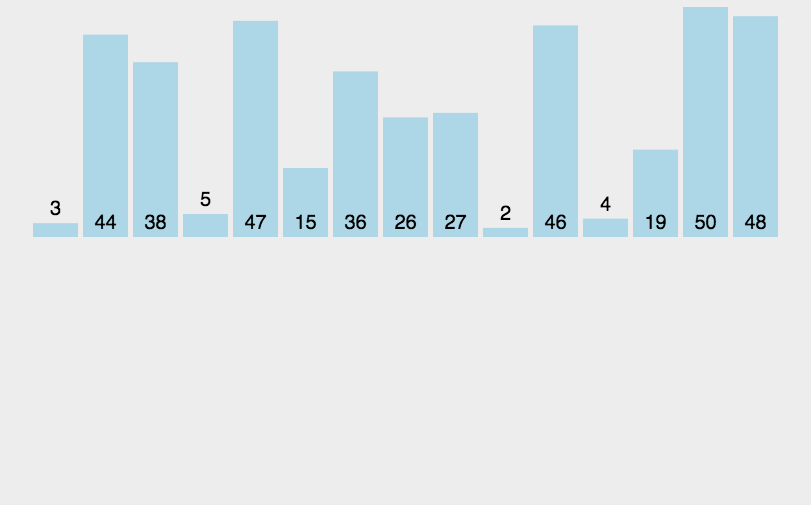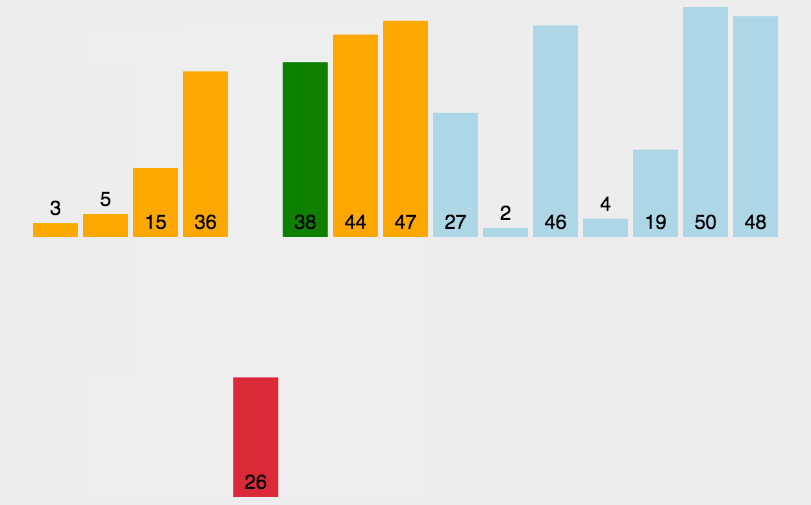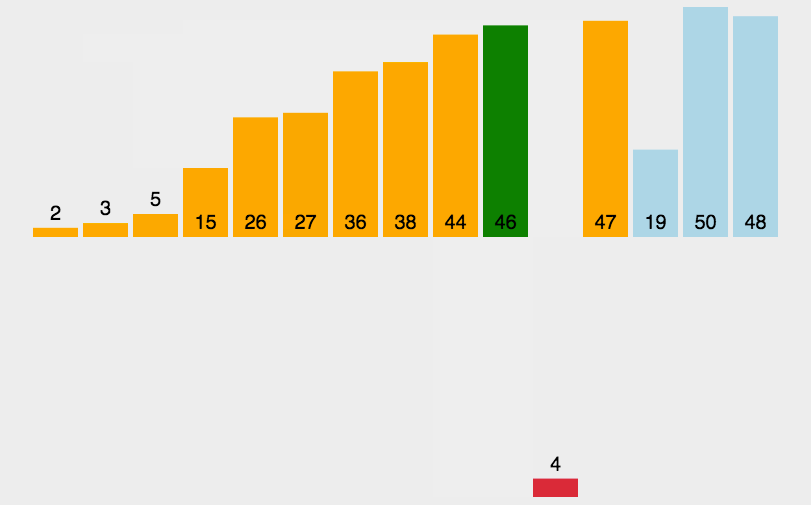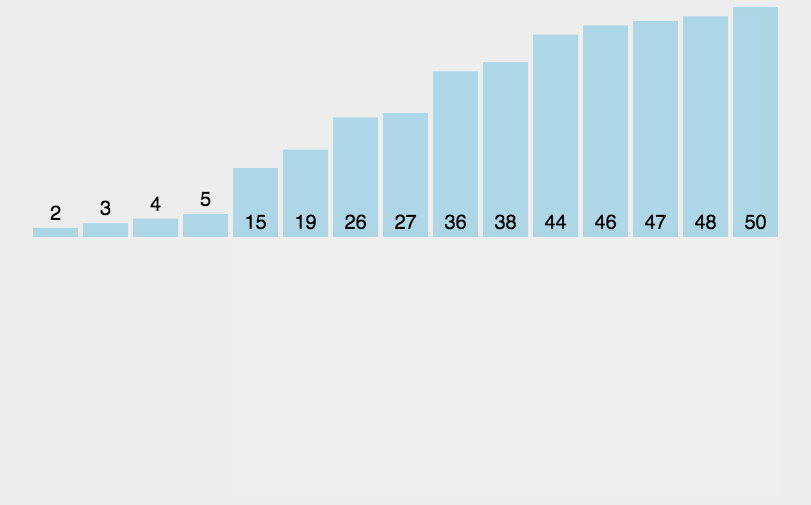
将整个插入的数分成两个部分，前面已经排好的是有序的，后面是无序的，整个过程就是将无须的变成有序的过程。

直接插入排序关键字为n，最多或者最少为n-1，时间复杂度为O(n^{2}),空间复杂度为O_{1}

算法为：

void InsertSort(SqList &L)
{

? ? int i,j;
? ? for(i=2;i<=L.length;i++){
? ? ? ? if(L.r[i].key < L.r[i-1].key)
? ? ? ? {

? ? ? ? ? ? L.r [0] = L.r[i];
? ? ? ? ? ? L.r [i] = L.r[i-1];//哨兵
? ? ? ? ? ? for(j=i-2;L.r[0].key < L.r[j].key ; j--)
? ? ? ? ? ? ? ? L.r [j+1]=L.r[j];
? ? ? ? ? ? L.r [j+1]=L.r[0];
? ? ? ? }
? ? }
}
2.折半插入

low mid high ,方式和折半查找类似

3.快速排序

起泡排序：使关键字最大的记录被安置到最后一个记录的位置上，然后进行第二趟起泡排序，对前n-1个记录进行同样操作

总时间复杂度：O(n_{2})

可选第一个记录作为枢纽

4.选择排序

在每一趟记录中选取最小的记录作为有序序列中的第i个记录

文章来源:https://blog.csdn.net/yst12138/article/details/135380750
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章