力扣精选算法100题——四数之和(双指针专题）

上一篇讲到（俩数之和and三数之和）这一篇我要来解析四数之和，四数之和建立在三数之和的基础上，我们需要熟练掌握三数之和的算法原理，如果大家三数之和还没弄清楚，请点击三数之和and二数之和链接即可看到。

?三数之和和四数之和的题意其实都一样。

第一步：了解题意

找到出四个数之和等于target即可，但是下标不能相同，且是不重复的四元组，比如[-2,0,0,2]和[-2,2,0,0]是一样的，所以也告诉我们需要去掉重复值的。

第二步：算法原理

首先先排序 sort函数进行排成降序

还是和三数之和的算法原理相似

👉1.先固定一个a值

👉2.在a后面的区间内，利用"三数之和“算法思路找到三个数，使这三个数的和等于target-a;

? ? ???这里的"三数之和"指的是什么呢？——就是利用三数之和的算法原理。

? ? ? ??🎈1.固定一个b值

? ? ? ??🎈2.在b后面的区间内，利用”双指针“算法，快速找到2个数和为target-a-b;

所以我们可以根据算法原理知道和三数之和的代码雷同，但是不一样的地方是这里需要固定2个值。所以就对一些地方进行改进即可。

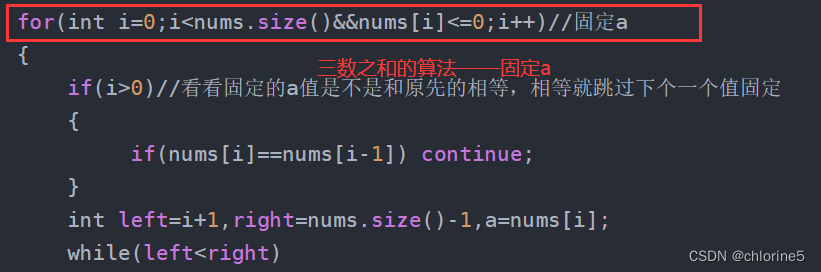
根据”三数之和“的算法分析，这里也是需要去重和防止漏值的。

?去重

🚩left和right去重

首先[left,right]区间内，我们看到如果left到达-2，right到达2的位置。

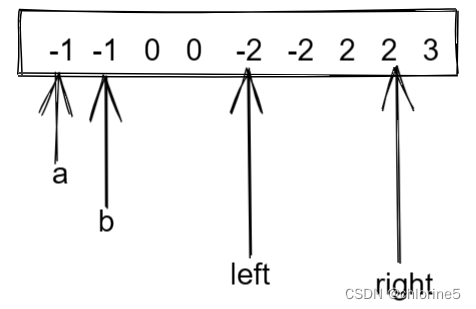我们可以在这里对Left和right的值进行判断去重，如果相等就Left++，right--，直到遇到与上一个值不相等的就继续进行。

?🚩固定a和b值

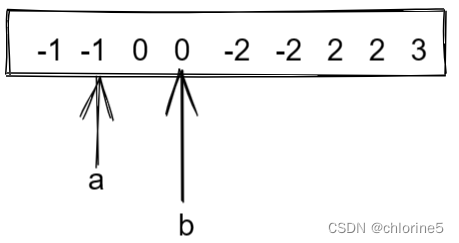
我们看到a的值前面一个值1和现在的值是一样的，b的值前面一个值0和现在的值是一样的，所以我们这里也是需要去重的。

所以[left,right]和固定a，固定三者的去重是缺一不可的，因为题意说明不能取重复的值。

---

?防漏

防漏其实就是left+right对应的值等于target-a-b的值，但是这时候我们不能就停止了。因为在[left,right]区间内还有更小的区间存在left+right对应的值等于target-a-b,比如下面的情况：

left和right对应的值相加等于-1，等于target-a-b=-1,但是我们还可以看到left++和right--更小的区间内也有符合条件的值。

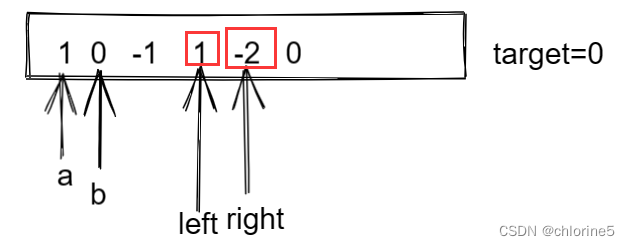
所以和三数之和的算法原理分析一样的，遇到符合条件的值存入之后我们需要缩小区间。

---

第三步：实现代码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target)
    {
        vector<vector<int>> ret;
        //排序
        sort(nums.begin(),nums.end());
        if(nums.size()<=2)
        {
            return ret;
        }
        //利用双指针解决问题
        for(int i=0;i<nums.size()-3;i++)//固定a
        {
            if(i>=1)//去重a
            {
                if(nums[i]==nums[i-1])continue;
            }
            for(int j=i+1;j<nums.size()-2;j++)//固定b
            {
                if(j>=i+2)//去重b
                {
                    if(nums[j]==nums[j-1])continue;
                }
                long long a=nums[i],b=nums[j],left=j+1,right=nums.size()-1;
                while(left<right)
                {
                    if(nums[left]+nums[right]<target-a-b)
                    {
                        left++;
                        while(left<right&&nums[left]==nums[left-1])
                        {
                        left++;
                        }
                    }
                    else if(nums[left]+nums[right]>target-a-b)
                    {
                        right--;
                        while(left<right&&nums[right]==nums[right+1])
                        {
                            right--;
                        }
                    }
                    else
                    {
                        ret.push_back({nums[i],nums[j],nums[left],nums[right]});
                        left++;//防漏
                        while(left<right&&nums[left]==nums[left-1])去重
                        {
                            left++;
                        }
                        right--;防漏
                        while(left<right&&nums[right]==nums[right+1])去重
                        {
                            right--;
                        }
                    }
                }
            }
        }
        return ret;
    }
};

我是我自己码头