MATLAB学习笔记（一）求解三阶微分方程

发布时间：2023年12月24日

一、求解三阶微分方程

? ? ? ? 对于多变量三阶微分方程求解问题，这里介绍一种求解方法。

例题如下：

? ? ? ? \ddot{x}_{1}+\dot{x}_{1}+x_{1}-\dot{x}_{2}-x_{2}=0

\dddot{x}_{2}+\ddot{x}_{2}+\dot{x}_{2}+x_{2}-\ddot{x_{1}}-\dot{x_{1}}-x_{1}=0

? ? ? ? 对于以上方程，给定边界条件，x_{2}\mid _{t=0}=0，\dot{x}_{2}\mid _{t=0}=0，\ddot{x}_{2}\mid _{t=0}=0，{x}_{1}\mid _{t=0}=0，\dot{x}_{1}\mid _{t=0}=0。求解x_{1}和x_{2}的表达式。

二、解题步骤

（1）建立辅助变量h（t表示自变量），令h\left ( 1 \right )=x_{1}，h\left ( 2 \right )=\dot{x}_{1}，h\left ( 3 \right )={x}_{2}，h\left ( 4 \right )=\dot{x}_{2}，h\left ( 5 \right )=\ddot{x}_{2}；

（2）根据等式阶数确定向量个数，将每阶的求导依次写出来，由（1）可知，\frac{\mathrm{d} h(1)}{\mathrm{d} t}=h\left ( 2 \right )，\frac{\mathrm{d} h(3)}{\mathrm{d} t}=h\left ( 4 \right )，\frac{\mathrm{d} h(4)}{\mathrm{d} t}=h\left ( 5 \right )；

（3）在matlab中建立函数，fun=@(t,h)[h(2);h(4)+h(3)-h(2)-h(1);h(4);h(5);h(1)+h(2)-h(3)+h(4)+h(3)-h(2)-h(1)-h(3)-h(4)-h(5)];%%此时就是将每阶的求导表示出来

[t,h]=ode45(fun,[0,5],[0,0,0,0,0]);
%一阶导数
figure(1)
plot(t,h(:,2),t,h(:,4));
%二阶导数
figure(2)
plot(t,h(4)+h(3)-h(2)-h(1),t,h(:,5))；

（4）对x1和x2进行求解，画图如下，此方法可以有效得到解的图。

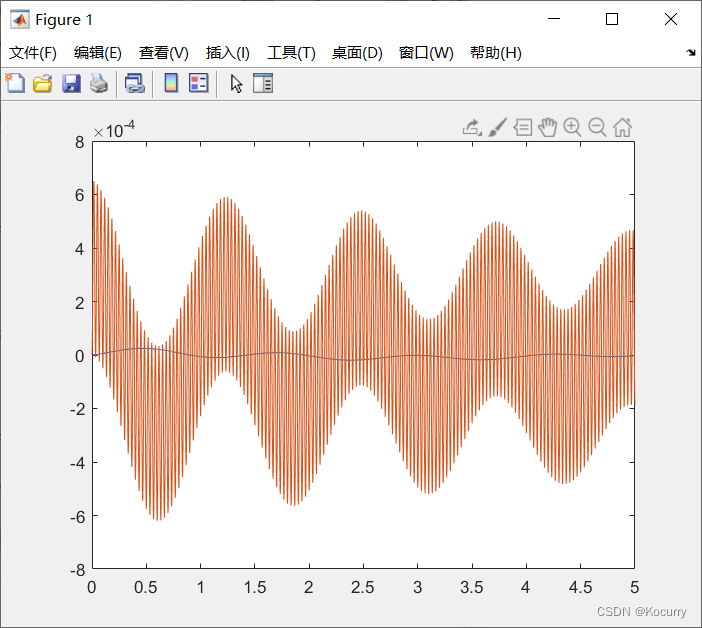
x1

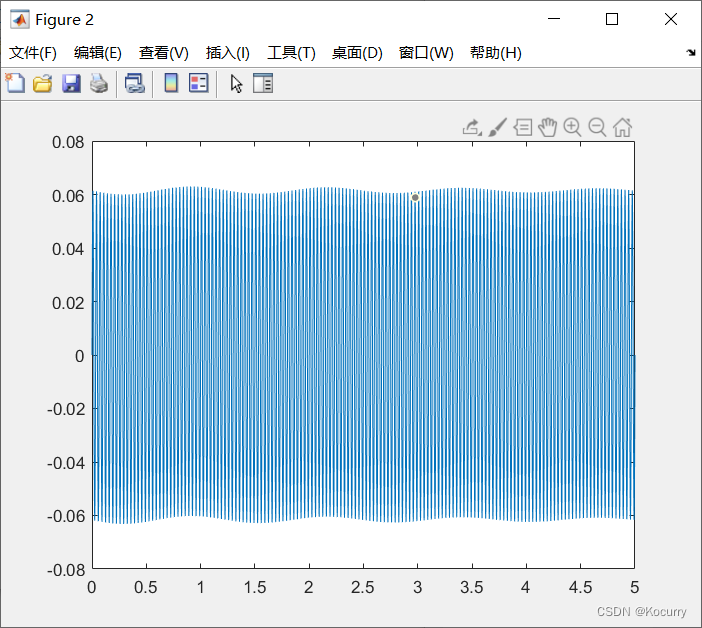
x2

文章来源:https://blog.csdn.net/weixin_38452841/article/details/135183547
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章