面试算法118：多余的边

题目

树可以看成无环的无向图。在一个包含n个节点（节点标号为从1到n）的树中添加一条边连接任意两个节点，这棵树就会变成一个有环的图。给定一个在树中添加了一条边的图，请找出这条多余的边（用这条边连接的两个节点表示）。输入的图用一个二维数组edges表示，数组中的每个元素是一条边的两个节点[u，v]（u＜v）。如果有多个答案，请输出在数组edges中最后出现的边。
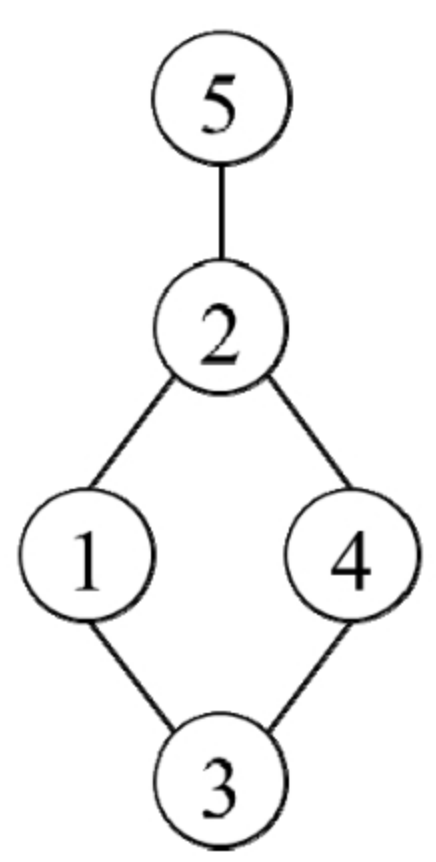
例如，如果输入数组edges为[[1，2]，[1，3]，[2，4]，[3，4]，[2，5]]，则它对应的无向图如图15.25所示。输出为边[3，4]。

分析

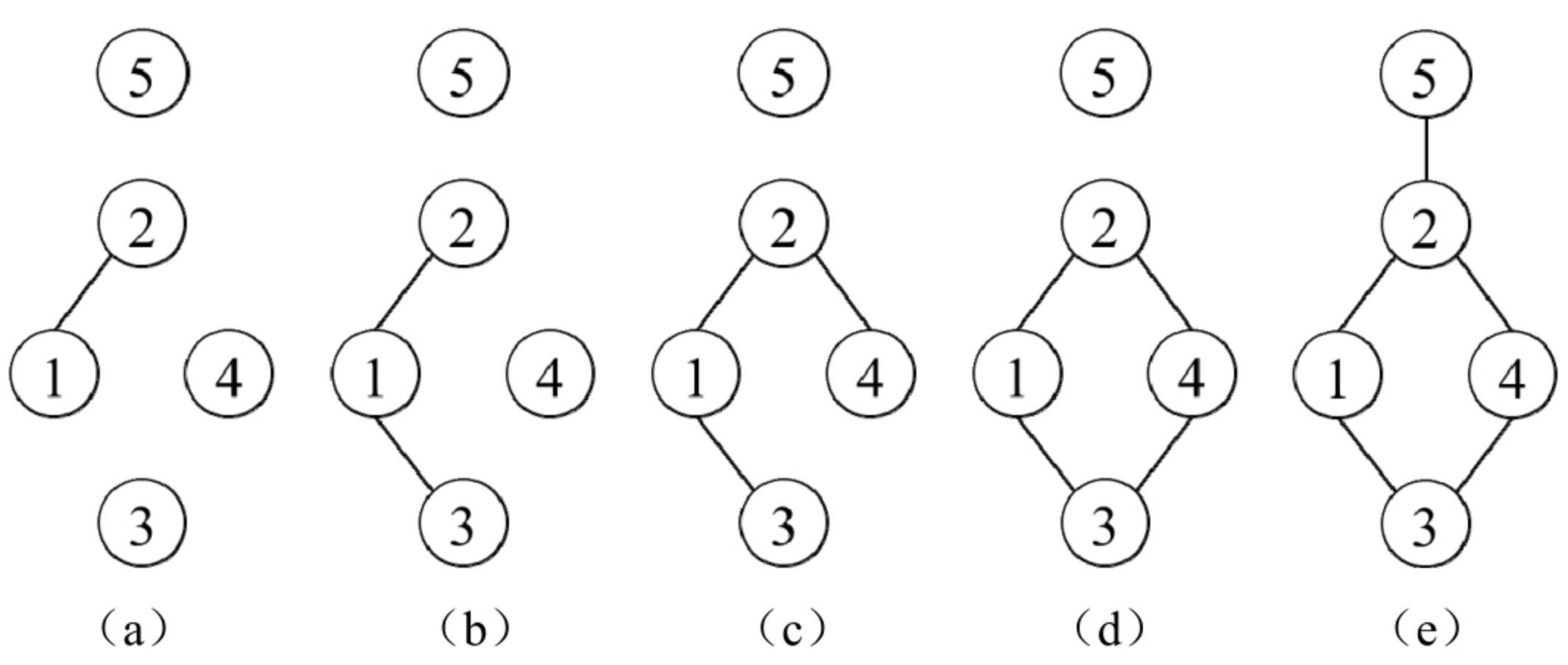
先在图中添加一条边[1，2]，于是将节点1和节点2所在的子图连在一起，形成一个有两个节点的子图，如图（a）所示。接下来添加一条边[1，3]。由于节点1和节点3分别属于两个不同的子图，添加这条边就将两个子图连成一个包含3个节点的子图，如图（b）所示。再在图中添加一条边[2，4]。由于节点2和节点4分别属于两个不同的子图，添加这条边就将两个子图连成一个包含4个节点子图，如图（c）所示。然后在图中添加一条边[3，4]。此时节点3和节点4属于同一个子图，添加边[3，4]导致图中出现了一个环，如图（d）所示。最后添加边[2，5]。节点2和节点5属于不同的子图，这条边将两个子图连在一起形成一个包含5个节点的子图。

解

public class Test {
    public static void main(String[] args) {
        int[][] edges = {{1, 2}, {1, 3}, {2, 4}, {3, 4}, {2, 5}};
        int[] result = findRedundantConnection(edges);
        System.out.println(result[0] + " " + result[1]);
    }

    public static int[] findRedundantConnection(int[][] edges) {
        int maxVertex = 0;
        for (int[] edge : edges) {
            maxVertex = Math.max(maxVertex, edge[0]);
            maxVertex = Math.max(maxVertex, edge[1]);
        }

        int[] fathers = new int[maxVertex + 1];
        for (int i = 1; i <= maxVertex; i++) {
            fathers[i] = i;
        }

        for (int[] edge : edges) {
            if (!union(fathers, edge[0], edge[1])) {
                return edge;
            }
        }

        return new int[2];
    }

    private static boolean union(int[] fathers, int i, int j) {
        int fatherOfI = findFather(fathers, i);
        int fatherOfJ = findFather(fathers, j);
        if (fatherOfI != fatherOfJ) {
            fathers[fatherOfI] = fatherOfJ;
            return true;
        }

        return false;
    }

    private static int findFather(int[] fathers, int i) {
        if (fathers[i] != i) {
            fathers[i] = findFather(fathers, fathers[i]);
        }

        return fathers[i];
    }

}