【研究】聚焦型光场相机等效多相机模型及其运动恢复结构应用

摘要:聚焦型光场相机在运动恢复结构(SFM)和场景重建等领域中的作用日益显现。但是传统SFM算法因聚焦型光场相机具有特殊的结构而难以直接应用。针对这一问题提出一种完整的聚焦型光场相机等效多目相机模型。在此基础上，利用传统多目相机的SFM算法，给出了适用于聚焦型光场相机的位姿估计算法示例和点云三角化算法示例。最后，通过仿真实验和真实场景重建实验验证了本文等效多目相机模型和SFM算法的正确性，进而表明聚焦型光场相机的SFM问题可以等价为多目相机的SFM问题。

关键词:机器视觉；聚焦型光场相机；多目相机模型；运动恢复结构；场景重建；位姿估计；三角化

1引言

光场相机能够同时捕捉光线的空间分布和角度分布信息，进而可以记录场景的深度信息，这使得光场相机能够应用于三维重建[1]、速度距离测量[2-3]以及运动恢复结构(SFM)等诸多领域。相比于非聚焦型光场相机[4]，聚焦型光场相机[5]可以在相似的相机配置条件下实现更高的深度计算精度，因此更适用于运动恢复结构(SFM)等领域。

运动恢复结构(SFM)的主要研究内容是从一个移动相机拍摄得到的一系列二维图像中恢复相机姿态和场景结构。很多学者[6-8]在SFM领域做了大量研究。目前较为流行的是Schonberger等[9]提出的COLMAP方法。但是这些方法仅适用于针孔相机，难于直接应用于聚焦型光场相机。

近几年，很多学者提出了适用于非聚焦型光场相机的SFM方法。Johannsen等[10]首次提出了适用于光场相机的SFM算法—LF-SFM。Zhang等[11]提出了基于直线和平面特征的SFM流程。Nousias等[12]提出了基于大规模无序排列的非聚焦型光场图像集合的场景重建算法。但是由于聚焦型光场相机和非聚焦型光场相机的结构和参数不同，聚焦型光场相机无法像非聚焦型光场相机那样便捷地提取子孔径图像，因此非聚焦型光场相机的SFM方法并不能直接应用于聚焦型光场相机。

为此，Zeller等[13]提出了适用于聚焦型光场相机的场景重建算法，分析了聚焦型光场相机等效多目相机模型中相机的空间位置。但是该方法在计算相机位姿过程中，将光场相机退化为针孔相机模型，且利用全聚焦图像对准来进行光场相机的位姿估计，故没有充分利用多目相机模型相比于针孔模型的优势，并且Zeller等[13]并没有给出完整的聚焦型光场相机等效多目相机模型，尤其是没有给出每个子相机的内参矩阵。

本文针对聚焦型光场的SFM问题，提出了完整准确的聚焦型光场相机的等效多目相机模型。并基于等效多目相机模型，利用多目相机的SFM方法，给出了适用于聚焦型光场相机的位姿估计方法和点云三角化方法。最后，通过仿真实验和真实场景重建实验验证了本文等效模型的正确性，证实了位姿估计方法和点云三角化方法的有效性，进而表明聚焦型光场相机SFM问题可以等效为多目相机SFM问题。

2 聚焦型光场相机基本概念

2.1相机结构

聚焦型光场相机可以划分为均一焦距的聚焦型光场相机[14]和多焦距聚焦型光场相机[15]。本研究以多焦距聚焦型光场相机为例进行说明，因为均一焦距可以视为多焦距的特例。聚焦型光场相机的成像平面可以位于微透镜阵列(MLA)的前侧或者后侧，前者对应开普勒结构，后者对应伽利略结构，如图1所示。目前的商用聚焦型光场相机(例如:Raytrix公司)多采用伽利略结构，其通过使用3类不同焦距的微透镜来增加景深范围

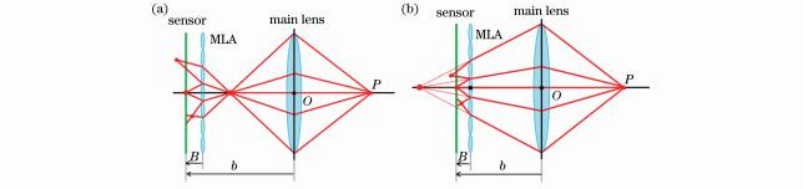
图1多焦距聚焦型光场相机结构示意。(a)开普勒结构;(b)伽利略结构

2.2坐标系建立

为了方便后续的描述，首先建立坐标系，并对相关符号进行说明。光场相机坐标系OXYZ的中心选在主透镜的中心位置O点，其Z轴方向与相机光轴重合，方向朝外。图像坐标系ouv的坐标原点选在传感器的左上角o点。具体的坐标系示意图如图2所示，图中fL为主透镜的焦距(mm)，b为传感器相对于主透镜的位移(mm)，B表示传感器相对于MLA的位移(mm)。值得注意的是，这里fL为正数，而b和B为负数。

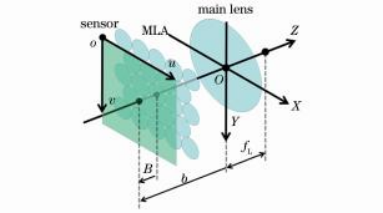
图2光场相机坐标系建立

2.3光场相机标定

在计算聚焦型光场相机等效多目相机模型的具体参数之前，需要得到聚焦型光场相机的具体相机标定参数。本研究采用Bok等[16]提出的光场相机内参{fx，fy，cu，cv，K1，K2}。这些内参和本文相机模型中参数的具体对应关系为

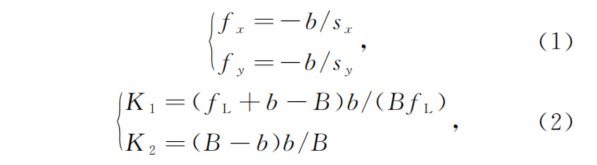
式中:fx和fy分别为x和y方向的像素焦距;(sx，sy)为传感器上像素的物理尺寸;(cu，cv)表示主镜头的中心O点在ouv中的像素坐标;K1，K2为光场相机区别于针孔相机的相机参数。

3 聚焦型光场相机等效多目相机模型

聚焦型光场相机本质上可以等价为多目相机阵列。假定在物空间存在物点P，其在相机坐标系OXYZ内的坐标为(Px，Py，Pz)，那么根据薄透镜成像公式，P点对应的像点Q的坐标满足

Qz=

，(3)

式中:Qz为Q点在相机坐标系OXYZ中的Z轴坐标值。进一步，将微透镜中心位置看作成像点，并根据薄透镜成像公式将微透镜中心坐标投影到真实空间中，进而得到

Lz=

，(4)

式中:Lz为微透镜中心投影后位置在OXYZ中的Z轴坐标值。将所有投影后的微透镜看作子相机的主镜头，就可以将聚焦型光场相机等效变换为虚拟的相机阵列。根据MLA平面距离主透镜的距离

b-B和主透镜焦距fL的关系，可得Lz的取值有正负之分。因此可以得到图3所示两种等效多相机模型，即fL>|b-B|和fL<|b-B|两种情况。

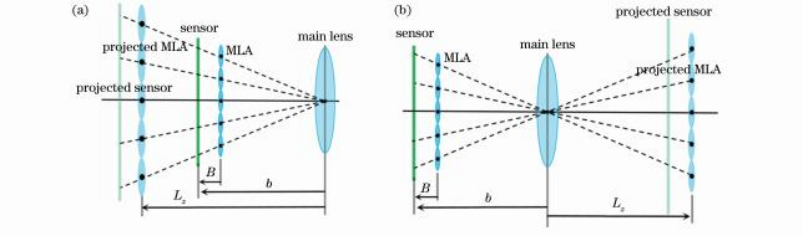
图3等效多目相机模型。(a)fL>|b-B|;(b)fL<|b-B|

3.1子相机位置姿态

在完成相机标定后，可以根据相机内参来确定等效多目相机模型中的子相机的物理空间位置和姿态。根据相似三角形关系，可以得到子相机中心坐标(Lx，Ly，Lz)和ouv下微透镜中心坐标(lu，lv)的关系为

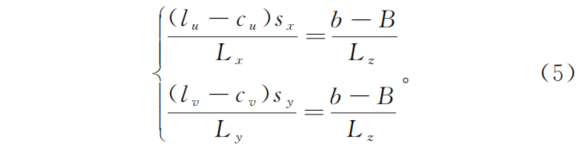
根据(2)式中K1和K2，结合(4)式，可以得到Lz=-K2/K1。进一步由(5)式可得

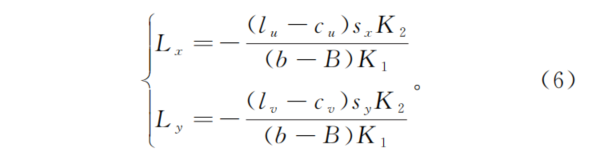
根据相似三角形关系，可以得到微透镜中心像素坐标(lu，lv)和微透镜图像中心像素坐标(iu，iv)的关系为

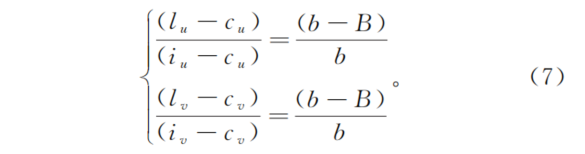
?根据(1)式、(6)式和(7)式可以得到虚拟相机阵列中每个子相机中心在OXYZ中的坐标为

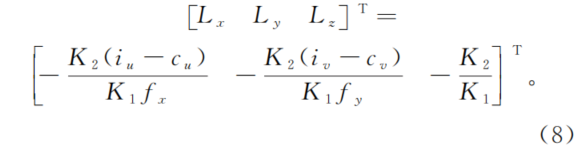
除了子相机中心位置，子相机的朝向也是需要确定的重要参数。由于MLA平面的所有微透镜共面且朝向统一，因此投影后得到的子相机中心位置也符合共面特性，且每个子相机的朝向相同。每个子相机的朝向与聚焦型光场相机的朝向保持一致。

在此基础上，建立子相机的相机坐标系O'JKL，如图4所示，其坐标系中心选在子相机的中心位置，坐标轴方向与相机坐标系OXYZ的坐标轴方向相同，与此同时，建立投影传感器的像素坐标系o'mn。对于空间内任意一个点P，令其在相机坐标系OXYZ内坐标为(Px，Py，Pz)，那么P在某一子相机坐标系O'JKL内的坐标(Pj，Pk，Pl)为

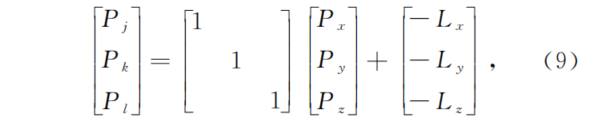
这样就得到了子相机坐标O'JKL相对于相机坐标系OXYZ的变换关系。

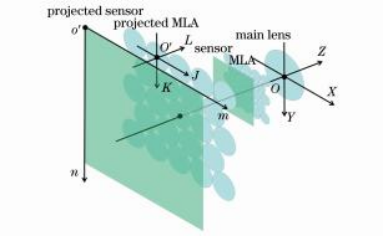
图4子相机坐标系建立示意图

3.2子相机内参矩阵

为了得到完整的多相机等效模型，需要推导出每个子相机的内参矩阵。根据Bok等[16]的工作，原始图上像素点p在标定后可以换算为相机外真实空间中的一根光线，该光线在OXYZ坐标系中的方向向量(rx，ry，1)和点p在ouv中的坐标(pu，pv)的关系为

假定点P是和像素点p相关的三维空间点，并用(Pj，Pk，Pl)表示P点在子相机坐标系O'JKL中的坐标，那么(Pj，Pk，Pl)和光线方向向量(rx，ry，1)的关系为

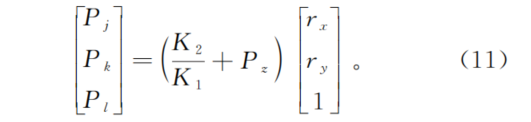
根据(10)式，(11)式变为

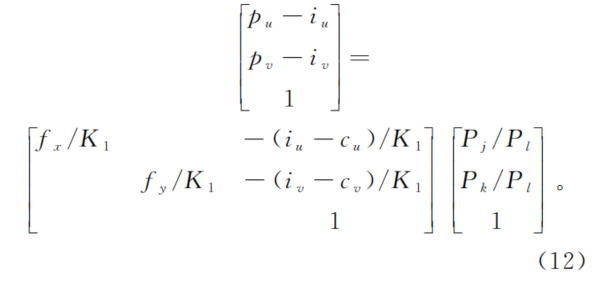
?(12)?式反映了(Pj，Pk，Pl)和原始图中特征坐标(pu，pv)的关系。为进一步得到(Pj，Pk，Pl)和子相机图像内特征坐标的关系，首先确定投影后传感器的位置，并建立子相机图像坐标系o″αβ。

??

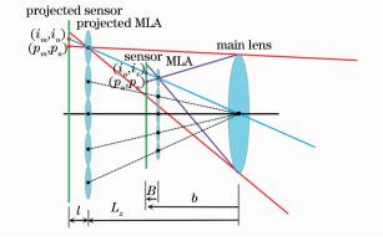
图5子相机图像和微透镜图像的对应关系

通过图5可以看出，投影后传感器上的图像形状和原始图上的微透镜图像形状是一致的。为了方便描述，本研究取投影后传感器和投影后MLA之间的间距为单位1，同时令投影后传感器的像素分辨率和原始图分辨率保持一致。假设微透镜图像中任意一点p在坐标系ouv下的坐标为(pu，pv)，并且p点对应的微透镜图像中心i点坐标为(iu，iv)。令(pm，pn)和(im，in)表示p点和i点在投影后传感器上对应位置在坐标系o'mn下的坐标，则三者满足

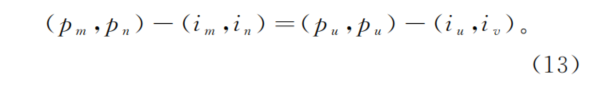
?为了更清晰地进行后续描述，建立子相机的图像坐标系o″αβ，如图6所示。对于o'mn中的特征坐标(pm，pn)，其在o″αβ中的坐标(pα，pβ)为

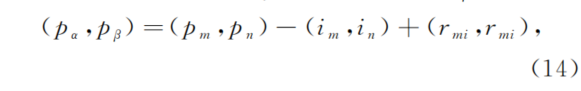
?式中:rmi为微透镜图像的像素半径，其在数值上等于投影后子相机圆形图像的像素半径。

根据(12)~(14)式，可以得到从(Pj，Pk，Pl)到(pα，pβ)的变换关系，即

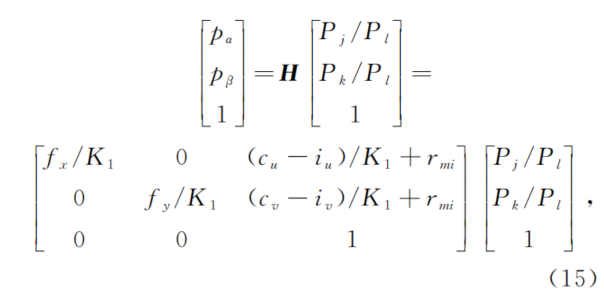
?式中:H为等效多目相机中子相机的内参矩阵。值得注意的是，不同位置的子相机的内参矩阵不是固定的，具体的变化体现在内参矩阵H需要根据微透镜图像中心坐标(iu，iv)的变化而变化。这是由于微透镜中心和微透镜图像中心并不总在一条水平直线上，故导致投影得到的子相机中心和子相机图像中心也并不总是在同一个水平直线上，如图6所示。

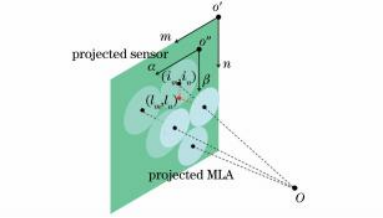
图6子相机图像坐标系建立示意图

3.3像素到光线的映射

在等效多相机模型的基础上，将不同子相机内的特征转换为光线坐标，便于使用基于光线的传统位姿估计算法和点云三角化算法。

具体来讲，本研究采用普吕克坐标[17]来进行光线的坐标表示。对于中心坐标为(Lx，Ly，Lz)的子相机，令其图像内的像素点p在坐标系o″αβ下的坐标为(pα，pβ)。根据(13)式和(14)式，可以得到p点在微透镜图像内对应的特征坐标(pu，pv)为

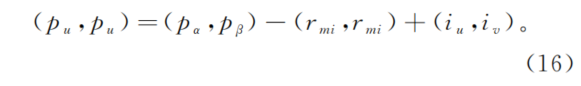
?根据(10)式，可以得到像素坐标为(pu，pv)的特征对应的光线(相机外)在聚焦型光场相机相机坐标系OXYZ下的方向向量为(rx，ry，1)。因为该光线必定通过子相机的中心(Lx，Ly，Lz)，所以光线弯矩(mr1，mr2，mr3)的计算公式为

?对于中心坐标为(Lx，Ly，Lz)的子相机，图像坐标为(pα，pβ)的特征点对应的特征光线在OXYZ下的普吕克坐标为

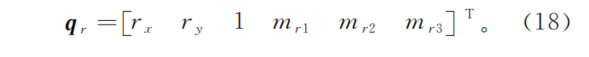
4?基于多目相机等效模型的SFM方法

本研究将聚焦型光场等效为多目相机阵列。对于多目相机，更一般的数学描述为非中心相机[18]。这里的非中心相机指的不是传统意义上的针孔相机，而是具有多个光线会聚中心的一般相机模型。非中心相机存在一个视点(viewpoint)，所有子相机相对于视点存在一定的旋转和位移，且每个子相机都有经过自己子相机中心的光线，具体的示意如图7所示。在实际应用过程中，非中心相机被当作一个整体看待。

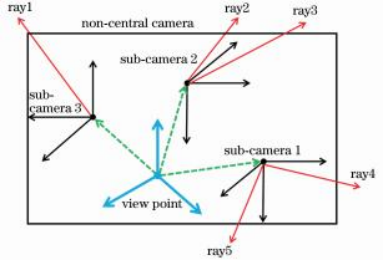
图7非中心相机示意图

对于聚焦型光场相机，其视点位于主镜头中心O点，相机坐标系OXYZ即为视点坐标系，故3.1节中的坐标系O'JKL即为子相机坐标系。(9)式描述了视角坐标系和子相机坐标的位置关系，(10)式、(17)式和(18)式是将像素特征转化为普吕克坐标表示的光线。

本节基于聚焦型光场相机的等效多目相机模型，利用非中心相机的SFM算法给出了适用于聚焦型光场相机的位姿估计算法和点云三角化算法示例，并以此证明聚焦型光场相机的SFM问题可以转化为多目相机的SFM问题。传统多目相机的SFM方法可以应用于聚焦型光场相机的SFM问题中。

4.1相对位姿估计

在SFM过程中，往往要利用两帧图像进行场景重建初始化，这其中涉及到两帧图像之间的相对位姿估计[9]。对于聚焦型光场相机，这一问题可以划归为非中心相机的相对位姿估计问题。本研究利用聚焦型光场相机的等效多相机模型，使用基于RANSAC方法[19]中的17点算法[20]进行两帧聚焦型光场相机图像之间的相对位姿估计。

具体来讲，假定两帧原始图具有Nm组匹配的特征点。对于第i组匹配特征点i=1，2，…，Nm，假定其在第1帧有mirrel个特征点，在第2帧有nirrel个特征点，利用3.3节的方法可以将所有特征点都换算成由普吕克坐标表示的光线，这样可以得到

个匹配的光线对。对于两帧之间的任意匹配光线，其普吕克坐标L1和L2满足

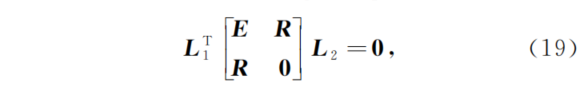
?式中:E为本质矩阵;R为两帧之间的旋转矩阵。假定向量t表示两帧之间的位移向量，那么本质矩阵E在数值上满足

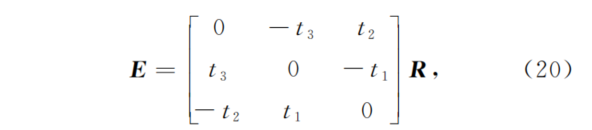
?式中:t1、t2和t3为向量t的元素分量。

将

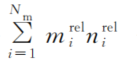
个匹配的光线对作为基于RANSAC方法中17点算法[20]的输入，可以计算得出从第2帧相机坐标系OXYZ到第1帧相机坐标系OXYZ的变换矩阵R和t。

4.2绝对位姿估计

在场景重建过程中，基于已有的重建点，对新图像帧进行注册的问题本质上就是绝对位姿估计的问题。根据聚焦型光场相机的等效多目模型，其绝对位姿估计问题可以划归为非中心相机的绝对位姿求解问题[18]，即利用nabs个二维点和三维点的对应关系来得到已标定非中心相机的位置和姿态。

在非中心相机的绝对位姿求解问题上，gP3P算法[21]具有较好的表现，故本研究采用基于RANSAC方法[19]的gP3P算法[21]进行绝对位姿估计。在实际计算过程中，一个空间三维点在原始图中对应多个二维特征点。设共计有Nabs个三维特征点可以在当前帧中找到匹配的二维特征，对于第j个三维特征点(j=1，2，…，Nabs)，在原始图中存在njabs个二维特征点与之对应，这样共计存在

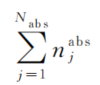
个二维点-三维点的对应关系。将所有二维点-三维点的对应关系作为基于RANSAC[19]的gP3P算法[21]的输入，就可以计算得到当前帧相对于三维点所在世界坐标系的绝对位置姿态。本研究在具体实现过程，利用文献[18]中公开的OpenGV代码库中的代码实现。

4.3点云三角化

在得到图像帧位置姿态后，需要根据两帧图像的匹配特征通过三角化算法计算出空间三维点在世界坐标系的坐标。具体来讲，对于一个任意的空间三维点，假设其在第1帧聚焦型光场相机原始图中具有mtri个匹配特征点，在第2帧中具有ntri个匹配特征点，那么根据聚焦型光场相机的多目等效模型，可知该问题可以等效为多视角(mtri+ntri视角)三角化问题，其中每个相机的内参矩阵可以通过(15)式得到，子相机的物理位置可以通过(8)式得到。本研究利用DLT算法[22]得到重建的三维点，并进一步利用Levenberg-Marquardt非线性优化算法[23]优化重投影误差，进而优化三维重建点的坐标。

5?实验与验证

为了验证本文等效多目相机模型和SFM算法的正确性，进行相应的仿真和真实实验。实验代码在win7操作系统上的MATLAB软件上运行。实验所用计算机的CPU为英特尔公司的i7-7700(3.6GHz)。本研究首先通过仿真实验验证本文等效模型的正确性。具体的聚焦型光场相机仿真参数如表1所示。传感器的分辨率为3000pixel×2000pixel。

根据表1仿真参数可以计算出相机内参{fx，fy，cu，cv，K1，K2}的具体取值，如表2所示。表2聚焦型光场相机标定内参取值

根据表2所示的仿真参数以及(8)式，可以得到等效相机阵列中子相机的最小物理间距为1.269mm，最远的子相机物理间距能够达到140.423mm。等效相机阵列呈六边形排布，共计有71×92个子相机。在仿真相机的基础上，测试了相对位姿估计、绝对位姿估计以及点云三角化算法的性能，进而验证了等效模型的正确性。

随后，使用Ratyrix公司的R29相机进行真实场景的拍摄，并基于拍摄的场景进行真实的场景重建实验。这一真实实验进一步验证了本文等效相机模型的正确性，并表明基于多目相机模型的SFM算法能够成功应用于聚焦型光场相机的场景重建中。

5.1相对位姿仿真测试

首先，基于仿真的聚焦型光场相机，测试4.1节中的相对位姿估计算法在不同噪声水平下的性能表现。对于两帧不同位置的聚焦型光场相机图像，令第1帧图像的相机坐标系OXYZ和世界坐标系OwXwYwZw重合，并随机产生第2帧图像的位置。具体来讲，从[-0.2m，0.2m]范围内随机产生第2帧图像相对于OwXwYwZw的位移，并在[-18°，18°]的范围内随机产生第2帧图像相对于OwXwYwZw中3个坐标轴的旋转角度。与此同时，在距离相机0.5~8.5m的范围内，随机产生200个空间三维点，并将三维点投影到光场原始图中。对于投影后的二维特征点位置，加入均值为0、均方差为σ的高斯噪声。实验中，改变噪声均方差σ的取值，观察位姿估计结果的精度。为了增加实验的一般性，对每个σ取值，共计进行100次独立实验。每次实验中，第2帧相机图像的姿态和三维点云都随机产生。实验中，衡量相对位姿估计准确度的评价指标为100次独立实验的相机位移误差和旋转角度误差的中值，具体计算结果如图8

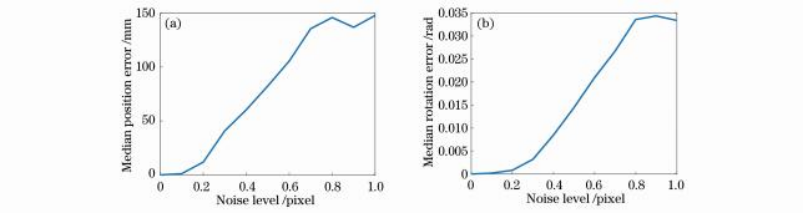
图8相对位姿估计结果。(a)位移误差中值;(b)旋转角度误差中值

从实验结果可以看出，基于等效多目相机模型的相对位姿估计算法具有较好的精度，并且估计精度和噪声水平大致呈线性关系，这验证了本文提出的等效多目相机模型的正确性，也说明该算法能够有效地解决聚焦型光场相机的相对位姿估计问题。

5.2绝对位姿估计仿真测试

在绝对位姿估计仿真实验中，本研究采用的相机参数和仿真参数与5.1节中的参数一致。具体的区别在于:在绝对位姿估计实验中，本研究根据三维空间点和第2帧图像的二维特征之间的对应关系，计算第2帧图像在世界坐标系中的位置和姿态，具体的计算结果如图9所示。

根据实验结果，基于等效多目相机模型的绝对位姿估计算法具有较好的位姿估计结果，这再次验证了本文提出的等效多目相机模型的正确性，也说明该算法能够有效地解决聚焦型光场相机的绝对位姿估计问题。

5.3点云三角化仿真测试

在点云三角化仿真实验中，本研究采用和5.1节中相同的仿真条件。具体的区别在于:点云三角化实验利用两帧光场图像之间的已知位姿和二维特征匹配关系，来计算对应的空间三维点，并通过三维点的空间误差来衡量点云三角化的精度。

实验中三角化精度的评价指标为100次独立实验中重建点云平均误差的中值，具体的计算结果如图10所示。该实验结果验证了本文提出的等效多目相机模型的正确性，也表明该三角化算法能够有效地解决聚焦型光场相机的点云三角化问题。

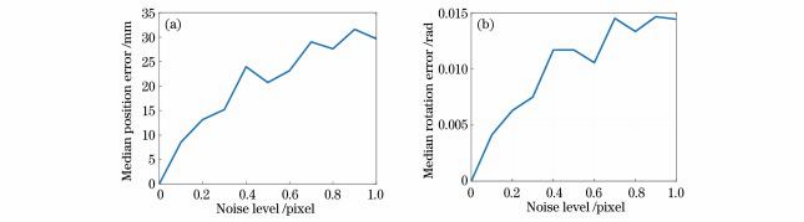
图9绝对位姿估计结果。(a)位移误差中值;(b)旋转角度误差中值

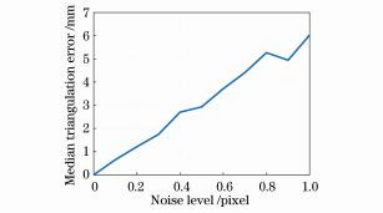
图10三角化结果

5.4真实场景重建实验

为了进一步验证本文等效多目相机模型的正确性，进行了真实场景重建实验。具体来讲，使用R29聚焦型光场相机搭配100mm焦距的主透镜，拍摄了15张真实场景的光场图像。实验中，被拍摄场景距离相机0.9m左右。具体的几幅原始图示例如图11所示。

图11R29拍摄的原始图

本文首先参照文献[24]中的实验，基于棋盘格标定板进行R29相机的标定，标定后的相机内参取值如表3所示。根据该参数，可以得到R29相机等效相机阵列的具体参数。相机阵列中最小子相机间距为6.46mm，最大子相机间距为1588.93mm，共计有158×206个子相机，且呈六边形排布。

在此基础上，利用R29相机配套软件RxLive得到15帧光场图像对应的深度图和全聚焦图。随后，在全聚焦图上提取SIFT特征，并结合SIFT特征在深度图中的虚深度[5]取值，将检测到的SIFT特征投影到原始图中，具体的SIFT特征在原始图的检测结果示例如图12所示。

图12SIFT特征检测结果示例

在得到原始图中的SIFT特征位置后，根据聚焦型光场相机的等效模型将二维特征投影为由普吕克坐标表示的光线，进而利用4.1、4.2和4.3节的方法进行位姿估计和点云三角化。

在具体的场景重建过程中，使用类似于COLMAP[9]的场景重建流程，结合4.1、4.2和4.3节的SFM算法，最终得到了真实物理尺度的场景重建结果和15帧相机的位置和姿态，如图13所示。

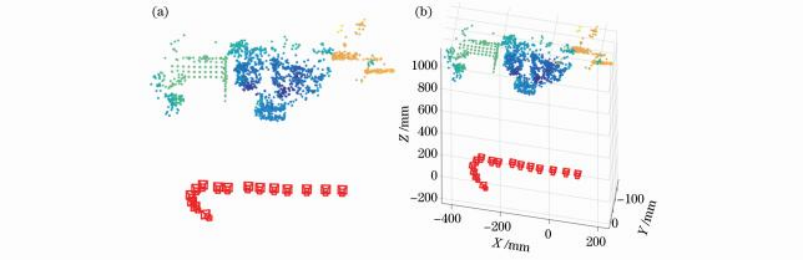
图13场景重建结果。(a)不带坐标轴;(b)带坐标轴

通过实验结果可以看出，本文场景重建实验能够正确恢复出场景的结构和物理尺度。这不仅可以验证本文提出的聚焦型光场相机等效模型的正确性，还说明了聚焦型光场相机的SFM问题可以等价为多目相机的SFM问题。

6?结论

针对聚焦型光场相机的运动恢复结构(SFM)问题，提出完整的聚焦型光场相机等效多目相机模型。基于该等效模型，给出适用于聚焦型光场相机的相机位姿估计算法和点云三角化算法示例。仿真实验和真实场景重建实验的结果验证了本文等效多目相机模型和SFM算法的正确性，并表明聚焦型光场相机的SFM问题可以转化为多目相机的SFM问题。

参考文献：

文章转自：光学学报，作者| 刘青松 ,谢晓方,张烜喆 ,田瑜 ,许晓军

声明：转载此文目的在于传递更多信息，仅供读者学习、交流之目的。文章版权归原作者所有，如有侵权，请联系删除。