第九章 排序
1.插入类排序:是在一个已排好序的记录子集的基础上,每一步将下一个待排序的记录有序插入已排好序的记录子集,直到将所有待排记录全部插入为止
a.直接插入排序(稳定)
b.折半插入排序(稳定)
c.希尔排序(不稳定)
2.交换类排序:通过一系列交换逆序元素进行排序
a.冒泡排序:通过对相邻的数据元素进行交换,一次交换只能消除一个逆序(稳定)
b.快速排序:一次交换可能消除多个逆序(不稳定)
3.选择类排序:每一趟在n-i+1(i=[1,n-1])个记录中选取关键字最小的记录作为有序序列中的第i个记录
a.简单选择排序(不稳定)
b.树形选择排序(稳定)
c.堆排序(弥补树形选择排序占用空间多的遗憾)(不稳定)
4.归并排序(分治思想):
a.分解。将一个长度为n的无序序列不断分解成两个规模大致相等的子序列,直到子序列大小为1.
b.合并。不断将两个有序子序列合并,得到一个新的有序序列。
分配类排序:利用分配和收集两种基本操作实现排序
a.多关键字排序
b.链式基数排序
c.基数排序(稳定)
1.下面四种排序算法中,稳定的算法是:(C)
A.堆排序
B.希尔排序
C.归并排序
D.快速排序
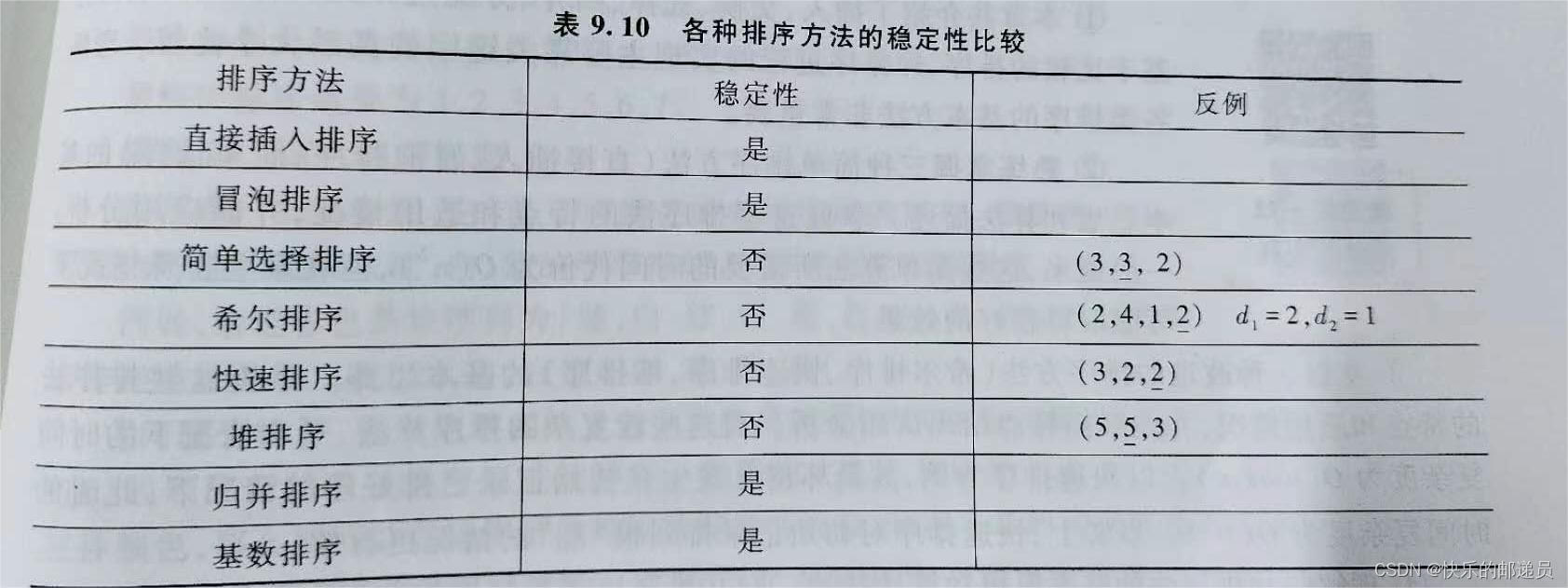
稳定的排序:直接插入排序、冒泡排序、归并排序、基数排序
2.?排序方法中,从未排序序列中依次取出元素与已排序序列中的元素进行比较,将其放入已排序序列的正确位置的方法称为:(A)
A.插入排序
B.选择排序
C.快速排序
D.归并排序
3.对N个记录进行快速排序,在最坏的情况下,其时间复杂度是:(C)
A.O(N)
B.O(NlogN)
C.O(N2)
D.O(N2logN)
4.对N个记录进行堆排序,最坏的情况下时间复杂度是:(C)
A.O(logN)
B.O(N)
C.O(NlogN)
D.O(N2)
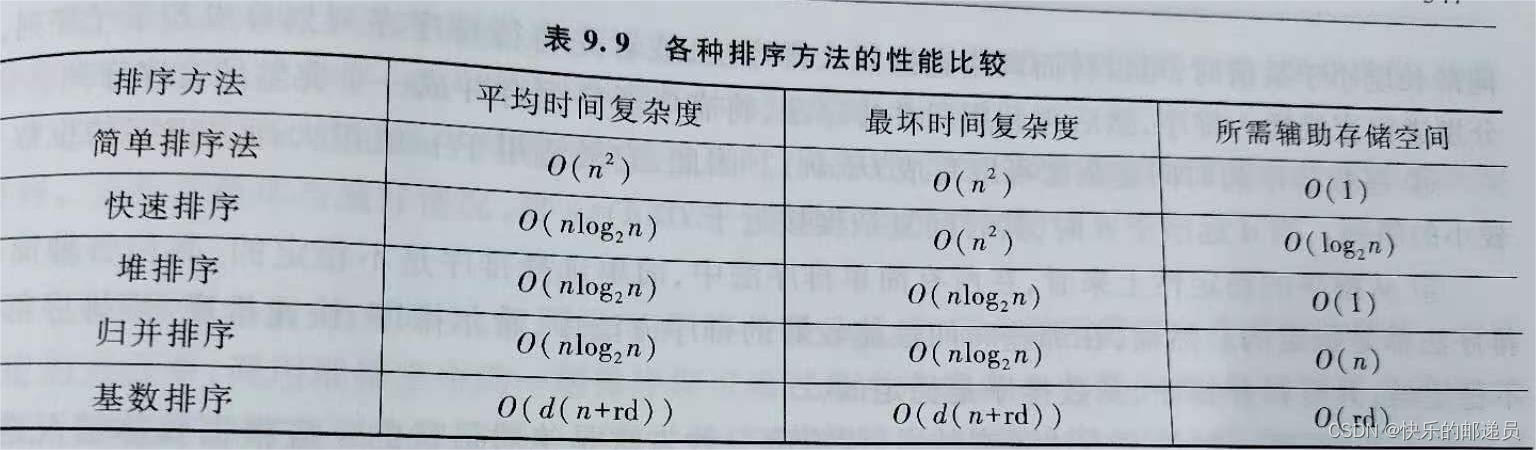
5。有组记录的排序码为{ 46,79,56,38,40,84 },则利用堆排序的方法建立的初始堆为:(D)
A.79,46,56,38,40,80
B.84,79,56,46,40,38
C.84,56,79,40,46,38
D.84,79,56,38,40,46
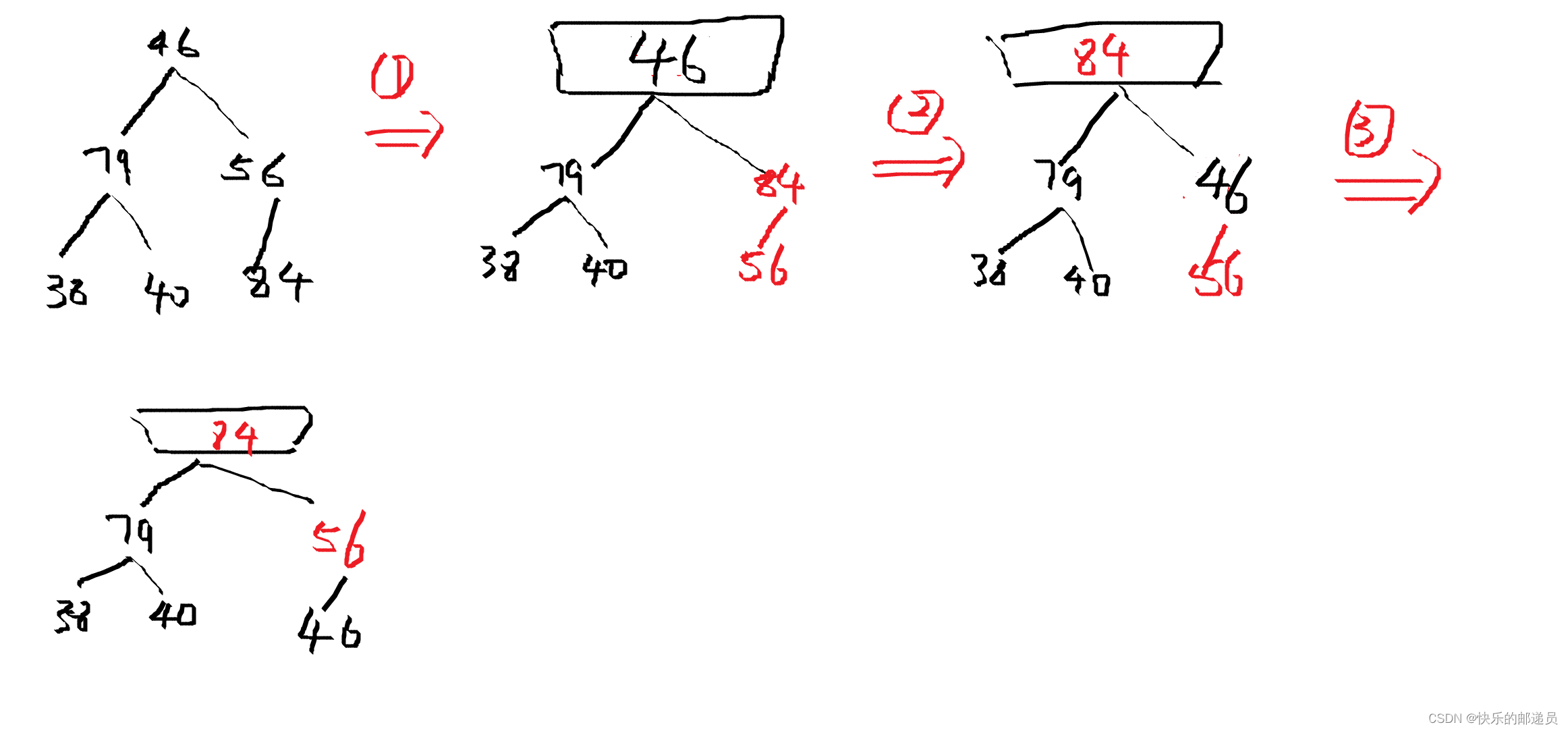
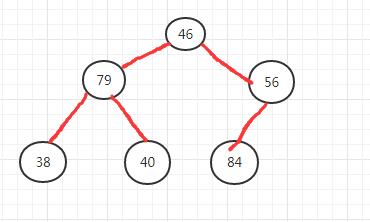
堆排序是基于最大堆来实现的。
- 将待排序的数据看作一棵完全二叉树,将第一个数据作为二叉树的根,从左至右依次填充二叉树。
- 对这棵完全二叉树进行调整建堆,即父节点不小于两个子节点为原则。
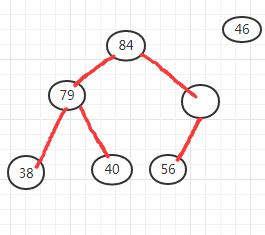
- 重建堆:将根节点46移出作为待调整节点,然后对根节点的左右子树重建堆。根据得出的树图来看左子树不变,右子树84和56交换位置。
- 从84和79选择较大的84同待调整的46做比较,将84上移到根节点。
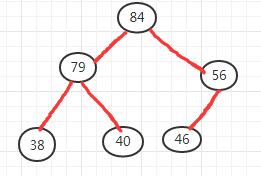
- 将56和待调整的46做比较,56上移到空节点处,46移到56位置处。
所以最终的初堆序列为:84,79,56,38,40,46
6.?有组记录的排序码为{46,79,56,38,40,84 },采用快速排序(以位于最左位置的对象为基准而)得到的第一次划分结果为:(D)
A.{38,46,79,56,40,84}
B.{38,79,56,46,40,84}
C.{38,46,56,79,40,84}
D.{40,38,46,56,79,84}

 ?
?
7.对于序列{ 49,38,65,97,76,13,27,50 },按由小到大进行排序,下面哪一个是初始步长为4的希尔排序法第一趟的结果?(B)
A.13,27,38,49,50,65,76,97
B.49,13,27,50,76,38,65,97
C.49,76,65,13,27,50,97,38
D.97,76,65,50,49,38,27,13
长度为4的序列:
{49,76} {38,13} {65,27} {97,50}
从小到大进行排序:
{49,76} {13,38} {27,65} {50,97}
所以最后第一趟排序,先输出左半部分,再输出右半部分
49 13 27 50 76 38 65 97?
8.下列排序算法中,时间复杂度不受数据初始状态影响,恒为O(NlogN)的是:(C)
A.冒泡排序
B.直接选择排序
C.堆排序
D.快速排序
9.设有1000个元素的有序序列,如果用二分插入排序再插入一个元素,则最大比较次数是(D)
A.1000
B.999
C.500
D.10
二分插入排序:最好情况:o(nlog(n))? ?最坏情况(o(n*n))
log2(10000)+1=10
2^10=1024
10.对于7个数进行冒泡排序,最坏情况下需要进行的比较次数为(C)
A.7
B.14
C.21
D.49
n*(n-1)/2;
即:7*6/2=21
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!