最小二乘直线拟合算法

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：最小二乘直线拟合

背景

ptb认证

ptb是对几何体拟合算法的认证。

主要涉及3D直线，3D圆，平面，球，圆柱，锥。

官方会给出点云信息，由用户将拟合结果上传到官方服务器进行对比答案，返回结果。

拟合有很多种度量标准，不同的标准出来的答案可能不完全精确。所以，要通过认证必须用官方给定的度量方法，具体可以参考论文。

认证精度要求

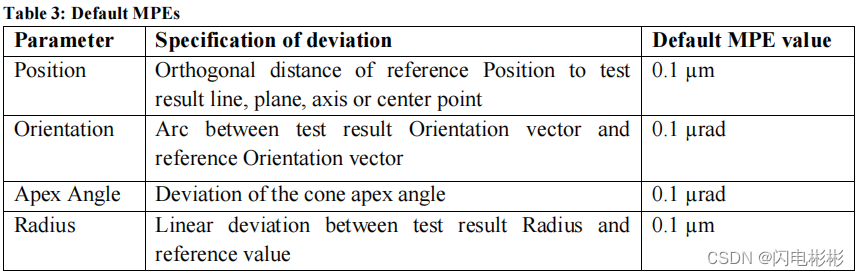
对于位置类型，比如圆心，直线的点等，误差不能超过0.0001mm。

对于角度，比如圆锥的开角，误差不能超过0.0000001rad。

对于方向，与标准值夹角不能直过0.0000001rad。

对于半径，误差不能超过0.0001mm。

学习资料

论文资料
Forbes, Alistair B.: Least-squares best fit geometric elements, NPL Report DITC 140/89 , ISSN
0262-5369, 40 pages, revised edition, 1991

由NPL发表。里面介绍了所有ptb认证的拟合算法。

直线拟合输入和输出要求

输入

1. 8到50个点，全部采样自直线上。
2. 每个点3个坐标，坐标精确到小数点后面20位。
3. 坐标单位是mm, 范围[-500mm, 500mm]。

tips
输入虽然是严格来自直线，但是由于浮点表示，记录的值和真实值始终是有微小的误差，点云到拟合直线的距离不可能完全为0。

输出

1. 直线上1点p，用三个坐标表示。
2. 直线方向k，用三个坐标表示，需要单位化。

精度要求

1. p点到标准直线距离不能超过0.0001mm。
2. k与标准法向的夹角不能超过0.0000001rad。

直线优化标函数

根据论文，直线拟合转化成数学表示如下：

直线参数化表示

1. 直线上1点X0 = (x0, y0, z0)。
2. 方向单位向量A=(a,b,c)。

点到直线距离

第i个点 pi(xi, yi, zi)。

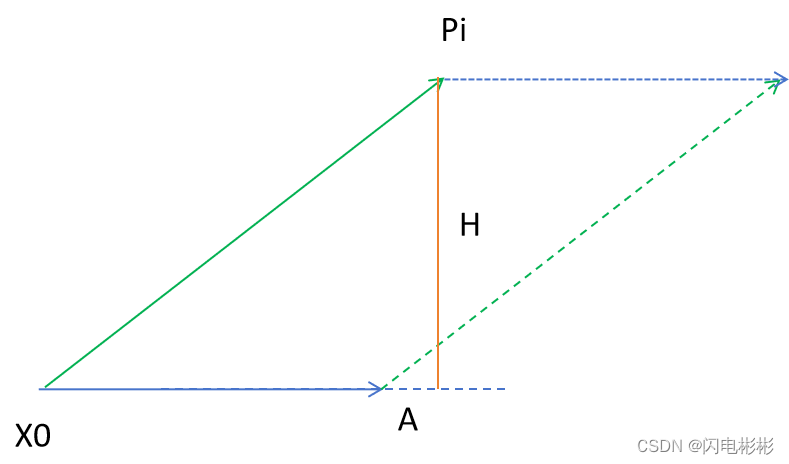
可以根据叉乘长度为面积，面积又等于底乘高，点到直线的距离是叉乘结果除以底。底是单位向量。

$d_i=H=\frac{\Vert (p_i?X_0)\times A\Vert }{\Vert A\Vert }$

$d_i=\Vert (p_i?X_0)\times A\Vert$

展开一下：

$d_i=\sqrt{(u_i^2+v_i^2+w_i^2)}$

$u_i=c(y_i?y_0)?b(z_i?z_0)$

$v_i=a(z_i?z_0)?c(x_i?x_0)$

$w_i=b(x_i?x_0)?a(y_i?y_0)$

最小二乘优化能量方程

能量方程 $E=f(X0,A)=\sum _1^n{d}_i^2$

上式是一个6元二次函数中，X0, A是未知量，拟合直线的过程也可以理解为优化X0, A使得方程E最小。

上述方程中向量的值不确定，所以并不好解，一般直线拟合会对协方差矩阵求特征向量来得到直线方程，具体可以看下面的主成分分析法。

拟合&测试基类设计

基类主要放一些公共方法和规定具体实现类要实现的算法。

具体在调用时，都用基类为载体，减少代码量。

拟合基类

#include <Eigen/Core>
#include <vector>
#include "GeometryTypes.h"


namespace Fitting {
	using Matrix = Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>;
	/* getCenter
		获取点云中心
	 */
	Eigen::Vector3d getCenter(const std::vector<Eigen::Vector3d>& points);

	/* moveCenter
	* 将中心移至0点
	*/
	void moveCenter(const Eigen::Vector3d center, std::vector<Eigen::Vector3d>& points);

	/* getRotationByOrient(Eigen::Vector3d orient);
	* 返回一个旋转矩阵使得向量与Z轴平行
	*/ 
	Eigen::Matrix3d getRotationByOrient(Eigen::Vector3d orient);
	class FittingBase {
	protected:
		Eigen::Matrix3d U;
		std::vector<Eigen::Vector3d> transPoints;
		/* Jacobi
		* 构造jacobi矩阵
		*/
		virtual Matrix Jacobi(const std::vector<Eigen::Vector3d> &points)=0;
		
		/* findNext
		*	迭代1次得到解delta
		*/
		Eigen::VectorXd findNext(const std::vector<Eigen::Vector3d>& points);

		/* beforHook
		* 每次迭代前的准备工作
		*/
		virtual void beforHook(Eigen::VectorXd& a0, const std::vector<Eigen::Vector3d>& points)=0;
		
		/* afterHook
		* 迭代后更新答案
		*/
		virtual void afterHook(const Eigen::VectorXd& xp)=0;

		
		/* 获取 d数组
		*/
		virtual Eigen::VectorXd getDArray(const std::vector<Eigen::Vector3d>& points)=0;
		 
		// GetInitFit 返回是否拟合成功
		virtual bool GetInitFit(const std::vector<Eigen::Vector3d>& points)=0;
		// iteration
		double iteration(const std::vector<Eigen::Vector3d>& points);

		/* F
		* 距离函数
		*/
		virtual double F(const Eigen::Vector3d& p)=0;

		/* 获取 最小二乘残差
		*/
		virtual double  GetError(const std::vector<Eigen::Vector3d>& points) = 0;
		/* 获取 结果
		*/
		virtual void Copy(void* ele) = 0;

	public:
		// Fitting
		double Fitting(const std::vector<Eigen::Vector3d>& points, void* ele);
	};
}

测试基类

namespace Fitting {
	const double POSITION_MAX_DST = 0.0001, ORIENTATION_MAX_DST = 0.0000001, ANGLE_MAX_DST = 0.0000001, RADIUS_MAX_DST = 0.0001;

	void writePoint(FILE *fp, const Point &p);
	void writeNumber(FILE *fp, double n);

	// 比较直线点是否一致
	bool lineCmp(const Eigen::Vector3d &vec1, const Point &p1, const Point &p2);
	bool lineCmp2D(const Eigen::Vector3d &vec1, const Point &p1, const Point &p2);
	// 比较半径
	bool radiusCmp(double r1, double r2);
	// 比较法向是否一致
	bool orientationCmp(const Eigen::Vector3d &vec1, const Eigen::Vector3d& vec2);
	bool orientationCmp2D(const Eigen::Vector3d &vec1, const Eigen::Vector3d& vec2);
	// 比较角度
	bool angleCmp(double angle1, double angle2);
	// 比较点位置
	bool positionCmp(const Point &p1, const Point &p2);

	/*
	测试基类
	*/
	class TestBase {
	protected:
		// 测试用例路径和文件名
		string suffixName, fileName;
		vector<Point> points;
	public:
		TestBase() {}
		TestBase(string _suffixName, string _fileName): suffixName(_suffixName), fileName(_fileName) {}
		void SetFile(string _suffixName, string _fileName);

		void readPoints();
		virtual double Fitting()=0;
		virtual bool JudgeAnswer(FILE* fp) = 0;
		virtual void ReadAnswer() = 0;
		virtual void SaveAnswer(FILE* fp) = 0;
	};

}

PCA主成分分析法

学习资料：
https://www.bilibili.com/video/BV1E5411E71z/?spm_id_from=333.337.search-card.all.click&vd_source=fb27f95f25902a2cc94d4d8e49f5f777

算法过程

1. 计算出所有点平均值 $centerid(\overline{x},\overline{y},\overline{z})$ , 作为直线上1点。
2. 构建矩阵$A=\left[\begin{array}{ccc}{x}_1?\overline{x}& y_1?\overline{y}& z_1?\overline{z}\\ x_2?\overline{x}& y_2?\overline{y}& z_2?\overline{z}\\ ...& ...& ...\\ x_n?\overline{x}& y_n?\overline{y}& z_n?\overline{z}\end{array}\right]$
3. 对矩阵A进行SVD分解，取右特征值矩阵最大特征值所对应列作为直线的法向。

代码实现

代码链接：https://gitcode.com/chenbb1989/3DAlgorithm/tree/master/CBB3DAlgorithm/Fitting
拟合代码

#include "FittingLinePCA.h"
#include "FittingBase.h"
#include <Eigen/Dense>

namespace Gauss {
	using namespace Fitting;
	double F(const Line& line, const Point& p) {
		return (p - line.BasePoint).cross(line.Orient).squaredNorm();
	}

	double  GetError(const Line& line, const std::vector<Eigen::Vector3d>& points) {
		double error = 0;
		for (auto& p : points) {
			error += F(line, p);
		}

		return error / points.size();
	}

	double FittingLinePCA::FittLine2D(const std::vector<Point>& points, Line2D& line) {
		return 0;
	}

	double FittingLinePCA::FittLine3D(const std::vector<Point>& points, Line& line) {
		auto center = Fitting::getCenter(points);
		std::vector<Point> copyPoints = points;
		Fitting::moveCenter(center, copyPoints);

		Eigen::MatrixX3d A(copyPoints.size(), 3);

		for (int i = 0; i < copyPoints.size(); ++i) {
			A.block<1, 3>(i, 0) = copyPoints[i];
		}
		Eigen::JacobiSVD<Eigen::MatrixX3d> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);
		line.Orient = svd.matrixV().block<3, 1>(0, 0);
		line.BasePoint = center;

		return GetError(line, points);
	}
}

测试代码

	void TestAllCase() {
		string caseDir = "D:/selfad/alg_and_graph/3DAlgorithm/CBB3DAlgorithm/Fitting/gauss/";

		FILE* caseList = fopen((caseDir+"data/kind.txt").c_str(), "r");
		char baseID[100], kind[100];
		FILE* testResult = fopen((caseDir + "fitting_result/result.txt").c_str(), "w");
		while (fscanf(caseList, "%s", baseID) != EOF) {
			strcpy(kind, baseID + 4);
			baseID[3] = 0;
			/*puts(baseID);
			puts(kind);*/

			TestBase* testLogic = getTestObj(kind);
			if (testLogic == NULL)continue;
			fprintf(testResult, "%s : %s : ", baseID, kind);

			testLogic->SetFile(caseDir, baseID);


			testLogic->readPoints();
			testLogic->Fitting();
			FILE* ansfp = fopen((caseDir + "fitting_result/" + baseID + ".txt").c_str(), "w");
			testLogic->SaveAnswer(ansfp);
			
			fprintf(testResult, "%s\n", testLogic->JudgeAnswer(NULL)?"pass":"failed");

			fclose(ansfp);
			delete testLogic;
		}

		fclose(caseList);
		fclose(testResult);
		puts("TEST COMPLETE");
	}

测试结果

https://gitcode.com/chenbb1989/3DAlgorithm/blob/master/CBB3DAlgorithm/Fitting/gauss/fitting_result/result.txt

b01 : LINE_3D : pass
b02 : LINE_3D : pass
b03 : LINE_3D : pass
b04 : LINE_3D : pass

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。