贝叶斯分类器（公式推导+举例应用）

引言

在机器学习的世界中，有一类强大而受欢迎的算法——贝叶斯分类器，它倚仗着贝叶斯定理和朴素的独立性假设，成为解决分类问题的得力工具。这种算法的独特之处在于其对概率的建模，使得它在面对不确定性和大规模特征空间时表现卓越。

本文将深入探讨贝叶斯分类器，首先通过详细的公式推导带你走进其内部机制，随后通过实际案例展示其在各个领域的广泛应用。

贝叶斯决策论

贝叶斯决策论是一种基于概率论和决策理论的决策框架，其核心思想是通过最大化期望效用来做出最优的决策。该理论的基础是贝叶斯定理，它将不确定性引入决策过程中，特别适用于需要考虑不确定性因素的问题。

假设有$N$种可能的类别标记，即 y = { c 1 , c 2 , . . . , c N } y=\{c_1,c_2,...,c_N\} y={c1?,c2?,...,cN?}，${\lambda }_{ij}$是将一个真实标记为$c_j$的样本误分类为$c_i$所产生的损失。基于后验概率$P(c_i|x)$可获得将样本$x$分类为$c_i$所产生的期望损失，即样本$x$上的条件风险：
$$R(c_i|x)=\sum _{j=1}^N{\lambda }_{ij}P(c_j|x)\text{\hspace{1em}(1)}$$

我们的任务是寻找一个判定准则$h:\chi ?y$以最小化总体风险：
$$R(h)=\mathbb{E}[R(h(x)|x)]\text{\hspace{1em}(2)}$$
其中$\mathbb{E}$表示期望值。显然，对于每个样本$x$，若$h$能最小化条件风险$R(h(x)|x)$，则总体的$R(h)$也将会被最小化。

贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险$R(c|x)$最小的类别标记，即：
$$h^{?}(x)=ar{g}_{c\in y}minR(c|x)\text{\hspace{1em}(3)}$$

此时，$h^{?}$称为贝叶斯最优分类器，与之对应的总体风险$R(h^{?})$称为贝叶斯风险。$1?R(h^{?})$反映了分类器所能达到的最好性能。

具体来说，若目标是最小化分类错误率，则误判损失${\lambda }_{ij}$可写为：
$${\lambda }_{ij}=\{\begin{array}{l}0,ifi=j\\ 1,otherwise\end{array}\text{\hspace{1em}(4)}$$
此时条件风险：
$$R(c|x)=1?P(c|x)\text{\hspace{1em}(5)}$$

于是最小化分类错误率的贝叶斯分类器为：
$$h^{?}(x)=ar{g}_{c\in y}maxP(c|x)\text{\hspace{1em}(6)}$$

即对每个样本$x$，选择能使后验概率$P(c|x)$最大的类别标记。

然而在现实任务中，我们很难得到后验概率$P(c|x)$。

自此我们有两种策略：

• 判别式模型：给定$x$，可通过直接建模$P(c|x)$来预测$c$。
• 生成式模型：对联合概率分布$P(x,c)$建模，然后再由此获得$P(c|x)$。

显然对于生成式模型来说，需考虑：
$$P(c|x)=\frac{P(x,c)}{P(x)}\text{\hspace{1em}(7)}$$

基于贝叶斯定理，$P(c|x)$可写为：
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}\text{\hspace{1em}(8)}$$

因此估计$P(c|x)$的问题就转化为如何基于训练数据$D$来估计先验概率$P(c)$和似然$P(x|c)$。

先验概率和后验概率

先验概率（Prior Probability）

先验概率是在考虑任何观测数据之前，对事件的概率进行估计。它是基于以往经验、领域知识或其他信息得出的概率。符号通常表示为$P(A)$，其中$A$是事件。先验概率反映了在考虑新观测数据之前我们对事件的信念。

后验概率（Posterior Probability）

后验概率是在考虑了新的观测数据之后，对事件的概率进行修正的概率。它是基于先验概率和新观测数据的联合影响得出的概率，使用贝叶斯定理计算。符号通常表示为$P(A|B)$，其中$A$是事件，$B$是观测数据。后验概率反映了在获得新信息后我们对事件的修正信念。

让我们通过一个简单的例子来生动形象地描述先验概率和后验概率的概念。
场景：病人的健康检查

• 先验概率的理解： 假设有一个医生，他的病人群体中，有 10% 的人患有某种疾病（事件 $A$）。这个 10% 的患病率是基于医生以往的经验和病历统计得到的。在这里，患病率 10% 就是先验概率$P(A)$。
• **后验概率的理解：**现在，该医生对一位新的病人进行了检查，得到了一些特定的症状（事件 $B$）。在这个特定的病人身上，这些症状出现的概率是多少呢？这就是后验概率$P(A|B)$。

使用贝叶斯定理，医生可以更新他的信念。假设在已知患病率为 10% 的情况下，症状出现的概率为 80%（这是似然度$P(B|A)$)，而病人患有该疾病的概率就可以通过贝叶斯定理计算。
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
这里，$P(B)$表示症状出现的概率，可以通过考虑所有可能情况来计算。例如，患病且出现症状的情况和不患病但出现症状的情况。
医生通过这个计算，得到了在考虑了新的症状后，病人患有该疾病的后验概率。这个后验概率可以帮助医生更准确地评估病人的健康状况，这就是后验概率的概念。

极大似然估计

极大似然估计（Maximum Likelihood Estimation，简称MLE）是一种常用的参数估计方法，用于估计统计模型中的参数。该方法基于观测到的数据，寻找使得观测到这些数据的概率最大的模型参数。

具体的，记关于类别$c$的类条件概率为$P(x|c)$，假设$P(x|c)$具有确定的形式且被参数向量${\theta }_c$唯一确定，则我们的任务就是利用训练集$D$估计参数${\theta }_c$。为明确起见，我们将$P(x|c)$记为$P(x|{\theta }_c)$。

令$D_c$表示训练集$D$中的第三$c$类样本组成的集合，假设他们都是独立同分布的，则参数${\theta }_c$对于数据集$D_c$的似然是：
$$P(D_c|{\theta }_c)=\prod _{x\in D_c}P(x|{\theta }_c)\text{\hspace{1em}(9)}$$

对${\theta }_c$进行极大似然估计，就是去寻找能最大化似然$P(D_c|{\theta }_c)$的参数值${\hat{\theta }}_c$。从直观上讲，极大似然估计就是寻找在所有取值中，最大的一个${\hat{\theta }}_c$。

式（9）中连乘会导致下溢，通常使用对数似然：
$$\begin{array}{rl}LL({\theta }_c)& =logP(D_c|{\theta }_c)\\ & =\sum _{x\in D_c}logP(x|{\theta }_c)\end{array}\text{\hspace{1em}(10)}$$

此时的参数${\theta }_c$的极大似然估计${\hat{\theta }}_c$为：
$$\begin{array}{rl}{\hat{\theta }}_c=& \underset{{\theta }_c}{\arg }maxLL({\theta }_c)\end{array}\text{\hspace{1em}(11)}$$

朴素贝叶斯分类器

朴素贝叶斯分类器是一种基于贝叶斯定理的分类算法，它假设特征之间是相互独立的（朴素贝叶斯的"朴素"就体现在这里），并且使用了一些概率统计的方法进行分类。它广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。

基于属性条件独立性假设，式（8）可重写为：
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod _{i=1}^{d}P(x_i|c)\text{\hspace{1em}(12)}$$

其中$d$为属性数目，$x_i$为$x$在第$i$个属性上的取值。

由于对于所有类别来说$P(x)$相同，因此基于式（6）的贝叶斯判定准则有：
$$\begin{array}{rl}{h}_{nb}(x)=& \underset{c\in y}{\arg }maxP(c)\prod _{i=1}^{d}P(x_i|c)\end{array}\text{\hspace{1em}(13)}$$

这就是朴素贝叶斯分类器的表达式。

令$D_c$表示训练集$D$中第$c$类样本组成的集合，若有充足的独立同分布样本，则可容易地估计出类先验概率：
$$P(c)=\frac{|D_c|}{|D|}\text{\hspace{1em}(14)}$$

现在我们估计似然$P(x_i|c)$：

• 对于离散数据而言：令$D_{c,x_i}$表示$D_c$中的第$i$个属性上取值为$x_I$的样本组成的集合，则条件概率$P(x_i|c)$可估计为：
  $$P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}\text{\hspace{1em}(15)}$$

• 对于连续数据而言：可以考虑概率密度，假定$p(x_i,c)～N({\mu }_{c,i},{\sigma }_{c,i}^2)$，即$p(x_i,c)$服从均值为${\mu }_{c,i}$，方差为${\sigma }_{c,i}^2$的正态分布，则有：
  $$p(x_i,c)=\frac{1}{\sqrt{2\pi }{\sigma }_{c,i}}{e}^{?\frac{(x_i?{\mu }_{c,i}{)}^2}{2{\sigma }_{c,i}^2}}\text{\hspace{1em}(16)}$$

朴素贝叶斯分类器的优点与缺点

优点

• 朴素贝叶斯算法简单，易于实现。
• 在处理大规模数据集时表现良好。
• 在特征之间相对独立的情况下，效果良好。

缺点

• 对于特征之间相关性较强的数据，朴素贝叶斯可能表现不佳。
• 对于缺失数据的处理相对较为复杂。

总体而言，朴素贝叶斯分类器在许多实际应用中表现良好，特别是在文本分类等领域。

总结

在本文中，我们深入探讨了贝叶斯分类器及其相关概念。首先，我们通过详细的公式推导介绍了贝叶斯决策论，阐述了其基于概率和决策理论的决策框架。接着，我们讨论了贝叶斯定理的先验概率和后验概率，通过生动的例子说明了这两个概念的重要性和应用场景。

随后，我们转向了极大似然估计，解释了在统计模型中使用观测数据来估计参数的方法。通过推导极大似然估计的基本原理，我们理解了其在模型参数估计中的重要性。

最后，我们详细介绍了朴素贝叶斯分类器，阐述了其基于贝叶斯定理和属性条件独立性假设的工作原理。我们还探讨了朴素贝叶斯分类器的优点和缺点，以及其在实际应用中的广泛使用，特别是在文本分类等领域。

总体而言，贝叶斯分类器作为一种强大而灵活的机器学习算法，在不同领域展现出了卓越的性能。通过深入了解其原理和应用，我们能够更好地理解和利用这一算法来解决实际问题。希望本文能够为读者提供清晰的认识，并激发对贝叶斯分类器更深层次研究的兴趣。

实验分析

判断一封邮件是否为垃圾邮件。

import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, classification_report

# 读入数据集
df = pd.read_csv('data/spam_or_not_spam.csv')

训练朴素贝叶斯分类器

# 先去除包含 NaN 值的行
df = df.dropna(subset=['email', 'label'])

X = df['email']
y = df['label']

# 文本转词袋模型
vectorizer = CountVectorizer(stop_words='english')
X = vectorizer.fit_transform(X)

# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练朴素贝叶斯分类器
nb_classifier = MultinomialNB()
nb_classifier.fit(X_train, y_train)

# 预测
y_pred = nb_classifier.predict(X_test)

import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

# 模型评估
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy}")
print("Classification Report:\n", report)

# 设置中文字体
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
plt.rcParams['font.sans-serif'] = ['SimSun']  # 设置字体为宋体

# 生成混淆矩阵
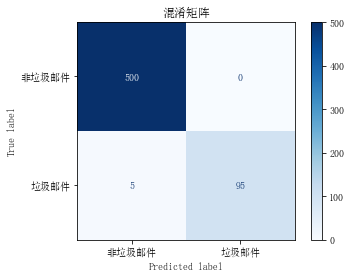
cm = confusion_matrix(y_test, y_pred)

# 绘制混淆矩阵图
plt.figure(figsize=(8, 6))
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=['非垃圾邮件', '垃圾邮件'])
disp.plot(cmap=plt.cm.Blues)
plt.title('混淆矩阵', fontproperties=font)
plt.show()

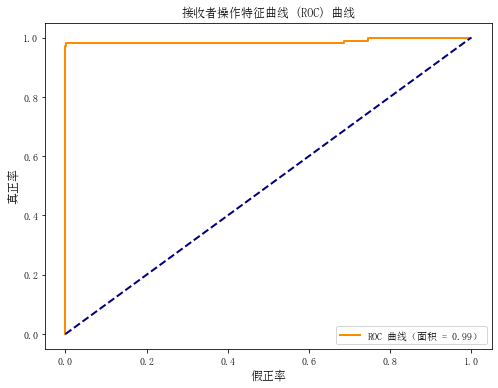
# 生成 ROC 曲线
y_probs = nb_classifier.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(y_test, y_probs)
roc_auc = auc(fpr, tpr)

# 绘制 ROC 曲线图
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC 曲线（面积 = {:.2f}）'.format(roc_auc))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('假正率', fontproperties=font)
plt.ylabel('真正率', fontproperties=font)
plt.title('接收者操作特征曲线 (ROC) 曲线', fontproperties=font)
plt.legend(loc='lower right')
plt.show()

Accuracy: 0.9916666666666667
Classification Report:
               precision    recall  f1-score   support

           0       0.99      1.00      1.00       500
           1       1.00      0.95      0.97       100

    accuracy                           0.99       600
   macro avg       1.00      0.97      0.98       600
weighted avg       0.99      0.99      0.99       600

1. 准确度（Accuracy）： 0.9917，表示模型在整体上正确预测的比例。这是一个很高的准确度，说明模型在测试数据上的表现非常好。

2. 分类报告（Classification Report）：

• 对于类别 0（非垃圾邮件）：
  • 精确度（Precision）：0.99，表示在所有模型预测为非垃圾邮件的样本中，实际上有 99% 是正确的。
  • 召回率（Recall）：1.00，表示在所有实际非垃圾邮件的样本中，模型成功预测的比例为 100%。
  • F1 分数（F1-score）：1.00，是精确度和召回率的调和平均值，综合考虑了两者。
  • 支持度（Support）：500，表示测试集中实际为非垃圾邮件的样本数量。
• 对于类别 1（垃圾邮件）：
  • 精确度：1.00，表示在所有模型预测为垃圾邮件的样本中，实际上有 100% 是正确的。
  • 召回率：0.95，表示在所有实际垃圾邮件的样本中，模型成功预测的比例为 95%。
  • F1 分数：0.97，是精确度和召回率的调和平均值，综合考虑了两者。
  • 支持度：100，表示测试集中实际为垃圾邮件的样本数量。

3. 加权平均（weighted avg）： 这是对各类别指标进行加权平均，考虑到每个类别的支持度。在这里，加权平均的准确度、精确度、召回率和 F1 分数都达到了 0.99。

4. 宏平均（macro avg）： 这是对各类别指标取平均，不考虑各类别的支持度。在这里，宏平均的准确度、精确度、召回率和 F1 分数分别为 1.00、0.97、1.00 和 0.98。

总体来说，模型在非垃圾邮件的预测上表现非常好，而在垃圾邮件的预测上稍微有些降低，主要体现在垃圾邮件的召回率上。综合考虑各指标，模型在整体上仍然表现出色。