neuq-acm预备队训练week 9 P8604 [蓝桥杯 2013 国 C] 危险系数
发布时间:2023年12月18日
题目背景
抗日战争时期,冀中平原的地道战曾发挥重要作用。
题目限制

题目描述
地道的多个站点间有通道连接,形成了庞大的网络。但也有隐患,当敌人发现了某个站点后,其它站点间可能因此会失去联系。
我们来定义一个危险系数 DF(x,y):
对于两个站点?x?和 y(x!=y),?如果能找到一个站点?z,当?z?被敌人破坏后,x?和?y?不连通,那么我们称?z?为关于?x,y?的关键点。相应的,对于任意一对站点?x?和?y,危险系数 DF(x,y)?就表示为这两点之间的关键点个数。
本题的任务是:已知网络结构,求两站点之间的危险系数。
输入格式
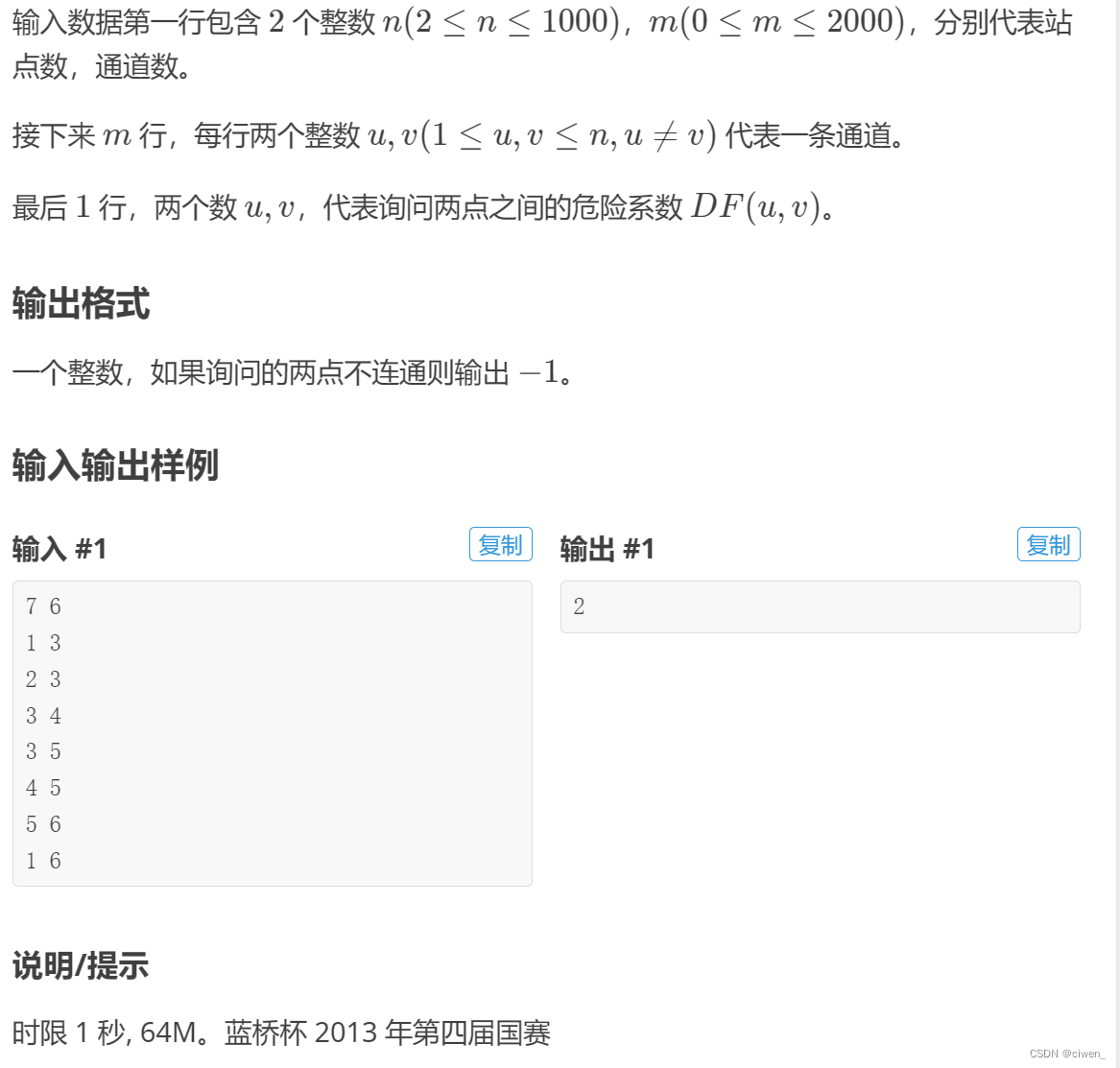
解题思路
这题可以用dfs来解,具体看代码
AC代码
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,ans,cnt[1010],sum;
bool b[1010],a[1010][1010];
void dfs(int N);
int main()
{
scanf("%d%d",&n,&m);
while(m--)
{
scanf("%d%d",&u,&v);
a[u][v]=a[v][u]=1;//无向,令u到v和v到u为1
}
scanf("%d%d",&u,&v);
dfs(u);
if(sum>0)
{
for(int i=1;i<=n;i++)
if(cnt[i]==sum) //如果这个点被走过的总次数与路径总数相等(必经点)
ans++; //那么删去这个点起点与终点间一定不连通。
printf("%d",ans-1); //因为终点也被算在内,所以总危险系数要减去起点的1。
}
else
printf("-1"); //如果无路径连通则输出-1
return 0;
}
void dfs(int N)
{
if(N==v) //如果到终点
{
sum++; //路径总数加一
for(int i=1;i<=n;i++)
if(b[i]==1)
cnt[i]++;//每个被走过的点,被走总次数加一
}
else
{
for(int i=1;i<=n;i++)
if(a[N][i]==1&&b[i]==0)//如果未被走过
{
b[i]=1;//标记
dfs(i);
b[i]=0;//回溯
}
}
}
文章来源:https://blog.csdn.net/ciwen_/article/details/135050241
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 亚马逊圣诞关键词怎么选?圣诞节促销活动有哪些?——站斧浏览器
- C语言进阶指南(22)——文件管理函数
- 重装系统之----Rufus创建UEFI启动盘
- Codeforces Round 646 (Div. 2) C. Game On Leaves
- Windows RPC运行时漏洞事后总结
- 浅析CXL P2P DMA加速数据传输拥堵问题的解决方案
- react hooks
- vue-springboot基于java的社区志愿者活动信息管理系统 e2y4d
- XETUX软件 dynamiccontent.properties.xhtml RCE漏洞复现
- 1162字符串逆序