计算机图形学理论(2):网格表达
发布时间:2023年12月20日
为什么网格表达很重要?
在上一篇文章中,我们介绍了多边形网格的概念。多边形网格是多边形(通常是三角形)的集合。
让我们考虑一个复杂的现实世界对象,这个对象由上百万个三角形组成,然后在我们的屏幕上进行渲染,这个计算量将非常庞大!
所以我们应该在尽可能保持模型质量的同时简化模型。
为了获得网格的最佳表示,我们需要满足一些特点:
- 数据紧凑
- 通用
- 计算简单
- 高效率
在我们开始之前,先来看一个网格优化的示例:
[边塌陷]
在很多情况下,边对于表示整个对象是没有用的,因为它不必要地生成了额外的三角形。通过删除多边形中的最短边,我们可以减少三角形的数量。

我们需要:边的列表、每条边关联的三角形、顶点信息、每个顶点关联的三角形
网格数据结构
出于通用性考虑,我们最好满足以下条件:
- 多边形汤(polygon soup)
- 仅包含三角形
- 二维流形(2-manifold,每条边少于两个三角形)
- 可定向(逆时针方向连接)
- 封闭(无边界)
什么是二维流形?
在百度百科上的解释比较难以理解,可以看下面的例子:
可以看到两个红色顶点之间的连线并不满足“每条边仅与一个或两个面相关”,是与三个面相关,那么这个就是个非流形几何。
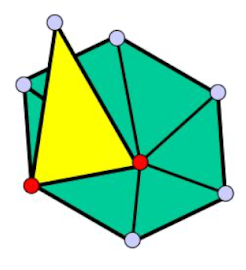
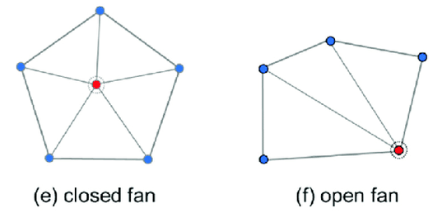
二维流形应满足与顶点相接的面形成封闭或开放的扇形:
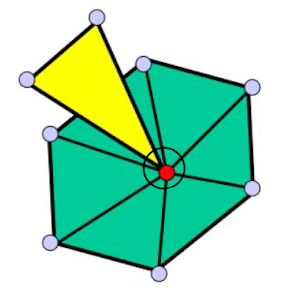
但是下面的网格与另一个三角形相关联,没有共享边,所以它不是二维流形。
三角形网格
三角网是 3D 空间中的一堆三角形连接在一起形成一个表面。
表示三角形网格的方法
- 单独的三角形
看下图中的红色菱形,由两个三角形拼接,这个菱形会占用72个字节。float[triangle_index][3][3] :2 个三角形 * 每个三角形 3 个顶点 * 每个顶点 3 个坐标 * 4byte(float)
由于三角形是独立的,因此顶点列表中存在重复项。简单地说,存储有关三角形的信息并不紧凑,但足以渲染网格。 (也满足二维流形形式)
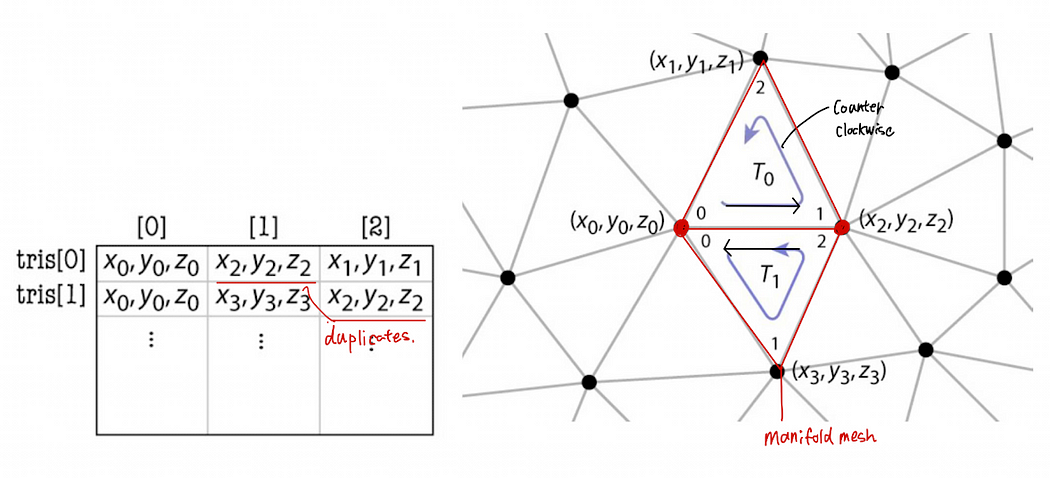
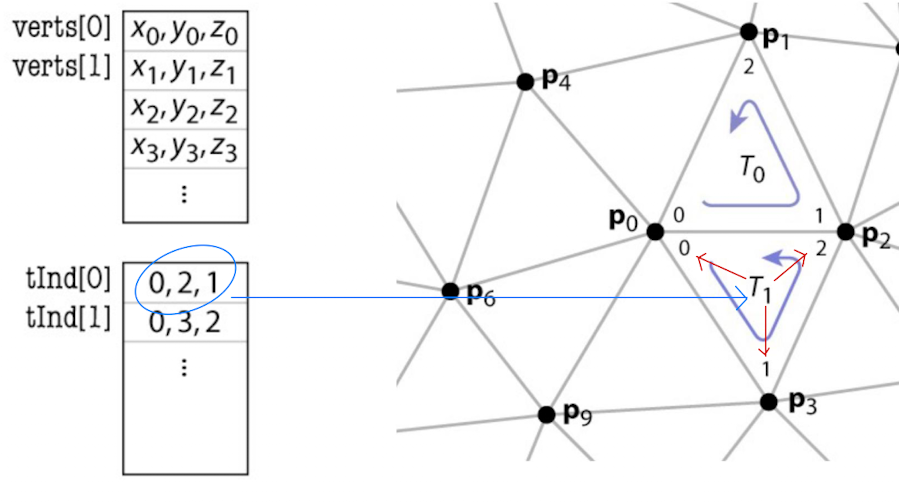
- 索引三角形集(共享顶点)
通过这种方式,我们可以将每个顶点存储一次,并且每个三角形都指向它的三个顶点。
我们可以减少内存使用,因为信息是根据三角形索引的。
但计算法线效率不高,因为它需要遍历相邻节点。
Triangle {
Vertex vertex[3];
}
Vertex {
float position[3];
}
Mesh {
float verts[number of vertices][3]; // 存储每个顶点的坐标
int tInd[number of triangles][3]; // 存储每个三角形的顶点索引
}
- 三角带和三角扇(压缩方案)
- 三角形-邻接数据结构(邻接查询)
- 翼边数据结构(通用多边形网格)
文章来源:https://blog.csdn.net/u013929284/article/details/135105829
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 符合国际权威安全标准的 KillDisk Industrial System 磁盘擦除设备
- 基于ssm+vue服装商城购物系统
- 【深度学习】因果推断与机器学习的高级实践 | 数学建模
- 解决Electron中WebView加载部分HTTPS页面白屏的方法
- Jmeter事务控制器&聚合报告
- 浅谈表达式解析
- VR全景技术如何应用在城市发展,助力城市宣传展示
- 构建高效网络爬虫:代理IP池的建立与维护方法
- STM32F407-14.3.10-表73具有有断路功能的互补通道OCx和OCxN的输出控制位-1x001
- 数字IC实战后端项目| 必须掌握的28个SoC低功耗项目经验!