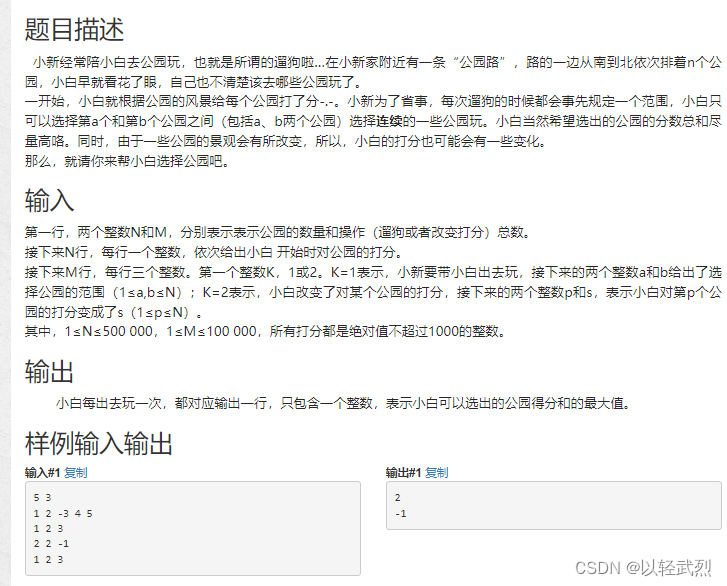
3375 小白逛公园

线段树的题啊……
还有输入中a可能大于b，要判断并交换。
这里我们用到了一种分治的思想
所以我们可以用这个结构体来储存一个区间
struct node
{
int left,right,maxv,sum;
}
其中left表示从左端点向右能达到的最大值
right表示从右端点到右所能达到的最大值
maxv就是我们要求的 即整个区间中能达到的最大连续和值
sum自然就是所有区间内所有数的和了
在最大连续子序列的和中
我们有动态规划好写+O(n)的算法
所以有的时候就忽略了我们的O(nlogn)的分治算法
我们看这么几个式子即renew函数更新节点的附加信息的函数
tree[o].sum=tree[o<<1].sum+tree[o<<1|1].sum;
tree[o].left=max(tree[o<<1].left,tree[o<<1].sum+tree[o<<1|1].left);
tree[o].right=max(tree[o<<1|1].right,tree[o<<1|1].sum+tree[o<<1].right);
tree[o].maxv=max(tree[o<<1].right+tree[o<<1|1].left,max(tree[o<<1].maxv,tree[o<<1|1].maxv));
第一个sum不言而喻地球人都知道
第二个left我们可以知道是要从左端点向右
那么我们分治分成两半 一定有要么是左半端点向右延伸没有到达中点
要么是左端端点延伸到达了右部分 所以这个时候肯定就是选取了全部的左边加上右端的left
第三个也是一样的道理咯 这里就不赘说了
第四个maxv我们就是和O(nlogn)算法的思路一样了
我们知道一个最大连续和的子序列 要么是左半段的最大和 要么就是右半段的最大和
要么就是横跨左右的最大和
那么我们对应的就是tree[o<<1].maxv tree[o<<1|1].maxv tree[o<<1].right+tree[o<<1|1].left
然后就取下最大值就好了
这样我们就完成了节点的值的维护方法咯
那么我们就可以用线段树来解决一个个区间问题了
这个因为打分是只改变一个的
所以就是简单的单点修改问题OTZ
然后直接狂撸就好了
ORZ%%%窝好弱啊

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int MAXN=500010;
struct node
{
    int left,right,maxv,sum;
}tree[MAXN<<2];
int n,m;
void renew(int o)
{
    tree[o].sum=tree[o<<1].sum+tree[o<<1|1].sum;
    tree[o].left=max(tree[o<<1].left,tree[o<<1].sum+tree[o<<1|1].left);
    tree[o].right=max(tree[o<<1|1].right,tree[o<<1|1].sum+tree[o<<1].right);
    tree[o].maxv=max(tree[o<<1].right+tree[o<<1|1].left,max(tree[o<<1].maxv,tree[o<<1|1].maxv));
}
void change(int o,int l,int r,int a,int c)//c为修改的值,a是要单点修改的点，o节点编号,l,r对应节点区间
{
    if(l==r)
    {
        tree[o].left=tree[o].right=tree[o].maxv=tree[o].sum=c;
        return;
    }
    int mid=(l+r)>>1;
    if(a<=mid)
        change(o<<1,l,mid,a,c);
    else
        change(o<<1|1,mid+1,r,a,c);
    renew(o);
}
node query(int o,int l,int r,int a,int b)//o节点编号,l r是节点对应区间,a,b为要查找的区间
{
    if(a<=l&&b>=r) return tree[o]; 
    int mid=(l+r)>>1;
    if(b<=mid)//查询区间全在左儿子 
        return query(o<<1,l,mid,a,b);
    else    if(a>mid)//查询区间全在右儿子 
        return query(o<<1|1,mid+1,r,a,b);
    else//左右儿子均有，需把左右儿子组合起来更新，再返回
    {
        node res,res1,res2;
        res1=query(o<<1,l,mid,a,b);
        res2=query(o<<1|1,mid+1,r,a,b);
        res.sum=res1.sum+res2.sum;
        res.left=max(res1.left,res1.sum+res2.left);
        res.right=max(res2.right,res2.sum+res1.right);
        res.maxv=max(res1.right+res2.left,max(res1.maxv,res2.maxv));
        return res;
    }
}
int main()
{
    int x,op,a,b;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>x;
        change(1,1,n,i,x);
    }
    while(m--)
    {
        cin>>op>>a>>b;
        if(op==1)
        {
            if(a>b)
                swap(a,b);
            printf("%d\n",query(1,1,n,a,b).maxv);
        }
        else
            change(1,1,n,a,b);
    }
    return 0;
}