01背包问题dp数组理解dp[i][j-w]
发布时间:2024年01月16日
一、01背包是什么?
有 n 件物品和一个最多能背重量为 w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。
每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
0 1就表示物品的两种状态(0:不放进去,1:放进背包)
二、例子
现有一个背包最大容量为4
现有如下物品:
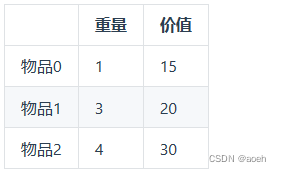
问背包能装下的最大价值是多少?
三、解决思路dp(动态规划)
动规五部曲
1.确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式
dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
之前一直不理解j-weight ,后面想明白,这一个草住主要是为了保证 j > weight,确保背包的容量能放进物品 i 。
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3.dp数组如何初始化
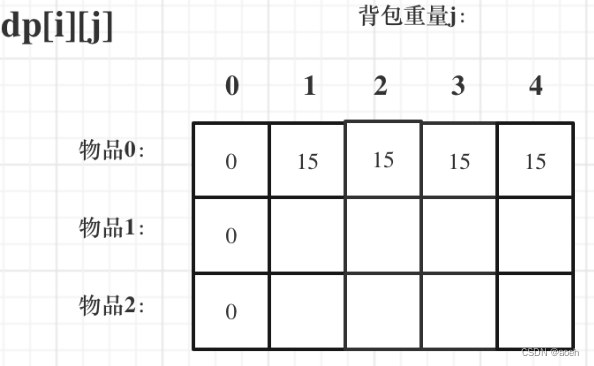
4.确定遍历顺序
先遍历 物品还是先遍历背包重量呢?
其实都可以
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
5.举例推导dp数组
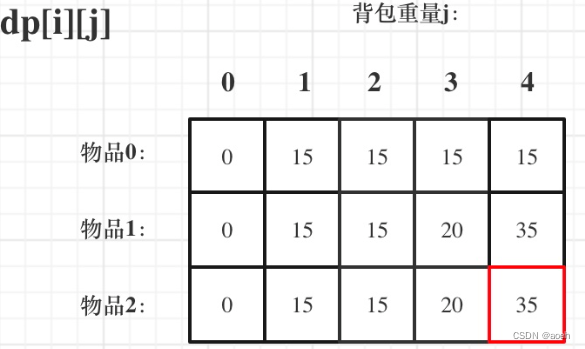
文章来源:https://blog.csdn.net/weixin_43821215/article/details/135630562
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!