浮点数详解

目录

1.概述

2.浮点数的编码方式

2.1.float类型的IEEE编码

2.2.double类型的IEEE编码

2.3.现场问题

2.4.总结

?

---

1.概述

????????计算机也需要运算和存储数学中的实数。在计算机的发展过程中，曾产生过多种存储实数的方式，有的现在已经很少使用了。不管如何存储，都可以将其划分为定点实数存储方式和浮点实数存储方式两种。所谓定点实数，就是约定整数位和小数位的长度，比如用4字节存储实数，我们可以约定两个高字节存放整数部分，两个低字节存储小数部分。这样做的好处是计算效率高，缺点也显而易见：存储不灵活，比如我们想存储65536.5，由于整数的表达范围超过了2字节，就无法用定点实数存储方式了。对应地，也有浮点实数存储方式，道理很简单，就是用一部分二进制位存放小数点的位置信息，我们可以称之为“指数域”，其他的数据位用来存储没有小数点时的数据和符号，我们可以称之为"数据域" "符号域"。在访问时取得指数域，与数据域运算后得到真值，如67.625，利用浮点实数存储方式，数据域可以记录为67625，小数点的位置可以记为10的-3次方，对该数进行访问时计算一下即可。浮点实数存储方式的优缺点和定点实数存储方式的正好相反。在80286之前，程序员常常为实数的计算伤脑筋，而后来出现的浮点协处理器，可以协助主处理器分担浮点运算程序员计算实数的效率因此得到提升，于是浮点实数存储方式也就普及开来，成为现在主流的实数存储方式。但是，在一些条件恶劣的嵌入式开发场合，仍可看到定点实数的存储和使用。
????????在 C/C++中，使用浮点方式存储实数，用两种数据类型来保存浮点数: foat(单精度)和double(双精度)。float在内存中占4字节，double在内存中占8字节。由于占用空间大，double可描述的精度更高。这两种数据类型在内存中同样以十六进制方式存铺,但写大类型有所不同。
????????整型类型是将十进制转换成二进制保存在内存中，以十六进制方式显示。浮点类型并不是将一个浮点小数直接转换成二进制数保存，而是将浮点小数转换成的二进制码重新编码，再进行存储。C/C++的浮点数是有符号的。
????????在C/C++中，将浮点数强制转换为整数时，不会采用数学上四舍五人的方式，而是食弃掉小数部分，不会进位。
????????浮点数的操作不会用到通用寄存器，而是会使用浮点协处理器的浮点寄存器,专门对浮点数进行运算处理。

2.浮点数的编码方式

????????浮点数编码转换采用的是IEEE 规定的编码标准，float 和 double 这两种类型数据的转换原理相同，但由于表示的范围不一样，编码方式有些许区别。IEEE规定的浮点数编码会将一个浮点数转换为二进制数。以科学记数法划分，将浮点数拆分为3部分:符号、指数、尾数。

2.1.float类型的IEEE编码

????????foat类型在内存中占4字节(32位)。最高位用于表示符号，在剩余的31位中，从左向右取8位表示指数，其余表示尾数，如下图所示。

????????在进行二进制转换前，需要对单精度浮点数进行科学记数法转换。例如，将foat类型的12.25f转换为IEEE编码，须将12.25f转换成对应的二进制数1100.01，整数部分为1100，小数部分为01;小数点向左移动，每移动1次，指数加1，移动到除符号位的最高位为1处，停止移动，这里移动3次。对12.25f进行科学记数法转换后二进制部分为1.10001，指数部分为 3。在IEEE 编码中，由于在二进制情况下，最高位始终为1,为一个恒定值，故将其忽略不计。这里是一个正数，所以符号位添加0。
????????12.25f经 IEEE 转换后各位如下。
????????1）符号位：0
????????2）指数位:十进制 3+127=130，转换为二进制为10000010。
????????3）尾数位:10001000000000000000000(当不足23位时，低位补0填)。

????????由于尾数位中最高位1是固定值，故忽略不计，只要在转换回十进制数时加1即可。为什么指数位要加 127呢?这是因为指数可能出现负数，十进制数 127 可表示为二进制数01111111，IEEE编码方式规定，当指数小于0111111时为一个负数，反之为正数，因01111111为0。
????????将示例中转换后的符号位、指数位和尾数位按二进制拼接在一起，就成为一个完整的IEEE 浮点编码:01000001010001000000000000000000。转换成十六进制数为0x41440000内存中以小尾方式进行排列，故为 00004441，分析结果如下图所示。?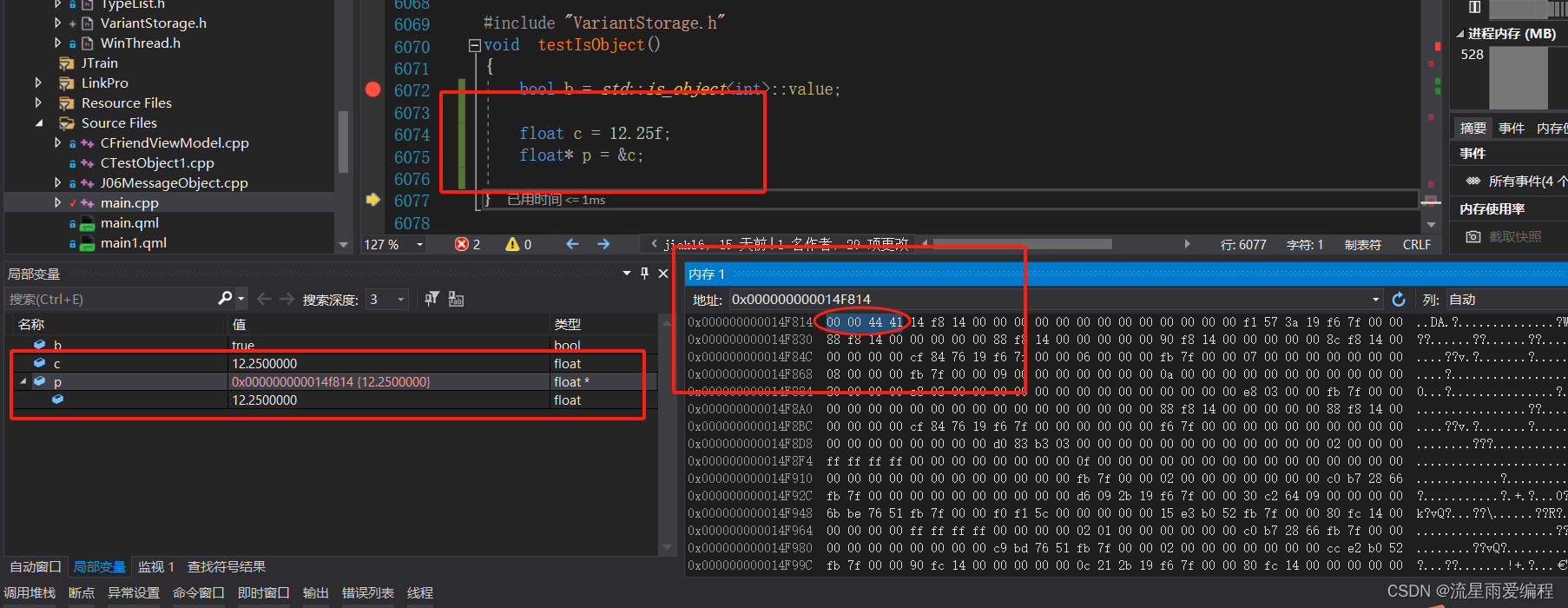

? ? ? ? 使用第三方工具软件计算更清楚，如下图所示：

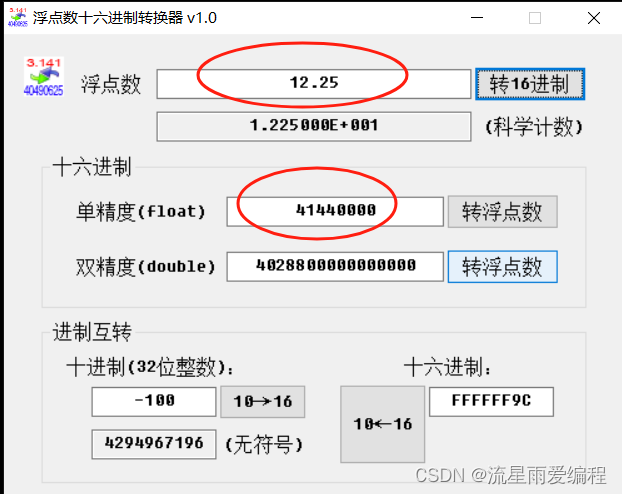
????????上面演示了符号位为正、指数位也为正的情况。那么什么情况下指数位可以为负呢?根据科学记数法，小数点向整数部分移动时，指数做加法。相反，小数点向小数部分移动时，指数需要以0起始做减法。浮点数-0.125f转换EEE编码后，将会是一个符号位为1、指数部分为负的数。-0.125f经转换后二进制部分为0.001，用科学记数法表示为1.0，指数为 -3。
????????-0.125fIEEE 转换后各位的情况如下。
????????1）符号位:1。
????????2）指数位:十进制 127+(-3 )，转换为二进制是 01111100，如果不足8位，则高位补 0。
????????3）尾数位:00000000000000000000000。

????????-0.125f转换后的 IEEE 编码二进制拼接为 10111110000000000000000000000000。转换成十六进制数为 0xBE000000，内存中显示为00 00 00 BE，分析结果如下图所示。

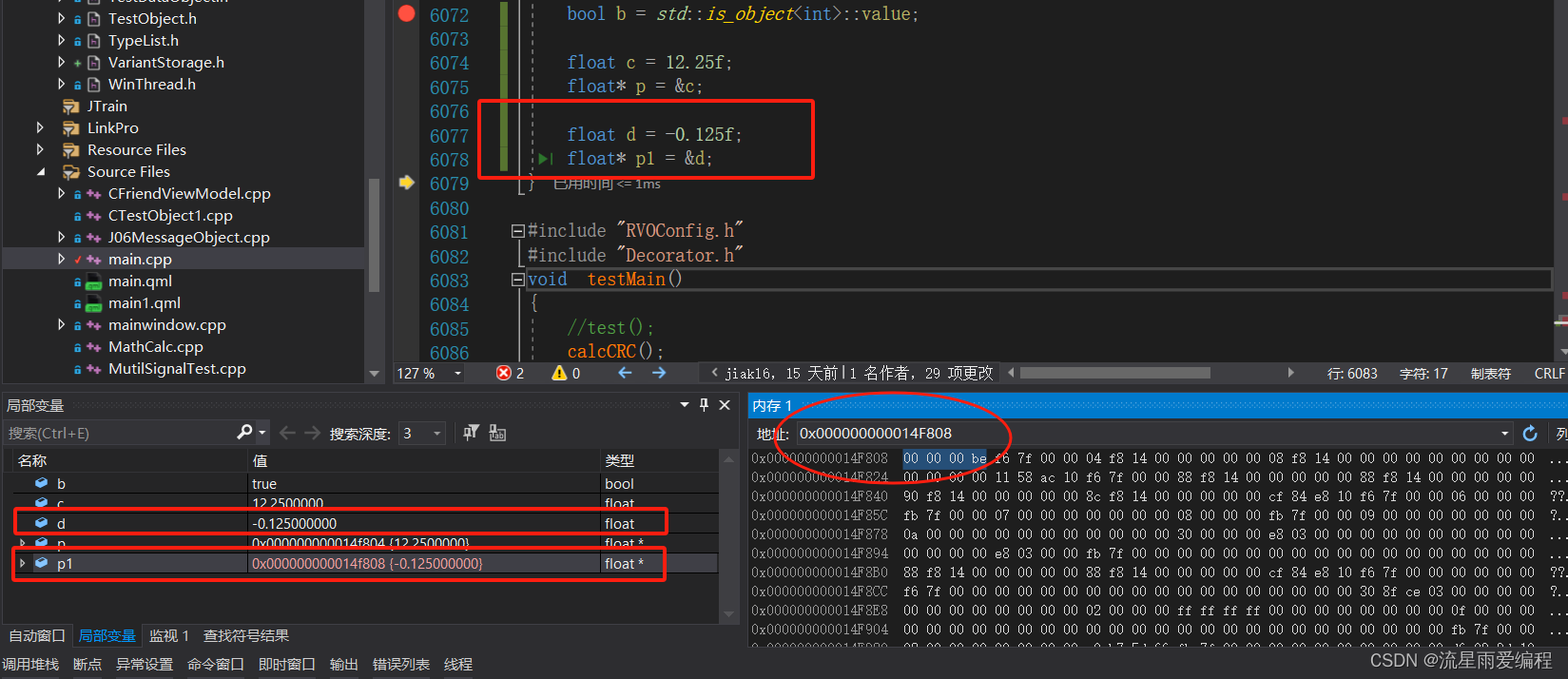
? ? ? ? 使用第三方工具软件计算更清楚，如下图所示：?

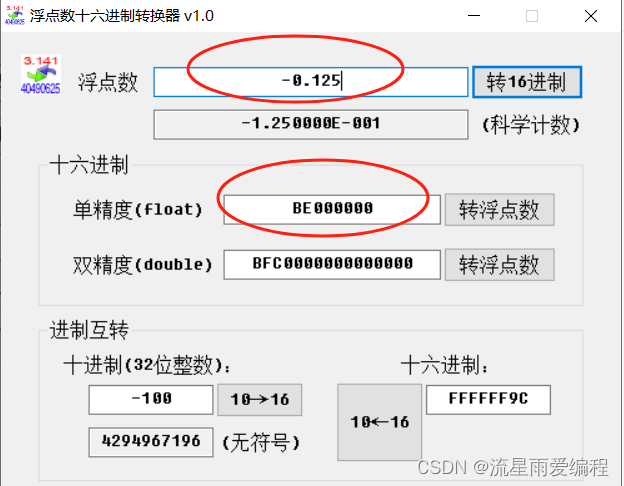
????????上面的两个浮点数小数部分转换为二进制时都是有穷的，如果小数部分转换为二进时得到一个无穷值，则会根据尾数部分的长度舍弃多余的部分。如单精度浮点数1.3f,数部分转换为二进制就会产生无穷值，依次转换为0.3、0.6、1.2、0.4、0.8、1.6、1.2、00.8……转换后得到的二进制数为 1.01001100110011001100110，到第23 位终止，尾数部分无法保存更大的值。

????????1.3f经 EEE 转换后各位的情况如下：
????????1）符号位:0。
????????2）指数位:十进制 0+127，转换二进制01111111。
????????3）尾数位:01001100110011001100110。

????????1.3f转换后的IEEE编码二进制拼接为00111111101001100110011001100110。转换十六进制数为0x3FA66666，在内存中显示为66 66 A6 3F。由于在转换二进制过程中产些了无穷值，舍弃了部分位数，所以进行IEEE编码转换后得到的是一个近似值，存在一定的误差。再次将这个IEEE编码值转换成十进制小数，得到的值为12516582，四合五人保留位小数之后为1.3。这就解释了为什么C++在比较浮点数值是否为0时，要做一个区同中较而不是直接进行等值比较。正确浮点数比较如下代码：

float f1=0.0001f;
if(f2 >=-f1 6& f2 <= f1)
{
    // f1等于0
}

2.2.double类型的IEEE编码

????????前文讲解了单精度浮点类型的IEEE编码。double类型和 foat类型大同小异，只是double类型表示的范围更大，占用空间更多，是 foat类型所占空间的两倍。当然,精准度double 类型占8字节的内存空间，同样，最高位也用于表示符号，指数位占11位，剩也会更高。
????????在 float类型中，指数位范围用8位表示，加127后用于判断指数符号。在double类型余 52 位表示位数。中，由于扩大了精度，因此指数范围使用11位正数表示，加1023 后可用于指数符号判断。double 类型的 IEEE 编码转换过程与 foat 类型一样，读者可根据 foat类型的转换流程来转换 double类型，此处不再赘述。

2.3.现场问题

? ? ? ? 通过上面的讲解，我们知道浮点数是有可能出现经过IEEE编码转换后得到的是一个近似值，跟实际值存在一定的偏差。项目前期制定的设备两端通信协议设计某些字段为double类型，导致采集数据设备采集到的两端的二进制数据不一致的问题。后期调整，全部把double类型的数据转换为整数进行传输，才保证了两端二进制数据的一致性。

2.4.总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注本博客的其它内容。

?