决策树：理解机器学习中的关键算法

决策树：理解机器学习中的关键算法

决策树是一种流行而强大的机器学习算法，它从数据中学习并模拟决策过程，以便对新的未知数据做出预测。由于其直观性和易理解性，决策树成为了分类和回归任务中的首选算法之一。在本文中，我们将深入探讨决策树的工作原理、如何构建决策树、它们的优缺点，以及在现实世界中的应用。

树模型

决策树：从根节点开始一步步走到叶子节点（决策）

所有的数据最终都会落到叶子节点，既可以做分类也可以做回归

例子：一个家庭里面找出玩游戏的人（通过年龄和性别两个特征）

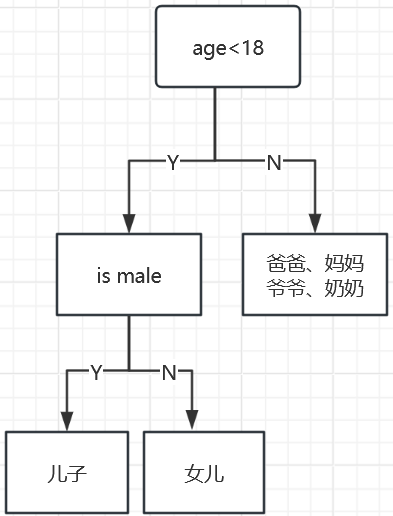
如何切分特征（选择节点）

问题：根节点的特征该用哪个特征？如何切分？

假设：我们目标应该是根节点就像一个老大一样能够更好的切分数据（分类的效果更好），根节点下面的节点自然就是二当家。

目标：通过一种衡量指标，来计算通过不同特征进行分支选择后的分类情况，找出最好的那个当成根节点，以此类推。

衡量指标——熵

熵：表示随机变量不确定性的度量（说白了就是物体内部的混乱程度，熵的值越高，物体的混乱程度越高）

公式：

树的组成

根节点：第一个选择点

非叶子节点与分支：中间过程

叶子节点：最终的决策过程

决策树的基本原理

决策树通过一系列问题将数据集分割成越来越小的子集，最终达到一个可以做出预测的点。每个问题都基于特征和特征值，并且将数据集分割成两个或更多的同质子集，这些子集在目标变量上具有更高的纯度。

构建决策树的步骤

1. 选择最佳特征：选择最佳分割特征是通过计算每个特征的信息增益（Information Gain）或基尼不纯度（Gini Impurity）来决定的。

2. 分割数据：使用上一步选定的特征，将数据集分割成子集。分割可以基于一个阈值（用于连续特征）或特征的分类。

3. 重复分割过程：在每个子集上重复步骤1和步骤2，直到每个子集达到一个停止标准（比如所有的记录都属于同一个类别，或者达到了树的最大深度）。

4. 剪枝：为了避免过拟合，通过剪掉那些对模型预测能力提升不大的分支来简化决策树。

决策树的优点

• 直观易懂：决策树的结构清晰，易于理解和解释，它们的决策规则可以直观地展示出来。

• 不需要很多数据预处理：不需要标准化或归一化数据，也不需要处理缺失值。

• 可以处理非线性关系：由于分割过程的非参数性质，决策树能够捕捉到数据中的非线性关系。

• 多功能性：既可以处理分类问题，也可以处理回归问题。

决策树的缺点

• 容易过拟合：决策树可能会创建过于复杂的树结构，完美地匹配训练数据，但对新数据的泛化能力差。

• 稳定性较差：小的数据变动可能导致生成完全不同的树。

• 偏向于多类别的特征：使用信息增益作为分割标准时，决策树倾向于选择那些具有更多类别的特征。

应用实例

决策树广泛应用于各种领域，如医疗诊断、信用评分、股票市场分析、农业研究等。它们的直观性使得非专业人士也能够理解模型的预测结果。

结论

决策树由于其简单和有效性，在解决分类和回归问题上是一个不可或缺的工具。虽然单独的决策树可能容易过拟合，但通过组合多个决策树构成的集成方法，如随机森林和梯度提升决策树，可以大大提高模型的准确性和鲁棒性。学习和掌握决策树不仅有助于理解基本的机器学习原理，还为进一步探索更复杂的算法奠定了基础。