SegDiff：Image Segmentation with Diffusion Probabilistic Models

SegDiff:基于扩散概率模型的图像分割

摘要：

扩散概率方法用于最先进的图像生成。在这项工作中，我们提出了一种方法来扩展这样的模型来执行图像分割。该方法端到端学习，不依赖于预先训练的主干。输入图像中的信息和当前分割图估计中的信息通过对两个编码器的输出求和来合并。然后，使用扩散模型，使用额外的编码层和解码器来迭代地细化分割图。由于扩散模型是概率性的，因此可以多次应用，并将结果合并到最终的分割图中。新方法在城市景观验证集、Vaihingen建筑分割基准和MoNuSeg数据集上产生最先进的结果。

1 介绍

扩散方法迭代改进给定图像，获得的图像质量与其他类型的生成模型相当或优于其他类型的生成模型，包括其他形式的对数似然模型和对抗模型[10,19]。这种方法已被证明在许多有条件和无条件的生成任务中表现优异。

绝大多数扩散模型应用于没有绝对基础真值结果的领域，并且通过用户研究或使用几个质量和多样性分数来评估输出。据我们所知，除了超分辨率[19,27,41]外，扩散模型还没有被应用到地面真值结果唯一的问题中。在这项工作中，我们解决了图像分割问题。这个问题是经典计算机视觉和过去十年深度学习方法的基石。这一领域的领先方法不同架构的编码器-解码器网[4,31,38,50,52,53]。虽然已经尝试了对抗性方法[12,33,49,51]，但它们并不构成当前的技术水平。

因此，主要用于类gan生成任务的扩散模型是否在该领域具有竞争力尚不确定。在这项工作中，我们提出应用扩散模型来学习图像分割映射。与最近在图像分割领域的其他改进不同[13,22,44]，我们端到端训练我们的方法，而不依赖于预训练的骨干网络。

扩散模型仅通过将该信息与当前估计xt产生的信息聚合在一起的总和来使用以输入图像为条件的去噪网络。具体来说，输入图像I和二值分割图的当前估计xt通过两个不同的编码器，这些多通道张量的和通过U-Net传递[38]，以提供下一个估计xt?1。

由于生成过程在本质上是随机的，因此可以得到多个解。正如我们所展示的，合并这些解决方案，通过简单地计算多次运行的平均值，可以提高总体精度。

提出的新方法在多个基准上产生了最先进的结果:城市景观[9]、建筑分割[39]和核分割[25,26]。

我们的主要贡献是:

我们率先将扩散模型应用于图像分割问题。

我们提出了一种新的方法来调节输入图像上的模型。

?我们引入了多代的概念，以提高扩散模型的性能和校准。

我们在多个基准测试中获得了最先进的结果。对于小的数据集，余量特别大。

2 相关工作

图像分割：

是为每个像素分配一个标签的问题，该标签标识它是否属于特定的类。使用不同的体系结构对这个问题进行了广泛的研究。这些包括全卷积网络[31]，具有跳过连接的编码器-解码器体系结构，如U-Net[38]，基于变压器的体系结构，如segformer[50]，甚至结合超网络的体系结构，如[36]。

扩散概率模型(DPM) [43]：

是一类基于马尔可夫链的生成模型，它可以将简单分布(例如高斯分布)转换为在复杂分布中采样的数据。扩散模型能够生成高质量的图像，可以与最新的GAN方法竞争，甚至优于GAN方法[10,18,35,43]。Huang等人[21]引入了扩散模型似然估计的变分框架。随后，Kingma等人[23]提出了一种V变量扩散模型，该模型在图像密度的似然估计中产生了最先进的结果。扩散模型也被应用于语言建模[2,20]，其中使用了一种新的分类数据扩散模型。

条件扩散概率模型

在我们的工作中，我们使用扩散模型作为条件生成来解决给定图像的图像分割问题。扩散模型的条件生成包括类条件生成方法，这是通过在时间戳嵌入中添加类嵌入来获得的[35]。[8]中提出了一种指导DDPM生成过程的方法。这种方法允许基于给定的参考图像生成图像，而无需任何额外的学习。

在超分辨率领域，对低分辨率图像进行上采样，然后在每次迭代时将低分辨率图像以通道方式拼接到生成的图像中[19,41]。类似的方法是在拼接之前将低分辨率图像通过卷积块[27]。与我们的工作同时，扩散模型被应用于图像到图像的翻译任务[40]。这些任务包括裁剪、上漆和上色。所得结果优于强GAN基线。

条件扩散模型也被用于语音生成。用卷积网络处理梅尔谱图，并将其用作DPM去噪网络的附加输入。[6,24,30]。此外，在[37]中引入了文本到语音的扩散模型，该模型将文本作为扩散模型的条件。

在我们的工作中，我们采用了一种不同的方法来调节，在输入图像经过卷积编码器后，将其添加(而不是串联)到当前分割图像的估计中。换句话说，我们学习残差模型的DPM。

3 背景

我们简要介绍[18]中提到的扩散模型的公式。扩散模型是一种用马尔可夫链参数化的生成模型，由正向和反向过程组成。正向过程q用公式描述:

式中，T为扩散模型的步数，x1，…， xT是潜在变量，x0是数据中的样本。在正演过程的每一次迭代中，根据

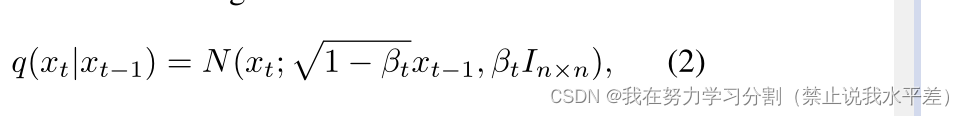
式中，βt是定义附加噪声调度的常数，In×n是大小为n的单位矩阵。如[18]所示，

转发过程支持在任意时间戳t上采样，公式如下

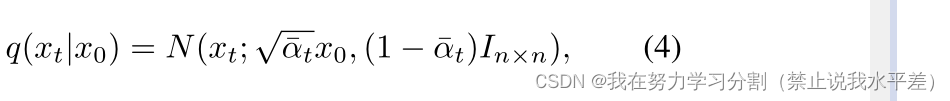
可以重新参数化为:

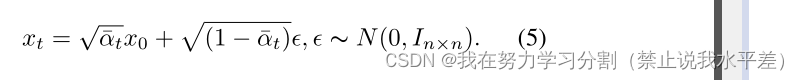
逆过程参数化为θ，定义为

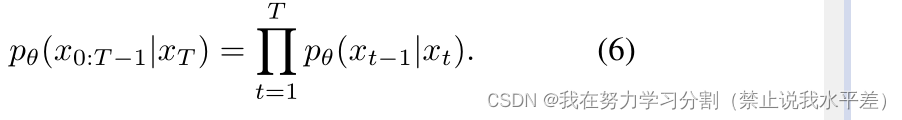
从pθ(xT) = N(xT;0, In×n)，反向过程将潜在变量分布pθ(xT)转换为数据分布pθ(x0)。相反的过程步骤是通过采用小的高斯步骤来完成的

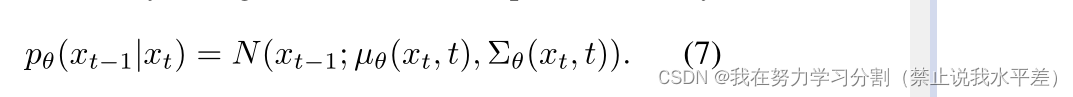
利用贝叶斯定理计算q(xt?1|xt, x0)，得到:

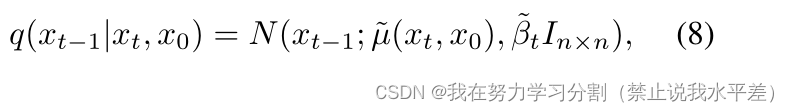
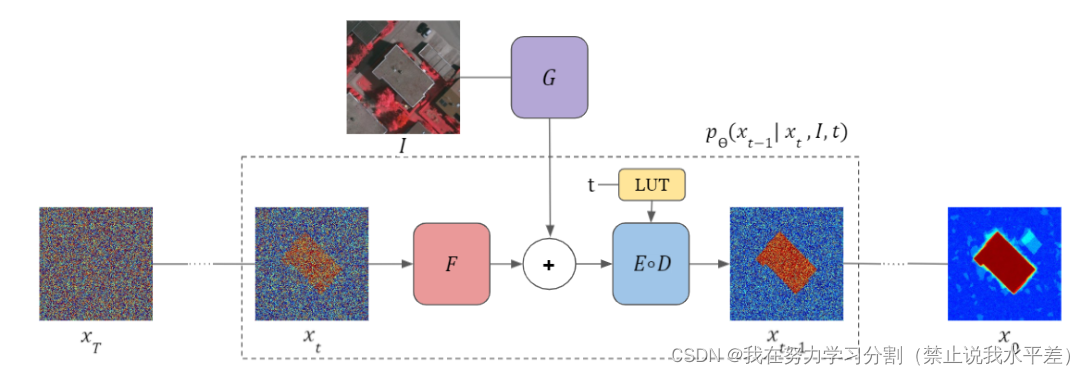
图1所示。我们提出的图像分割扩散方法用F对输入信号xt进行编码。将提取的特征与网络g生成的条件图像I的特征图进行求和。网络E和D分别是U-net编码器和解码器[35,38]，对估计的分割图进行细化，得到xt?1。

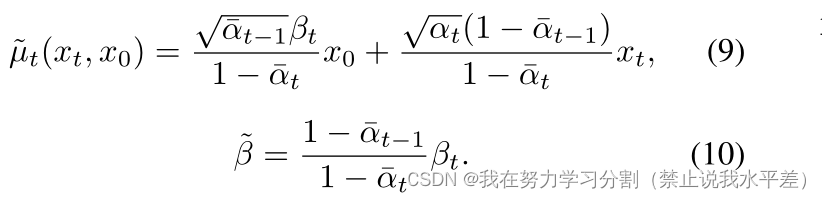
神经网络μθ预测噪声?，用Eq. 5,9对噪声进行参数化，得到:

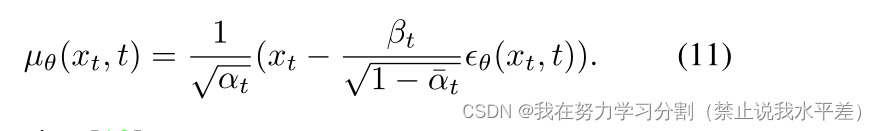
如下[18]所示：

选择前向过程方差参数为从β1 = 10?4到βT = 2 * 10?2的线性递增常数，形式为:

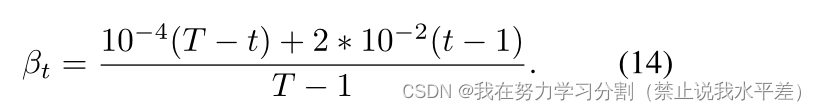
最后，我们将最小化这项

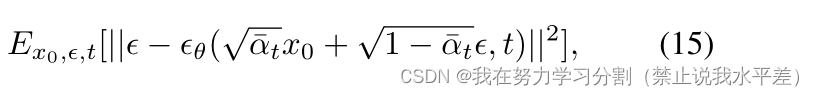
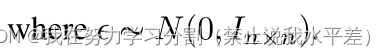
对于推理，我们可以用Eq. 11重新参数化反向过程Eq. 7，得到

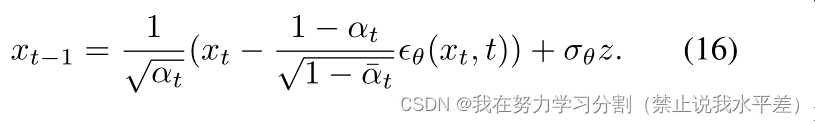
4. 方法

我们的方法通过在输入张量上设置阶跃估计函数?θ来修改扩散模型

结合了从当前估计值xt和输入图像I中得到的信息。

在扩散模型中，θ是典型的U-Net[38]。在我们的工作中，θ可以表示为:

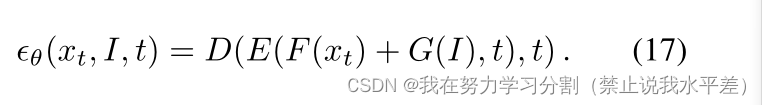
在这个架构中，U-Net的解码器D是常规的，它的编码器被分解成三个网络:E、F和g。最后一个网络编码输入图像，而F编码当前步骤xt的分割图。两个处理后的输入具有相同的空间维度和通道数量。基于剩余连接的成功[17]，我们将这些信号相加F (xt) + G(I)。这个和然后传递给U-Net编码器E的其余部分。

当前步骤索引t被传递到两个不同的网络D和e。在每个网络中，它都使用共享学习查找表嵌入。

Eq. 17的?θ输出以I为条件，插入Eq. 16，取代无条件的?θ网络。由此产生的推理时间过程如图1所示，并在图1中详细说明。

4.1 多次迭代？

由于在推理过程中计算xt?1包括添加σθ(xt, t)z，其中z来自标准分布，因此在相同输入的推理方法的不同运行之间存在显着的可变性，见图2(b)。为了利用这种现象，我们多次运行推理算法，然后对结果进行平均。通过这种方式，我们稳定了分割结果，提高了性能，如图2(c)所示。我们在所有实验中使用了30个生成的实例，除了消融研究中的实验，它量化了该平均过程的增益。

4.2 训练

训练过程如图2所示。扩散步数T由用户设定。对于每次迭代，得到一个随机样本(Ii, Mi)(图像及其相关联的地真二值分割图)。迭代次数1≤t≤t从均匀分布中采样，从标准分布中采样。然后我们根据Eq. 5对xt进行采样，计算F (xt) + G(Ii)，并应用网络E和D得到?θ(xt, Ii, t)。

最小化的损失是Eq 15的修改版本，即:

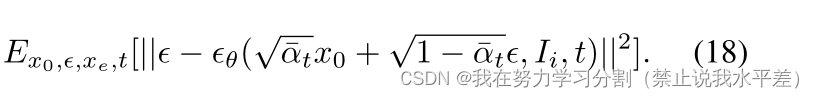
在训练时，输入图像Ii的ground truth segmentation是已知的，通过设x0 = Mi来计算损失。

4.3 体系结构

输入图像编码器G是由残差密集块中的残差[47](Residual in Residual Dense Blocks, rrdb)构建而成的，rrdb结合了多级残差连接，没有批处理归一化层。G有一个输入2d -卷积层，一个周围有残余连接的RRDB，然后是另一个2d -卷积层，漏RELU激活和最后一个2d -卷积输出层。F是一个2卷积层，具有单通道输入和C通道输出。

θ的编解码器部分，即D和E，基于U-Net，类似于[35]。每个级别都由残差块组成，在分辨率为16x16和8x8的情况下，每个残差块后面都有一个注意层。瓶颈包含两个剩余块，中间有一个注意层。每个注意层包含多个注意头。

残差块由两个卷积块组成，每个卷积块包含群范数、Silu激活和一个2d -卷积层。残差块通过一个线性层、四路激活和另一个线性层来接收时间嵌入。然后将结果添加到第一个2d卷积块的输出中。

此外，残留块具有传递其所有内容的残留连接。

在编码器侧(网络E)，在相同深度的残差块之后有一个下采样块，这是一个步幅为2的2d -卷积层。在解码器侧(网络D)，在相同深度的残差块之后有一个上样块，该上样块由距离最近的使空间大小加倍的插值组成，然后是一个2d -卷积层。编码器中的每一层都有一个到解码器端的跳过连接。

5 实验

我们提出了三个数据集的分割结果，以及消融研究。cityscape数据集[9]是一个实例分割数据集，包含5,000个带注释的图像，分为2,975张用于训练，500张用于验证，1,525张用于测试。

所使用的实验设置有时被称为交互式分割，其动机是需要加速对象注释[1]。在此设置下，有8个对象类别，目标是恢复对象的逐像素蒙版，给定一个裁剪的补丁，其中包含每个对象周围的边界框。

我们的每对象训练和验证集是通过使用地面真值类的位置从原始cityscape集中的图像中提取作物来创建的(我们无法访问原始cityscape测试集的地面真值标签)。

图2。获得cityscape, vaihingen和MoNuSeg的多个分割结果。(a)输入图像，(b)在同一输入上多次运行获得的结果的子集，通过蓝色0到红色1之间的喷流颜色刻度可视化，(c)平均结果，(d)地面真值。

我们将cityscape数据集的方法与PSPDeepLab[5]、Polygon-RNN++[1]、CurveGCN[29]、深度活动轮廓[14]、Segformer-B5[50]和Stdc1[11]进行了比较。对于大多数基线，我们报告了从以前的出版物中获得的结果。对于Segformer和Stdc，我们从头开始训练。

我们没有与PolyTrans-进行比较表单[28]，因为它使用不同的协议。具体来说，这种方法在Mask R-CNN[16]的基础上进行了改进，它利用整个图像(而不仅仅是分割补丁)作为其输入的一部分，并且不能以一种能够进行直接比较的方式在标准补丁上工作。

V aihingen数据集[39]包含德国V aihingen的168张航空图像，分为100张图像用于train-

8分，68分。任务是在每个图像中分割中心建筑。对于该数据集，领先的基线是DSAC[34]、DarNet[7]、TDAC[15]、Deep active contours[14]、FCN-UNET[38]、FCN-ResNet-34、FCNHarDNet-85[4]、Segformer-B5[50]和Stdc1[11]。

MoNuSeg数据集[25,26]包含一个训练集，其中包含来自7个器官的30张显微图像，带有21,623个单个细胞核的注释。测试数据集包含14个类似的图像。我们将图像调整为512 × 512的分辨率，如下[45]。相关基线方法有FCN[3]、UNET[38]、UNET++[53]、ResUnet[48]、Axial attention (A.A) UNET[46]和Medical transformer[45]。

评估

cityscape数据集使用每个类的平均交叉路口(mIoU)的通用指标进行评估。

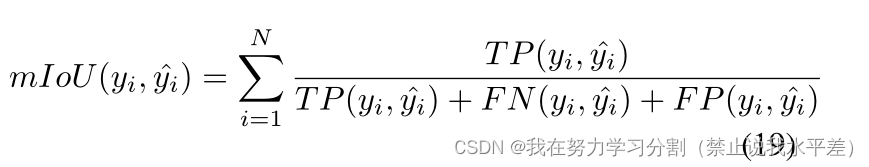
其中N为数据集中的类数，TP为基本真值y与输出掩码y之间的真正，FN为假阴性，FP为假阳性。

V aihingen数据集使用几个指标进行评估:mIoU, f1分数，加权覆盖率(WCov)和边界f分数(BoundF)，如[7]所述。简而言之，如果预测与真实情况的距离在一定范围内，那么预测就是正确的。基准测试使用5个阈值(从1px到5px)来评估性能。

在之前的工作之后，对MoNuSeg数据集的评估使用mIoU和F1-score进行。

训练细节

在以往的研究中，扩散步数为1000步[18]，甚至达到4000步[35]。文献表明越多越好[42]。在我们的主要实验中，我们使用了100个扩散步骤来减少推理时间。另外一组实验研究了扩散步骤数对方法性能和运行时间的影响。

我们所有的实验都使用了AdamW[32]优化器。基于RRDB块越多，结果越好这一直觉，我们在不过度减少批处理大小的情况下使用了尽可能多的块。用于分辨率为256 × 256的数据集的Unet相对于分辨率为一半的数据集有一个额外的层，以便考虑空间维度。

在cityscape数据集上，我们的模型的输入分辨率为128 × 128。测试度量是在原始分辨率上计算的;因此，我们将预测大小调整为原始图像大小。

训练的批量大小为30张图像。该网络有15个RRDB块，深度为6。通道数设置为[C, C, 2C, 2C, 4C, 4C]，其中C = 128。我们采用了与[14]中相同的增强方案，

包括在[0.75,1.25]范围内的随机缩放，每个方向最多22度旋转，以及0.5概率的水平翻转。

对于Vaihingen数据集，输入图像的大小和测试图像的分辨率为256 × 256。实验的批处理大小为8个图像，6个RRDB块，深度为7。通道数设置为[C, C, C, 2C, 2C, 4C, 4C]，其中C = 128。

使用与[7]相同的增强:在[0.75,1.5]范围内均匀采样的因子随机缩放，在0和360度之间均匀采样的旋转，独立的水平和垂直翻转，应用概率为0.5，以及随机颜色抖动，最大值为0.6亮度，0.5对比度，0.4饱和度和0.025色调。

对于MoNuSeg，输入图像分辨率为256×256，但测试分辨率为512 × 512。为了解决这个问题，我们应用了一个256 × 256的滑动窗口，步长为256，也就是说，我们分别测试图像的每个象限。

实验以8张图像的批处理大小进行，其中包含12个RRDB块。网络深度为7，每个深度的通道数为[C, C, C, 2C, 2C, 4C, 4C]，其中C = 128。我们使用与[45]相同的增强方案，随机裁剪256 × 256，以调整GPU内存。

值得注意的是，除了Segformer和Stdf之外，所有基线方法都依赖于在ImageNet、PASCAL或COCO数据集上获得的预训练权重。我们的网络是用随机权重初始化的。

结果

根据之前的工作，cityscape在两种设置中进行评估。紧密:在这种情况下，样本(图像和相关的分割图)是通过物体蒙版周围的紧密裁剪来提取的。扩展:在对象掩模周围进行裁剪，比紧裁剪大15%。该模型的输入量比紧凑模型大10% - 20%。这种设置略具挑战性，因为关于目标对象位置的信息较少。cityscape数据集的结果报告在表1中。可以看到，我们的方法在所有类别和两种设置中都优于所有基线方法。即使对于最新的基线方法，差距也很明显，如图3所示，对于训练图像较少的数据集，性能差距尤其大。vaihingen数据集的结果如表2所示。可以看出，我们的方法在所有四个分数上都优于之前工作报告的结果。MoNuSeg数据集的结果如表3所示。在这两个分割指标中，我们的方法优于之前的所有工作，包括专门为该分割任务开发的U-Net和变压器的最新变体。

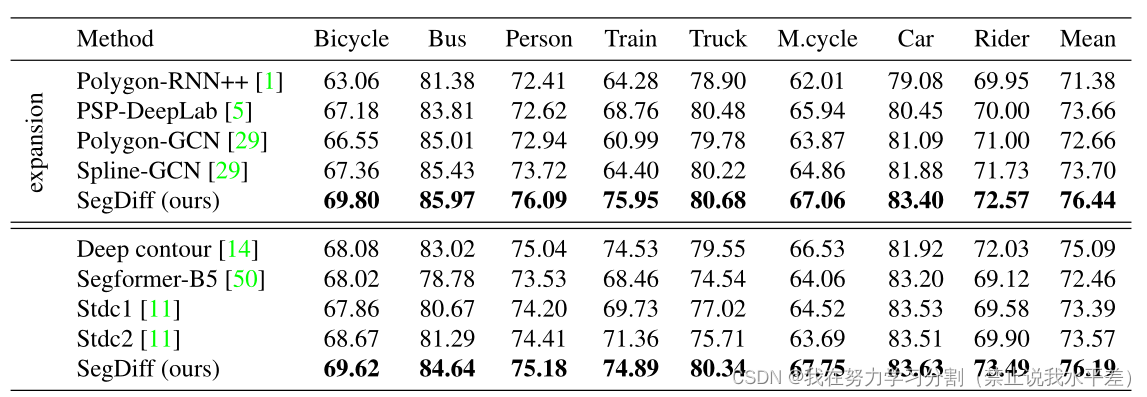
表1。两种方案的城市景观分割结果:顶部为围绕包围框展开15%的分割结果;底部部分为紧边界框的分割结果。

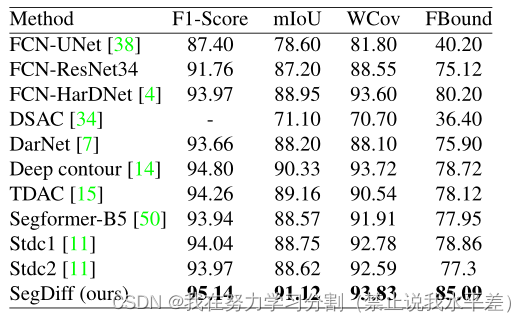
表2。vaihingen数据集的分割结果。

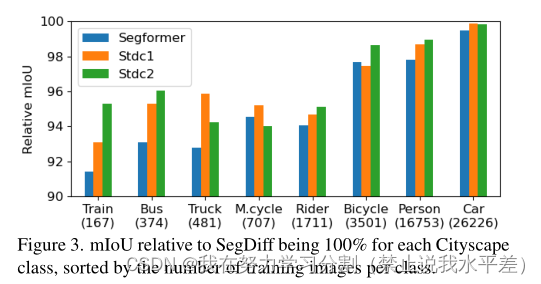
图3。对于每个Cityscape类，相对于SegDiff的mIoU为100%，按每个类的训练图像数量排序。

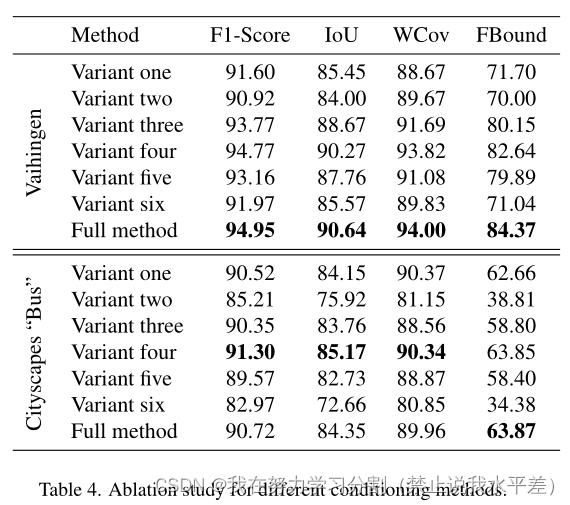
表4。不同调理方法的消融研究。

图4给出了三个数据集的mIoU分割度量作为迭代次数函数的性能。有趣的是，在不同的数据集中，达到最大分数所需的扩散步骤数是不同的。所有cityscape类都表现出类似的行为(具有不同的性能水平)，在第60次迭代时达到饱和。vaihingen分数需要更长的时间才能达到最大值。虽然人们可能将其归因于网络观察到的更大的输入图像大小，但与vaihingen具有相同输入图像大小的MoNuSeg达到了饱和-类似于cityscape类。另一种假设可以将所需的迭代次数与分割掩模内的像素比率联系起来，这对于cityscape和MoNuSeg来说比对于vaihingen更高。这需要进一步的验证。

接下来我们研究了产生在-的数量的影响对业绩的立场。结果如图5所示。一般来说，增加生成实例的数量往往会增加mIoU得分。但是，达到最佳性能所需的运行次数因类而异。例如，对于cityscape的“Bus”和“Train”类，当分别使用10个和3个生成实例时可以获得最佳分数。MoNuSeg，需要相当多的运行(25)来获得最大的性能。另一方面，当生成的实例数量增加时，推理时间也会线性增加，导致与Segformer和Stdc等体系结构相比，方法更慢。通过采用多代实现改进的另一个方面是校准。校准分数是用预测概率与事件真实概率之间的差值来衡量的。例如，一个完美校准的模型定义为P(Y = Y | P = P) = P，这意味着预测概率等于事件的真实概率。我们通过将[0,1]范围分成10个均匀的桶来估计校准分数，然后平均每个桶的平均预测概率与阳性样本百分比之间的平方差。

校正分数的检验结果是预如图6所示。对于大多数数据集，增加生成实例的数量可以提高校准分数，特别是当增加来自单个实例时。此外，对于cityscape中的较大类别(Rider和Bicycle)以及MoNuSeg和vaihingen数据集，与其他数据集相比，改进继续增加。《cityscape》中的“Train”类是个例外;在这里，单实例校准得分优于其他生成实例数量较大的实验。这种现象可能是由于测试图像的大小变化很大，而测试图像的数量很少。

消融研究

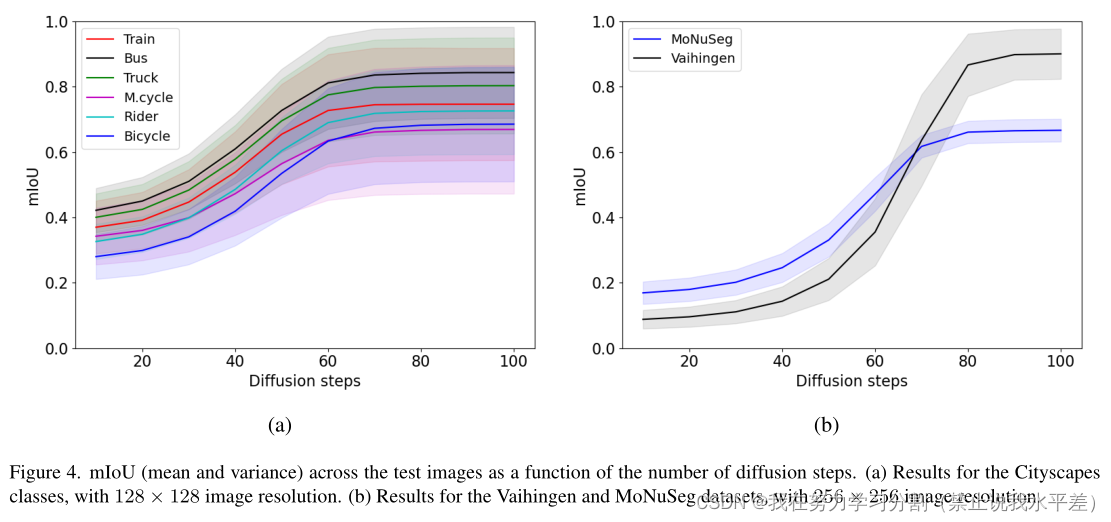
图4。测试图像上的mIoU(均值和方差)作为扩散步骤数的函数。(a) cityscape类的结果，图像分辨率为128 × 128。(b) V aihingen和MoNuSeg数据集的结果，图像分辨率为256 × 256。

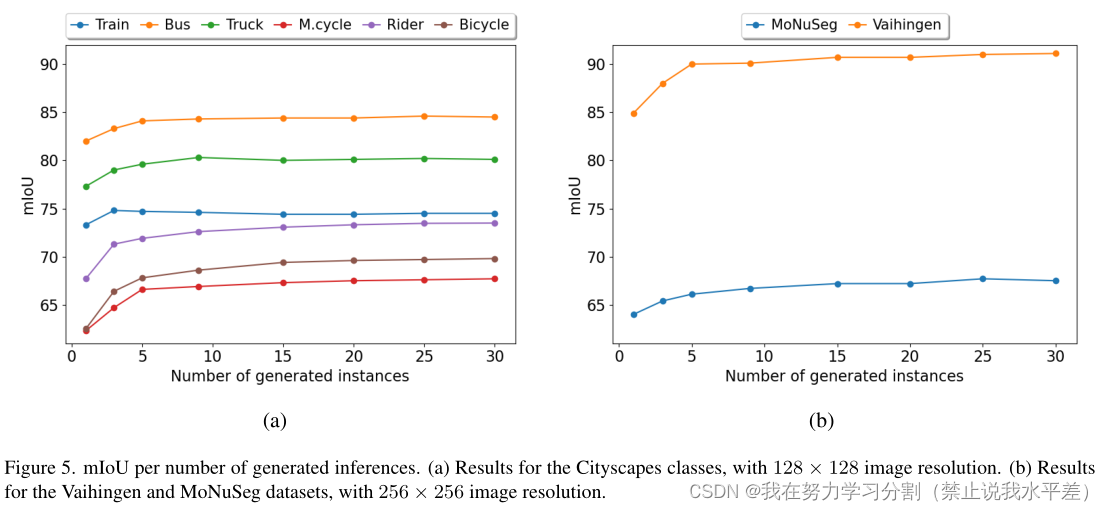
图5。每生成的推论数的mIoU。(a) cityscape类的结果，图像分辨率为128 × 128。(b) V aihingen和MoNuSeg数据集的结果，图像分辨率为256 × 256。

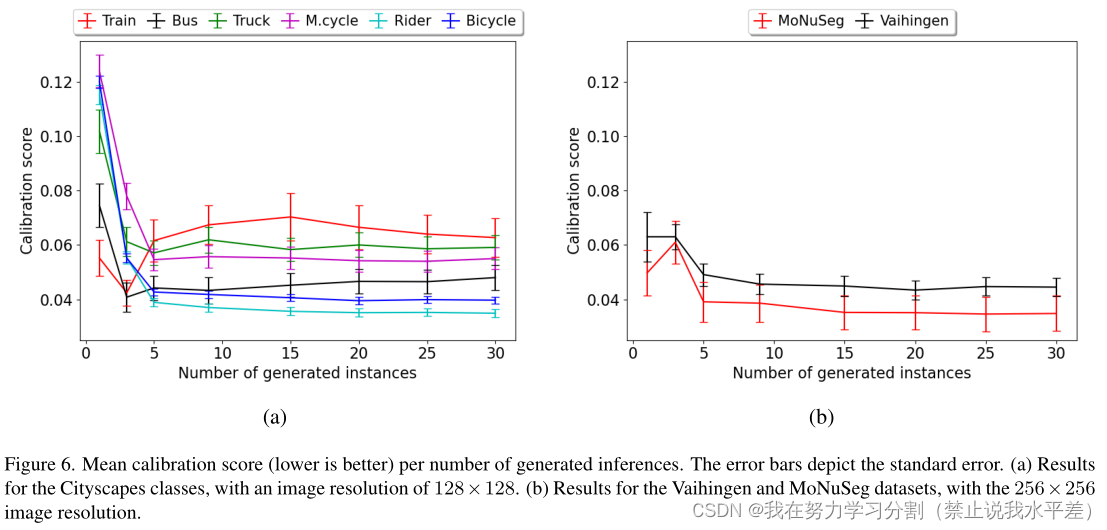
图6。每生成的推论数的平均校准分数(越低越好)。误差条表示标准误差。(a) cityscape类的结果，图像分辨率为128×128。(b) V aihingen和MoNuSeg数据集的结果，图像分辨率为256×256。

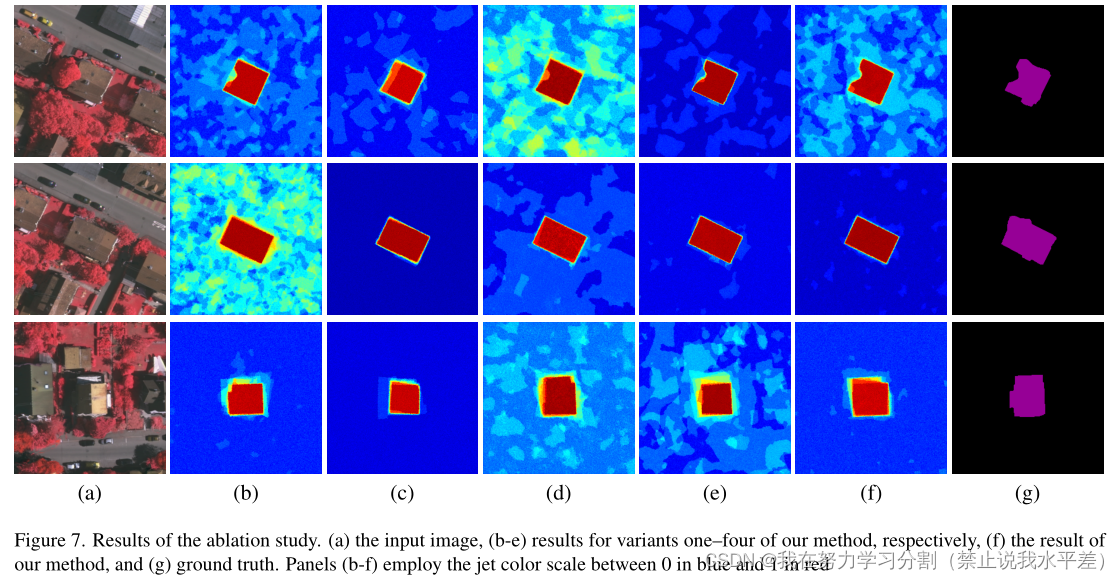
图7。消融研究的结果。(a)输入图像，(b-e)分别为我们的方法的变体1 - 4的结果，(f)我们的方法的结果，和(g)地面真值。面板(b-f)采用介于0(蓝色)和1(红色)之间的喷射色刻度

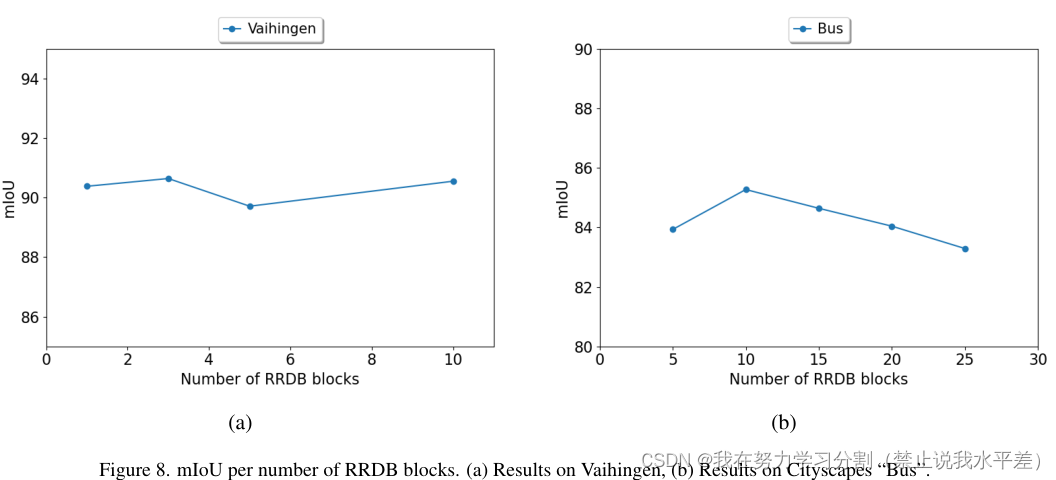
图8。每个RRDB块数的mIoU。(a) vaihingen的结果，(b) cityscape“Bus”的结果。

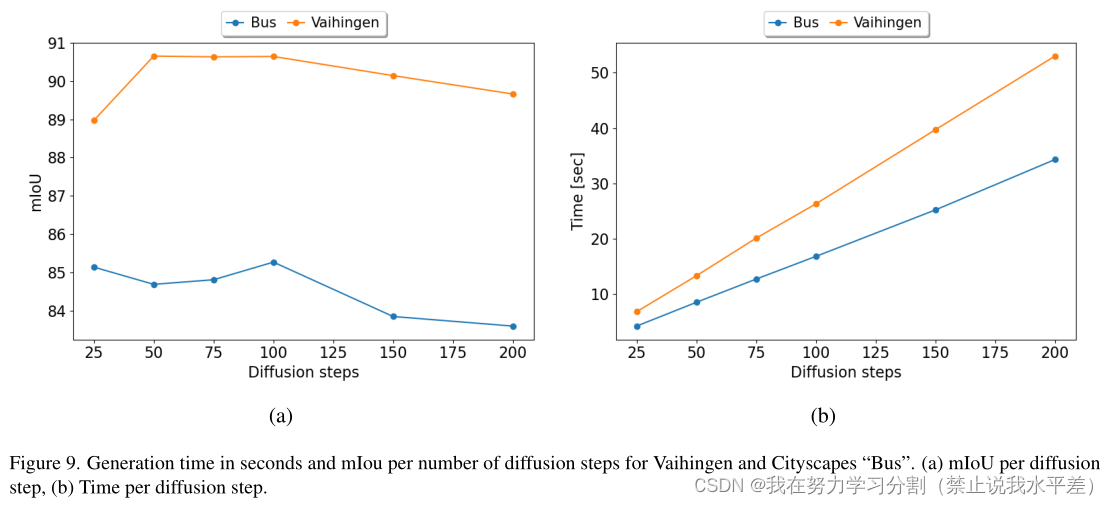
图9。以秒为单位的生成时间和以mIou为单位的扩散步骤为vaihingen和城市景观“巴士”。(a)每个扩散步骤的mIoU， (b)每个扩散步骤的时间。

我们评估了我们方法的各种替代方案。第一种变体在通道维度上连接[F (xt)， G(I)]。第二种改型采用FCHarDNet-70 V2[4]代替rrdb。第三种变体，在[19,41]之后，用-将I以通道方式连接到xt

用编码器输出。最后一种替代方法是通过U-Net模块传播F (xt)，并在第一、第三和第五个下采样块(变体4 - 6)之后将其添加到G(I)中，而不是执行F (xt) + G(I)。在这种变体中，G(I)被下采样以匹配所需的通道数量，方法是将其传播到一个步幅为2的2d卷积层。

通过在V aihingen数据集和cityscape“Bus”上平均9个生成的实例来测试这些变体实验(因此，我们方法报告的性能与表2中报告的性能略有不同)。

作为一种条件反射方法，我们引入的求和方法比vaihinen上的串联(变体一)要好差距很大，而在cityscape的“巴士”上，差距很小。在两个数据集(变体二)中，RRDB块比FCHarDNet架构更可取。删除编码器会显著影响参数(变体三)，对Vaihingen影响更大。变体四的信号积分位置的变化导致Vaihingen上的差异可以忽略不计，甚至优于我们在cityscape“Bus”上的完整方法。随着与第一层的距离增加，变体5和变体6会导致性能下降。图7描述了V aihingen数据集的各种变体(1 - 4)的样本结果。

参数的敏感性

为了测试我们提出的方法的稳定性，我们用两个超参数进行了实验对性能影响最大的参数是:扩散步骤的数量和RRDB块的数量。为了研究这些参数的影响，我们在[25、50、75、100、150、200]范围内改变了扩散步骤的数量，在V aihingen的[1、3、5、10]范围内改变了RRDB块的数量，在Cityscapes“Bus”的[5、10、15、20、25]范围内改变了RRDB块的数量。我们从基线配置开始(100个扩散步骤，Vaihingen的3个RRDB块，cityscape“Bus”的10个RRDB块)，并围绕这些值进行不同的实验。

RRDB块数量的影响

在这一部分中，我们将扩散步骤的数量设置为100。如图8所示，在我们的配置下，Vaihingen的最佳RRDB块数为3，而cityscape“Bus”的最佳RRDB块数为10。然而，很明显，街区的数量对城市景观和万兴根的影响都是有限的。

Vaihingen的最佳和最差性能点之间的差距小于1 mIoU，而cityscape“Bus”的差距小于2 mIoU。因此，我们得出结论，该超参数对性能的影响很小。

改变扩散步数T

在这一部分中，我们将vaihingen的RRDB块数设置为3，将cityscape“Bus”设置为10。我们探讨了关于扩散步骤数量T的可能的精度/运行时权衡。结果如图9所示。

如图9(a)所示，当扩散步数增加时，Vaihingen的图波动小于1 mIoU，而cityscape“Bus”的图波动小于2 mIoU。

令人惊讶的是，当扩散步骤的数量减少时，即使只有25个，与文献[18,35]相比，这是一个非常低的数字，分割结果在两个数据集中都保持稳定，V aihingen的退化仅高达2 mIou，而Cityscapes“Bus”的退化仅为1 mIou。

这种减少可以将性能提高四倍，并为运行时权衡提供合理的准确性。

图9(b)给出了一个样品以秒为单位生成时间的结果。可以观察到，两个图都是线性的，具有不同的斜率。主要原因是图像大小的差异(《V aihingen》是256 × 256，《cityscape》是128 × 128)。另一个次要原因是本实验中RRDB块数量的差异。

6 结论

大量的方法已经应用于图像分割，包括活动轮廓及其深度变体、编码器-解码器架构和U-Nets，它们与最近的基于变压器的方法一起代表了一种领先的方法。在这项工作中，我们建议利用最先进的扩散模型图像生成技术。我们的扩散模型采用U-Net架构，该架构用于增量改进得到的扩散模型

代，类似于其他最近的扩散模型。

为了调节输入图像，我们生成了另一条编码路径，这类似于传统图像分割方法中使用的U-Net编码器和解码器。

通过将U-Net编码器中早期的激活相加，合并了两个编码器路径。

使用我们的方法，我们在各种基准上获得了最先进的分割结果，包括街景图像、航空图像和显微镜。